Data Mining | 二分类模型评估-ROC/AUC/K-S/GINI
1 混淆矩阵衍生指标
上面提到的ACC、PPV、TPR、FPR等指标,都是对某一给定分类结果的评估,而绝大多数模型都能产生好多份分类结果(通过调整阈值),所以它们的评估是单一的、片面的,并不能全面地评估模型的效果。因此,需要引入新的评估指标,来综合全面地评估模型,它们就是如下所述,由混淆矩阵衍生的一系列评估指标。
1.1 ROC
ROC(Receiver Operating Characteristic)曲线,又称受试者工作特征曲线,常用于二分类模型性能的度量,其最大优点是「无视样本不平衡」,即对正负样例占比不敏感。
ROC曲线由两个指标构建而成: TPR(真正例率)与 FPR(假正例率),其中,纵坐标为TPR,横坐标为FPR,下面就是一个标准的ROC曲线图。
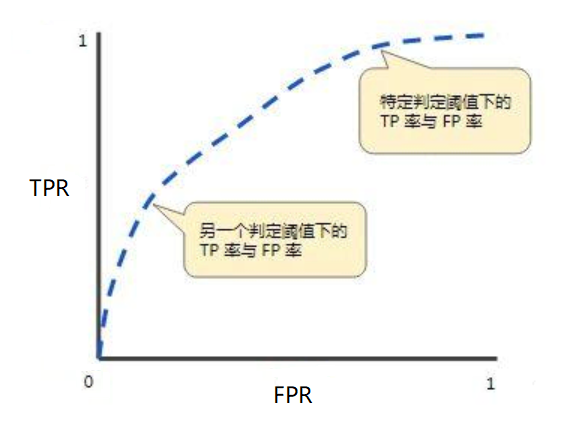
与P-R曲线的绘制类似,ROC曲线也是通过遍历所有阈值来绘制整条曲线的,即ROC曲线上的每一个点,都对应着特定预测阈值下的一对FPR和TPR。以逻辑回归为例,分类器最后会在测试集中输出预测概率P(预测y=1的概率),与测试集中原有真实的y一起,这样就构成了两列数据(如下图)。其中,Cls表示真实的分类,P代表1、N代表0;Score表示对应样本为1的预测概率。
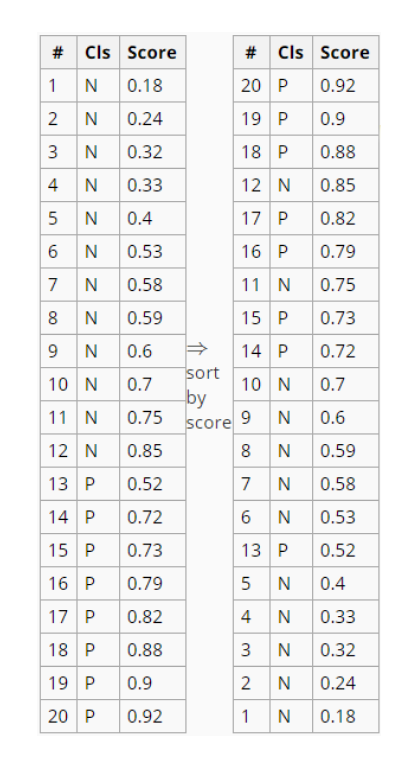
ROC曲线的绘制
- 从上面两列数据出发,对预测概率Score进行降序排列
- 以排序后的预测概率Score为阈值(>=阈值就预测为P),则从上到下每个阈值都对应一列预测的y,根据真实的y和预测的y就能得到一个混淆矩阵,进而能计算出相应的TPR与FPR。所以,每一个阈值,都对应一列预测的y,对应一个混淆矩阵,对应一对TPR与FPR
- 以TPR为纵轴、FPR为横轴,把不同阈值对应的(FPR,TPR)在坐标轴中画出来并连接成曲线,这条曲线就是ROC曲线
经过如上过程就能绘制出ROC曲线。并且,如果我们不断的遍历所有阈值,预测的正样本和负样本会不断变化,ROC曲线会越来越平滑。
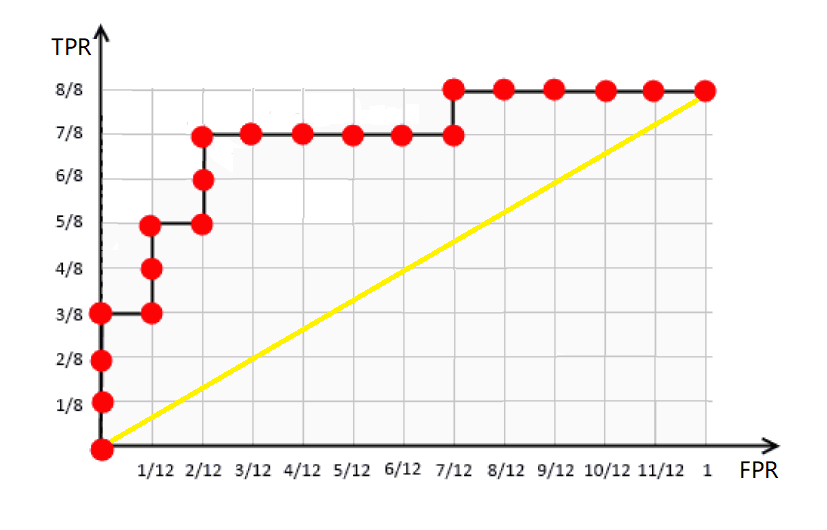
找最优阈值
在上面的ROC曲线中,黄色斜线叫基线,对应的是随机预测,阈值为0.5。因为二分类器最后输出的,是一个0到1之间的概率数字,我们想要根据这个概率判断用户好坏的话,就必须定义一个阈值:>=阈值预测为1,反之预测为0。而在众多阈值中,肯定存在一个最优阈值,使得模型性能最佳。与上面计算TPR思路一样,我们从两列数据出发,每一个阈值对应一列预测的y,对应一个混淆矩阵,就能计算出对应的ACC。
首先进行一个简单的推导:
| 缩写 | 含义 |
|---|---|
| P | 正例的个数 |
| N | 负例的个数 |
| A | 所有观察的个数,A=P+N |
| pos | 正例占总数的占比,pos=P/A |
| neg | 负例占总数的占比,neg=N/A |
则有:

在阈值确定后,正例和负例的比值就确定了,即斜率就确定了,改变ACC大小就能得到一系列斜率相同的平行直线,区别在于截距的大小不同。而ISO精度线和ROC曲线相切时,直线的截距取得最大,因为截距大小和ACC成正比,所以此时ACC取得最大,此时对应的预测概率就是最优阈值。引入反斜线TPR=1−FPR,与直线TPR=a∗FPR+b联立求解可得:TPR=ACC,即最大值ACC是ISO精度线与ROC曲线相切时,ISO精度线与反斜线交点对应的TPR。
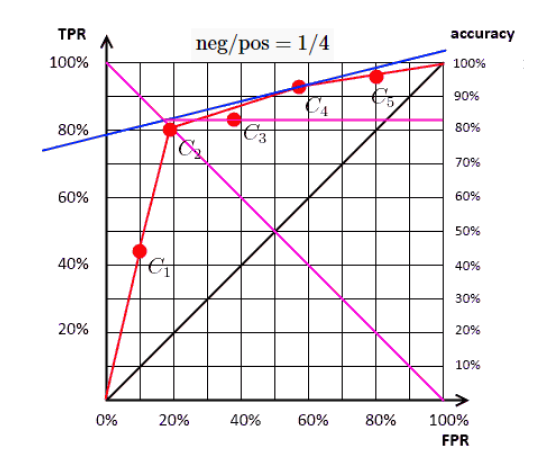
综上,ROC曲线找最优阈值的逻辑是:ISO精度线与ROC曲线相切时,ACC取得最大;ACC取得最大时,对应的就是最优阈值。所以如下图,前面计算ROC曲线时用的数据集,在第14个样例处ISO精度线与ROC曲线相切,取得的ACC最大值为17/20,最优阈值为0.72。
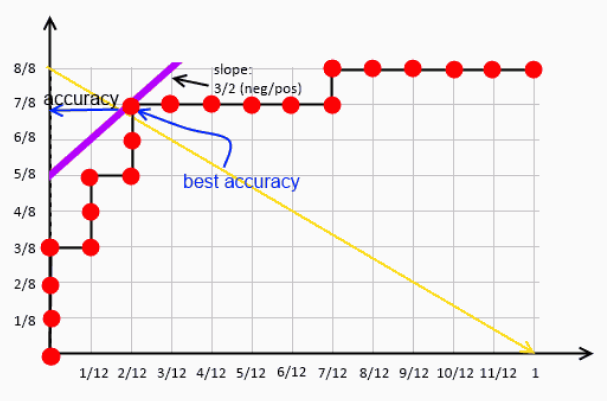
用ROC曲线评估模型
模型性能更佳,就意味着真实为1且预测为1的越多越好,真实为0且预测为1的越少越好,即TPR越大越好,且FPR越小越好。反应在图像上就是TPR越靠上、FPR越靠左。所以,用ROC曲线评估分类模型性能遵循下面准则:
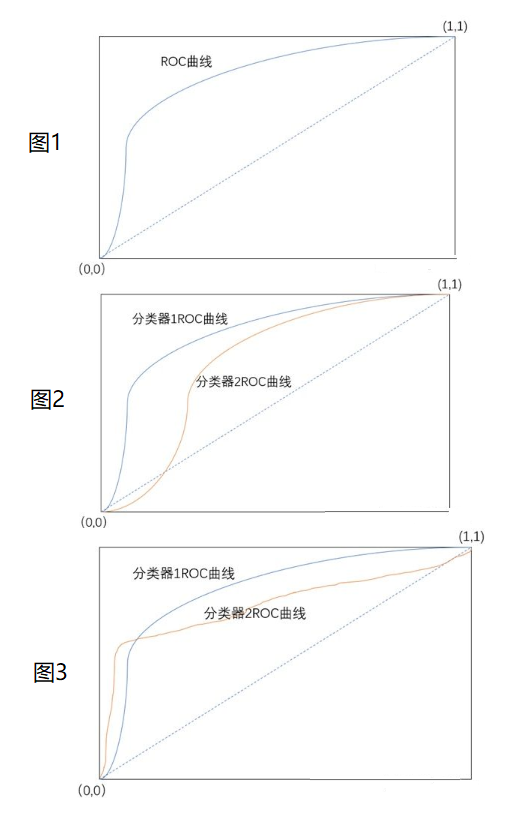
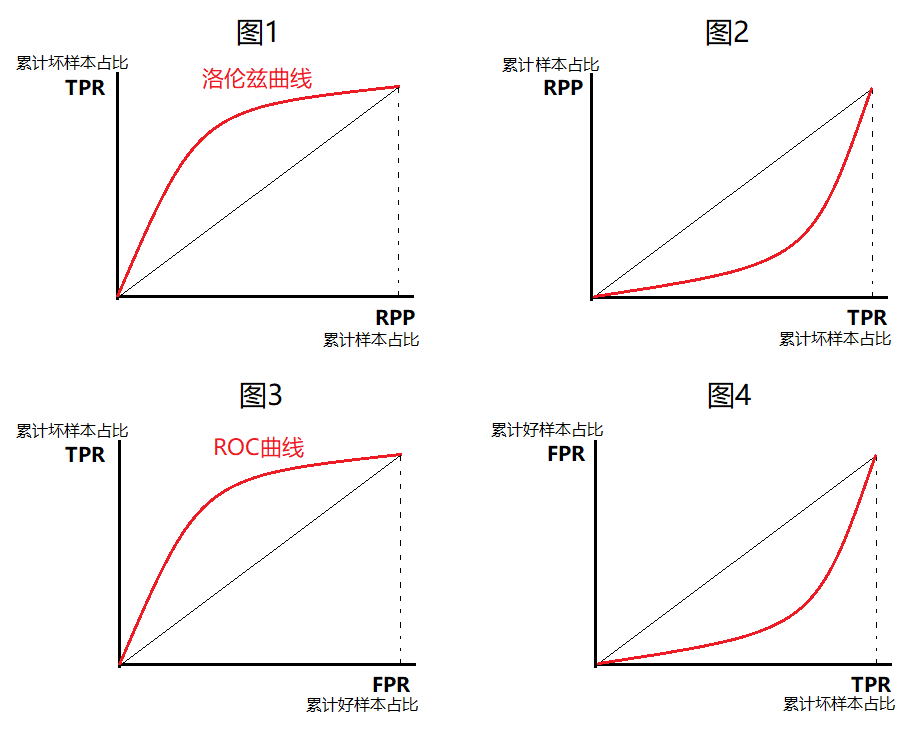
- 单个模型评估:曲线越靠近左上,模型分类性能更好,如图1
- 多个模型评估:要分两种情况讨论
- 情况1:在ROC曲线上,模型1完全包裹模型2,则模型1性能更好,如图2
- 情况2:在ROC曲线上,模型1不完全包裹模型2,则无法判断,需要借助AUC面积评估,如图3
1.2 AUC
如上所述,ROC曲线是一个定性的评估指标,并且很多时候并不能清晰的说明哪个分类器的效果更好,这时就需要引入一个可以量化的评估指标——AUC面积。ACU面积(Area Under Curve),又称ROC曲线下的面积,它描述的是分类器C随机抽取的一个正例的预测概率大于一个负例的预测概率的概率。简单地说,就是做随机抽样时,P(P) ≥ P(N)中 ≥ 成立的概率。
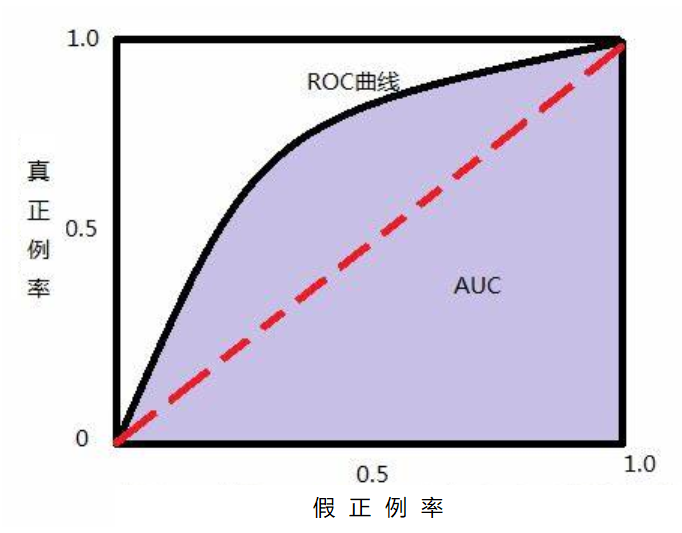
如上图紫色部分,ACU面积是指ROC曲线与下方坐标轴围成图形的面积,因为ROC曲线一般在斜线的上方,所以ACU面积的取值为[0.5,1],数值越大表示模型分类效果越好。同时,ACU面积和ROC曲线一样,不受正负样例分布的影响。其常用评估界值如下:
- 0.5 - 0.7:效果较低
- 0.7 - 0.85:效果一般
- 0.85 - 0.95:效果很好
- 0.95 - 1:效果非常好,但很可能过拟合,一般不太可能
1.3 K-S
K-S曲线的绘制
K-S曲线(Kolmogorov-Smirnov),绘图思路与ROC曲线类似,也是从真实y和预测概率(P(Y=1))两列数据出发,遍历每个阈值,计算出TPR、FPR、RPP等指标,最后完成绘图。不同的是,K-S曲线的绘图方法并不唯一,在横轴及纵轴的指标选取及使用上,可以有多种方式:
- 横轴:阈值 或 RPP,其中RPP=(TP+FP)/(P+N) ,表示预测为正例的比例,其实就是排序后的序号
- 纵轴:TPR与FPR作为纵轴
所以,K-S曲线实质上是由两条曲线构成,组合过程如下:
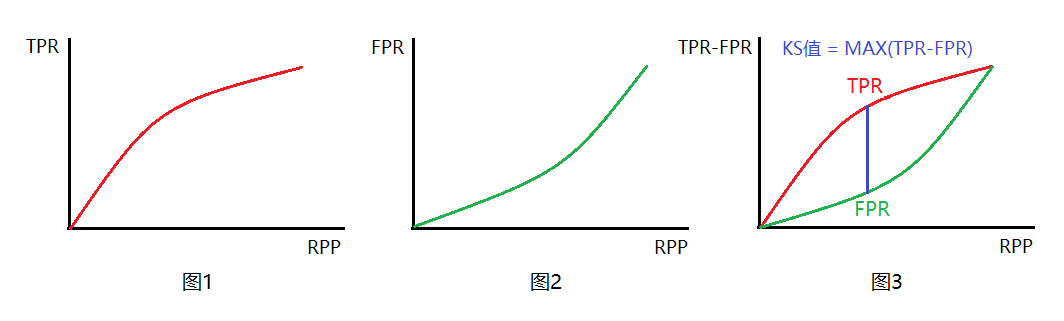
因为TPR与FPR是一对相互矛盾的指标,不可能同时取得最大或最小,所以中间一定存在一个临界值,使得TPR尽可能大的同时FPR尽可能的小,即两者差异最大。这个差异值反映在K-S曲线上就是两条曲线的间隔,众多差异值中最大的就叫做K-S值,K-S = MAX(TPR-FPR),它描述了模型对正负样例的区分能力,即模型对风险的区分能力。所以,对分类模型而言K-S值越大越好,KS值范围在[0,1],常见的评判标准如下:
- < 0.2:差
- 0.2-0.4:一般
- 0.41-0.5:不错
- 0.51-0.6:很好
- 0.61-0.75:非常好
- > 0.75:过高,模型很可能异常
需要特别说明的是,K-S曲线的画法并不唯一:有的资料横轴用阈值代替RPP,有的资料纵轴是用FPR-TPR,但都不影响最后结果,因为我们重点关注的是「TPR与FPR间的最大差异」 。
K-S值的计算
以评分卡为例,K-S的计算步骤如下:
-
计算每个评分区间的好坏账户数
-
计算每个评分区间的累计好账户数占总好账户数比率、累计坏账户数占总坏账户数比率
-
计算每个评分区间累计坏账户占比 与 累计好账户占比差的绝对值,然后对这些绝对值取最大值即得此评分卡的K-S值。
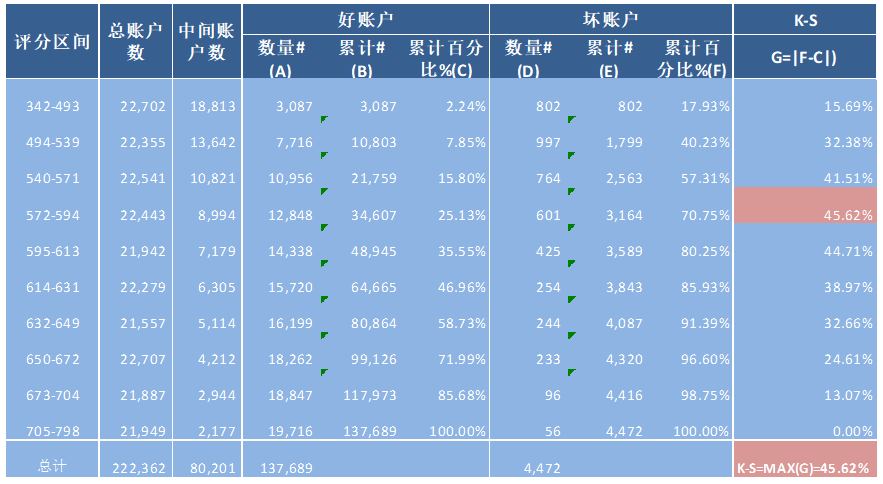
由上表可知,在风险评分 572 至 594 分的区间内好与坏累积分布之间的距离最大,评分为594分以下的所有账户中,累计坏账户占总坏账户比例为70.75%,累计好账户占总好账户的比例为25.13%。K-S指标为45.62%。
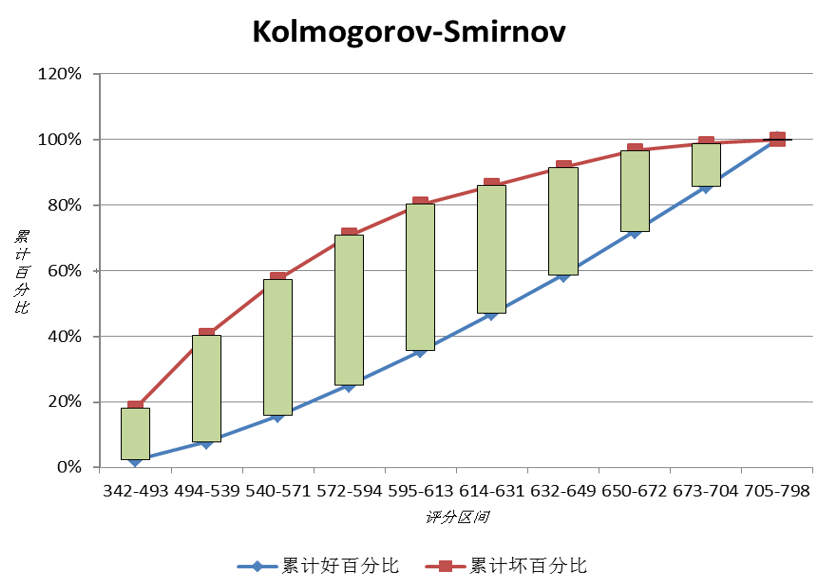
找最优阈值
由于K-S曲线能找出模型中差异最大的一个分段,因此可用于找最优阈值(cut_off),方法也很简单:取得K-S值时横轴对应的阈值就是最优阈值,若横轴是RPP,则最优阈值就是此RPP对应的阈值。
最后,可能大家会疑惑,已经有了AUC面积,为什么还要引入K-S指标呢?这就要明确两者的区别:
- AUC面积:在样本不均衡的情况下也能准确评估模型的好坏,看的是总体的分类效果
- K-S值:是通过找好坏客户累计分布的最大差异,评估模型对好坏客户的区分能力,看的是某个特定的分段
所以,一般情况下用AUC面积即可;如果业务更关注负样本,就会涉及到正负样例的区分度,用K-S值更好。但K-S值不能反映出所有分段的区分效果,评估时K-S值需要结合AUC面积、在哪个分段取得K-S值,三者结合才能更全面地评估模型。因为同样的K-S值,有的模型在高分段区分效果好,有的模型在低分段区分效果好,就会给模型应用带来差异,但通常而言,银行更关注的是坏客户(低分段客户)。
1.4 GINI
首先区分 基尼系数 与 基尼不纯度 两个概念,因为很多资料都把两者弄混了,而之后介绍的GINI是指基尼系数。
- 基尼系数:Gini Coefficient,最早用来衡量收入分配差异,后来也用作分类模型性能评估
- 基尼不纯度:Gini Impurity,也被称为基尼指数(Gini Index),用来构造决策树中的CART分类树
社会学中的GINI系数
20世纪初意大利经济学家基尼(Gini),根据洛伦兹曲线(即累计频数分布曲线)找出了判断分配平等程度的指标,它就是GINI系数,详见下图。
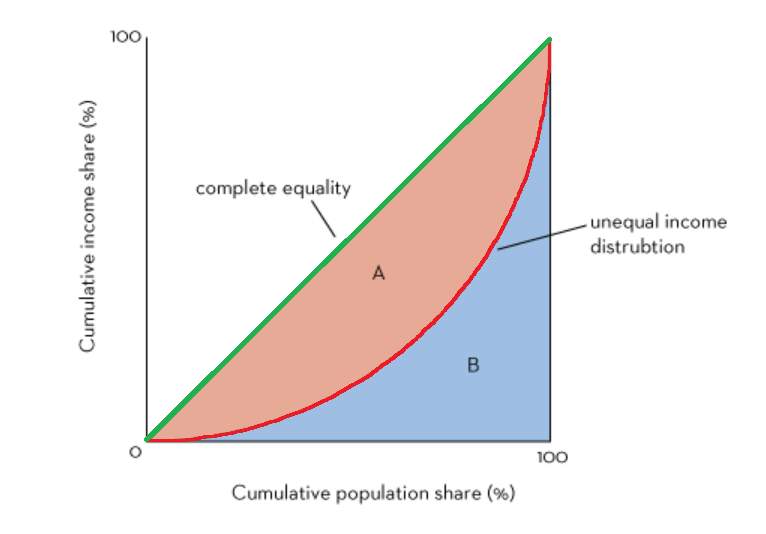
| 图形 | 含义 |
|---|---|
| 横轴 | 人口百分比累计(按收入从低到高进行人口累计) |
| 纵轴 | 收入百分比累计(指部分人口的收入占社会总收入比例) |
| 绿色斜线 | 收入分配绝对平等线 |
| 红色曲线 | 实际收入分配曲线(洛伦兹曲线,Lorenz Curve) |
| 基尼系数 | GINI = A / A+B,表示不平等程度,也称洛伦兹系数 |
由上图可知,若A=0,则GINI=0,表示收入和分配完全平等;若B=0,则GINI=1,表示收入和分配绝对不平等,因此GINI系数的取值是在[0,1]。
机器学习中的GINI系数
把上面的分析思路迁移到金融风控领域,就可以用GINI系数评估分类模型对好坏客户的区分能力,尤其是在评分卡模型的评估中(A卡:申请评分卡;B卡:行为评分卡)。与K-S曲线的绘制类似,GINI曲线图的画法也不唯一,但也不会影响计算和最后结果,总的来说分为两种情况:
-
样本中坏样本极少时:FP和FN很少,可以忽略不计,则RPP≈FPR,反映在图像上,就是图1变换到图3,此时洛伦兹曲线与ROC曲线近似重合,GINI系数的计算可以用GINI=2AUC - 1 或 GINI = A / A+B,推导如下。若把图3中的横轴坐标对调就得到图4,因此图3与图4都是正确的GINI系数曲线图。
RPP:Rate of positive predictions,所有预测中预测为正例的比例,反映在数据中就是序号,因为在构造洛伦兹曲线时,是先对样本安装风险评分升序过的 因为,FP和FN很少,可以忽略不计,则: RPP = (TP+FP)/(TP+FP+TN+FN) = FP/(FP+TN) = FPR GINI = A/(A + B) = (AUC - C)/(A + B) = (AUC -0.5)/0.5 = 2*AUC - 1 综上,GINI = 2AUC - 1 -
当坏样本较多,或好坏样本接近1:1时:用GINI系数的定义计算GINI: GINI = A / A+B。此时图1与图2都是正确的GINI系数曲线图(图2是由图1坐标轴对调而得)
GINI系数的计算
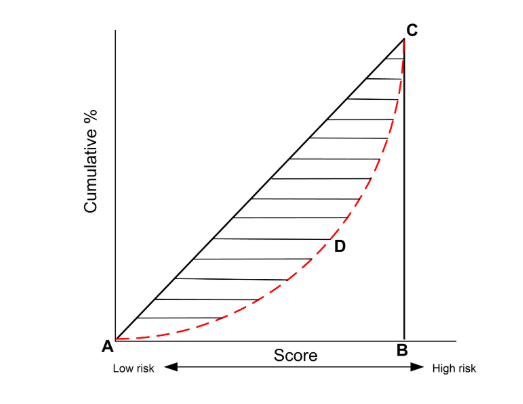
先基于评分对客户进行升序排列,然后以累计坏账户占比作为横轴,累计好账户占比作为纵轴,就能得到如下GINI曲线图,实质就是上面的图4。
然后,就可以对GINI系数进行计算,步骤如下:
-
计算每个评分区间的好坏账户数
-
计算每个评分区间的累计好账户数占总好账户数比率和累计坏账户数占总坏账户数比率
-
按照累计好账户占比和累计坏账户占比得出上图所示曲线ADC
-
计算出图中阴影部分面积,阴影面积占直角三角形ABC面积的百分比,即为GINI系数
具体计算如下表:
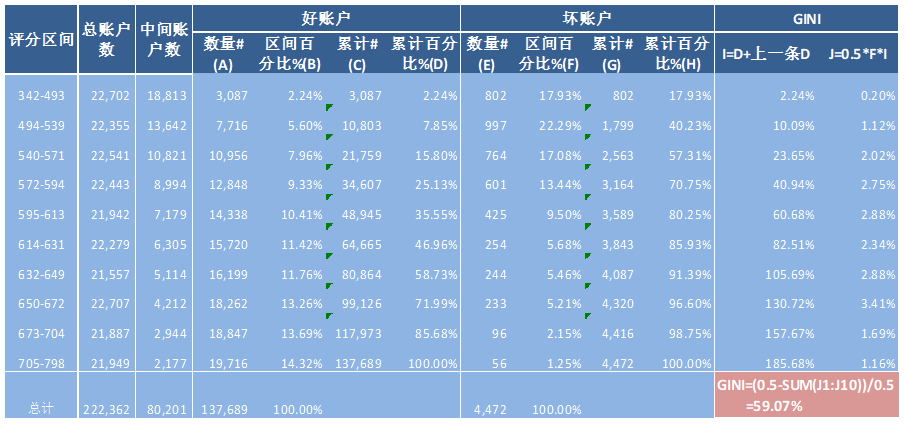
需要特别指出的是,GINI系数定义中的公式:GINI = A / A+B,虽然是一个极为简明的数学表达式,但它并不具有实际的可操作性,因此在计算GINI系数时都是采用近似估算的思路,这就衍生出好几种方法来计算GINI系数。如下面的公式,其中cp表示累计,X、Y分别表示好客户、坏客户,所以上图中数据GINI = 1-SUM(I*F)=59.07%
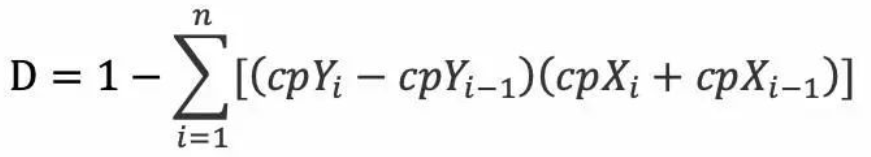
GINI系数的评估标准
根据一般经验,GINI系数评判标准如下:
- 申请评分卡
- < 30% : 差
- 30%-40% : 一般
- 41%-50% : 好
- 51%-60% : 非常好
- > 60% : 越高越有过拟的可能
- 行为评分卡
- Gini可能会超过80%
- Gini<60%,可能模型有问题
虽然Gini指标与K-S一样也是金融评分模型界通用的核心指标,但是它的使用也是有一些需要注意的地方:
-
评估评分卡的区分能力时,如果坏客户的定义不是那么严格,Gini系数对应代表的区分能力可能被夸大效果
-
Gini对目标变量类别的定义比较敏感,比如账户的好坏
所以要想Gini指标精确有效,那么目标变量Y的定义在评分卡开发初期是十分重要和严谨的步骤。
1.5 小结
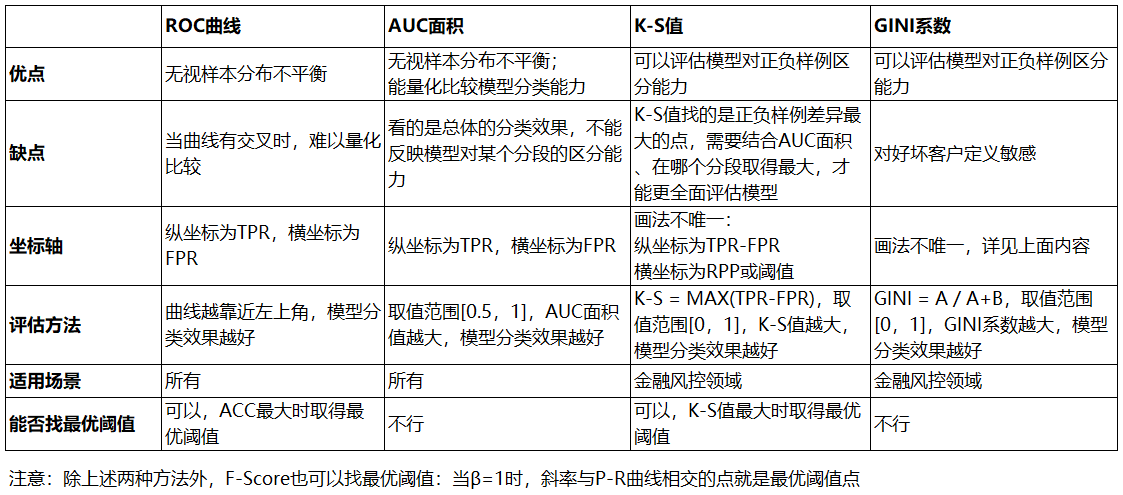
最后,对上述介绍的混淆矩阵衍生评估指标,做一个简单的总结: