TensorFlow线性回归操作
02.TensorFlow 线性回归
实验目的
1.掌握使用TensorFlow进行线性回归
2.掌握TensorFlow的基本运行流程
实验原理
线性回归是用来度量变量间关系的统计技术。该算法的实现并不复杂,但可以适用于很多情形。正是因为这些原因,以线性回归作为开始学习TensorFlow的开始。
不管在两个变量(简单回归)或多个变量(多元回归)情形下,线性回归都是对一个依赖变量,多个独立变量xi,一个随机值b间的关系建模。利用TensorFlow实现一个简单的线性回归模型:分析一些代码基础及说明如何在学习过程中调用各种重要组件,比如cost function或梯度下降算法。
实验环境
Python 3.6.0
Pycharm
实验内容
使用TensorFlow进行线性回归操作。
实验步骤
1.打开Pycharm,右键选择New=>Python File,创建名为linear_regression的Python文件。编写tensorflow线性回归代码。
导入实验所需要的模块
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
4.设置训练参数,learning_rate=0.01,training_epochs=1000,display_step=50。
learning_rate=0.01
training_epochs=1000
display_step=50
5.创建训练数据
train_X=np.asarray([3.3,4.4,5.5,6.71,6.93,4.168,9.779,6.182,7.59,2.167,7.042,10.791,5.313,7.997,5.654,9.27,3.1])
train_Y=np.asarray([1.7,2.76,2.09,3.19,1.694,1.573,3.366,2.596,2.53,1.221,2.827,3.465,1.65,2.904,2.42,2.94,1.3])
n_samples=train_X.shape[0]
6.构造计算图,使用变量Variable构造变量X,Y,代码如下:
X=tf.placeholder("float")
Y=tf.placeholder("float")
7.设置模型的初始权重
W=tf.Variable(np.random.randn(),name="weight")
b=tf.Variable(np.random.randn(),name='bias')
8.构造线性回归模型
pred=tf.add(tf.multiply(X,W),b)
9.求损失函数,即均方差
cost=tf.reduce_sum(tf.pow(pred-Y,2))/(2*n_samples)
10.使用梯度下降法求最小值,即最优解
optimizer=tf.train.GradientDescentOptimizer(learning_rate).minimize(cost)
11.初始化全部变量
init = tf.global_variables_initializer()
12.使用tf.Session()创建Session会话对象,会话封装了Tensorflow运行时的状态和控制。
with tf.Session() as sess:
sess.run(init)
13.调用会话对象sess的run方法,运行计算图,即开始训练模型。
#调用会话对象sess的run方法,运行计算图,即开始训练模型
for epoch in range(training_epochs):
for (x,y) in zip(train_X,train_Y):
sess.run(optimizer, feed_dict={X: x, Y: y})
if(epoch + 1) % display_step == 0:
c = sess.run(cost,feed_dict={X:train_X,Y:train_Y})
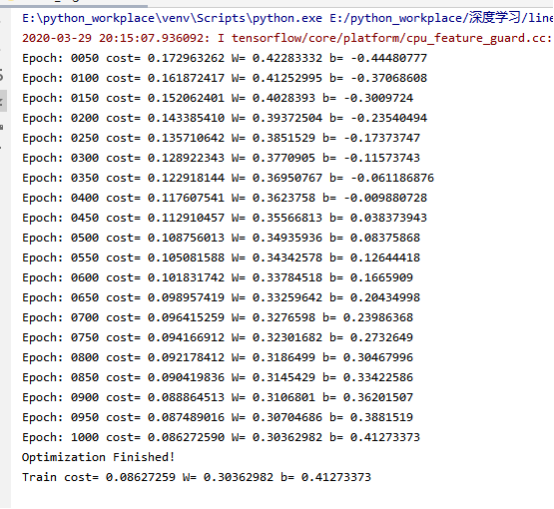
print("Epoch:",'%04d' % (epoch+1),"cost=","{:.9f}".format(c),"W=",sess.run(W),"b=",sess.run(b))
print("Optimization Finished!")
14.打印训练模型的代价函数。
training_cost = sess.run(cost, feed_dict={X: train_X, Y: train_Y})
print("Train cost=", training_cost, "W=", sess.run(W), "b=", sess.run(b))
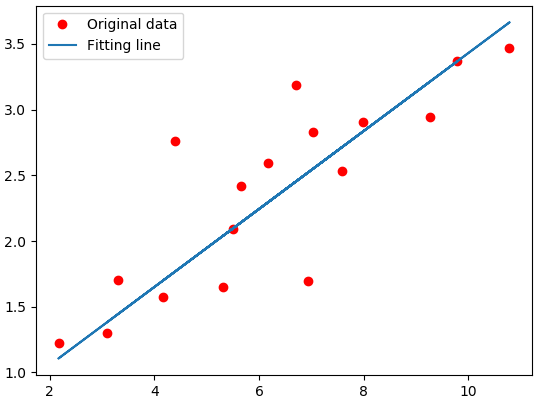
15.可视化,展现线性模型的最终结果。
plt.plot(train_X, train_Y, 'ro', label='Original data')
plt.plot(train_X, sess.run(W) * train_X + sess.run(b), label="Fitting line")
plt.legend()
plt.show()
16.完整代码如下:
import tensorflow as tf import numpy as np import matplotlib.pyplot as plt #设置训练参数, learning_rate=0.01 training_epochs=1000 display_step=50 #创建训练数据 train_X=np.asarray([3.3,4.4,5.5,6.71,6.93,4.168,9.779,6.182,7.59,2.167,7.042,10.791,5.313,7.997,5.654,9.27,3.1]) train_Y=np.asarray([1.7,2.76,2.09,3.19,1.694,1.573,3.366,2.596,2.53,1.221,2.827,3.465,1.65,2.904,2.42,2.94,1.3]) n_samples=train_X.shape[0] X=tf.placeholder("float") Y=tf.placeholder("float") #设置模型的初始权重 W=tf.Variable(np.random.randn(),name="weight") b=tf.Variable(np.random.randn(),name='bias') #构造线性回归模型 pred=tf.add(tf.multiply(X,W),b) #求损失函数,即均方差 cost=tf.reduce_sum(tf.pow(pred-Y,2))/(2*n_samples) #使用梯度下降法求最小值,即最优解 optimizer=tf.train.GradientDescentOptimizer(learning_rate).minimize(cost) #初始化全部变量 init = tf.global_variables_initializer() #使用tf.Session()创建Session会话对象,会话封装了Tensorflow运行时的状态和控制。 with tf.Session() as sess: sess.run(init) #调用会话对象sess的run方法,运行计算图,即开始训练模型 for epoch in range(training_epochs): for (x,y) in zip(train_X,train_Y): sess.run(optimizer, feed_dict={X: x, Y: y}) if(epoch + 1) % display_step == 0: c = sess.run(cost,feed_dict={X:train_X,Y:train_Y}) print("Epoch:",'%04d' % (epoch+1),"cost=","{:.9f}".format(c),"W=",sess.run(W),"b=",sess.run(b)) print("Optimization Finished!") #打印训练模型的代价函数 training_cost = sess.run(cost, feed_dict={X: train_X, Y: train_Y}) print("Train cost=", training_cost, "W=", sess.run(W), "b=", sess.run(b)) #可视化,展现线性模型的最终结果 plt.plot(train_X, train_Y, 'ro', label='Original data') plt.plot(train_X, sess.run(W) * train_X + sess.run(b), label="Fitting line") plt.legend() plt.show()
18.运行结果为: