《程序员的数学课》模块二 代数与统计

05 | 求极值：如何找到复杂业务的最优解？

• 求导法
• 梯度下降法

最优解的思考方法：想要找到一个复杂业务的最优解，就先需要找到影响这个事情的关键因素，以及关键因素之间的关系，而这个过程就是形式化定义的过程，把问题形式化定义后，再去追逐收益的最大化。

形式化定义：用函数去表达需要用文字描述的问题。动作、收益、风险，用函数建立起联系

求导法

导数基础知识点-传送门

14个基本初等函数的导数

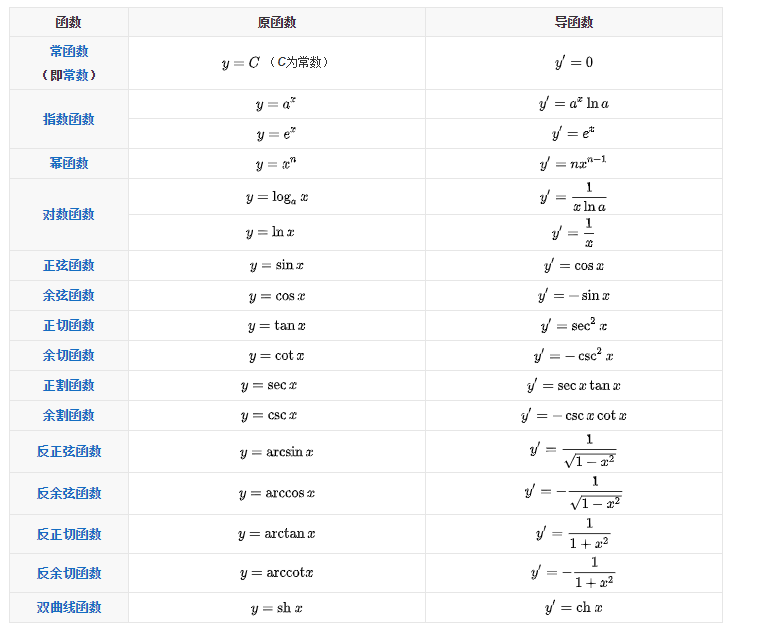
导数的四则运算

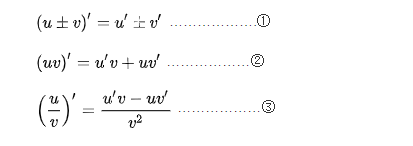
梯度下降法

• 利用导数的含义斜率，斜率为整数则是上升趋势，斜率为负数则是下降趋势
• 围绕这个性质，就可以通过多轮迭代，逐步去逼近函数的极值点

用数学语言描述：

• 定义一下函数的梯度，对于函数 f(x,y)，常用 ▽f(x,y) 来表示函数的梯度。其中 x、y 表示函数有两个或多个自变量，是个多元函数。
• 梯度本身是个向量，表示的是函数在自变量构成的空间中，变化率最快的方向，其计算式为：

[我觉得]变化率最快的方向：斜率从上升趋势突然变为下降趋势，这个突然变化的点，就是变化率最快的方向

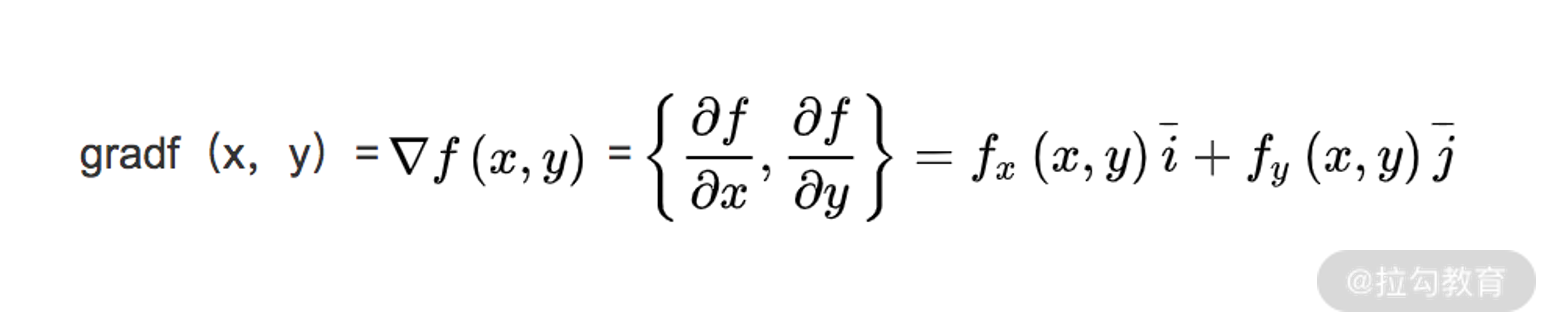
对梯度下降法的原理进行分析：

第 1 步，是把一些要用的公式预先推导出来。
第 2 步，计算当前点的梯度，找到当前点变化率最快的方向。
第 3 步，(xtemp,ytemp) = (xtemp,ytemp) - a×▽f(xtemp，ytemp) 表达的含义是，从当前的点，朝着这个变化率最快方向的反方向，移动一小步后，来更新当前点，这里有两个要点：

• 之所以是“反方向”，是因为我们要求解的是函数的极小值；如果是极大值，就不是反方向了，公式中的“负号”就要修改为“正号”。
• “移动一小步”的实现，一般用学习率 a 来控制。通常 a 不会很大，比如设置为 0.1、0.05 等等。如果 a 过大，则可能会出现移动后“跳过”极值的可能；如果 a 过小，无非就是迭代次数多一些而已。这一步是梯度下降法最关键的步骤。
  第 4 步，就是当迭代到极值附近时，就终止条件的判断了。

案例：用户营销红包的投放

Q1：对于一件商品，投放多少金额的红包，能让你的利润最大？
A1：

• 分析：投放给用户的红包金额越高，用户购买这件商品的可能性越大。然而投放红包的金额越高，利润空间也越小。
• 形式化定义：假设，用户购买商品的概率与投放的补贴金额的关系为 p(x)。因此，投放金额为 x 的红包额后，商品的利润r(x)可以定义为

r(x) = p(x)*(m-x-c)
注：m为商品的价格，c为商品的成本价

• 有了形式化定义之后，才可以进行业务策略的优化，也就是追逐收益最大化。
• “追逐收益最大化”就是求解这个函数的最值 max(r(x))
• 令目标函数的一阶导数为零，并求解方程的解，这种方法称作求导法。

方法总结：
第1步，分析关键因素、因素之间的关系
第2步，对其因素进行形式化定义，获得函数
第3步，对函数求导，获取最值

Q2：公司 BI 同事经过深度分析业务数据得到，商品的购买概率和补贴额的关系为 p(x) = 2÷(1+e-x) - 1。
A2：

1. 获取形式化函数：r(x) = p(x)*(m - x - c) = (2÷(1+e-x) - 1)×(16 - x - 8)
2. 用求导法获取最值：如下截图，再使用求导法的话，就很难解了，就要用梯度下降法求解
   
3. 用梯度下降法获取最值：

• 第一步，写出目标函数 r(x) 的梯度函数：
  
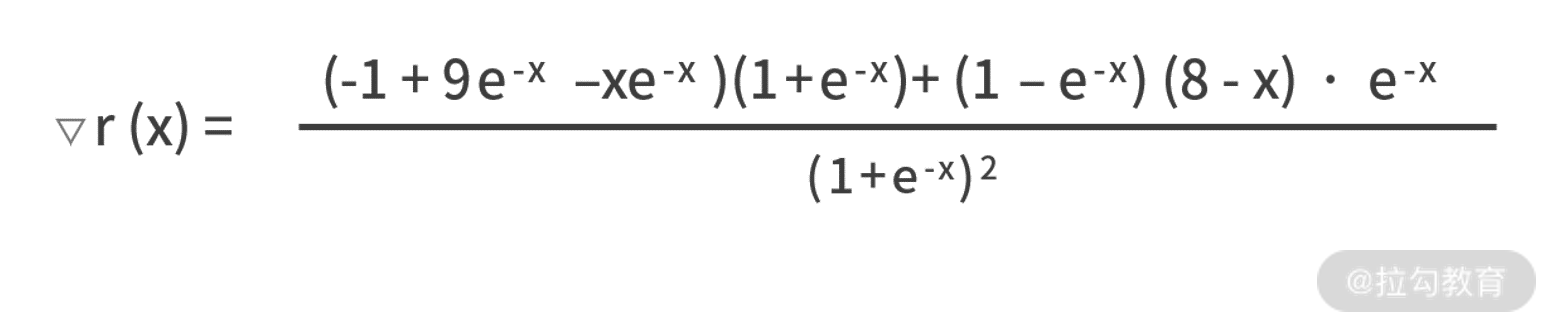
• 第二步，设置学习率a=0.01，最大迭代次数1000，然后就需要利用 xtemp = xtemp - a×▽r(xtemp) 来逐轮迭代。
  代码如下：

import math
def grad(x):
    fenzi1 = (-1 + 9 * math.exp(-x) - x * math.exp(-x)) * (1 + math.exp(-x))
    fenzi2 = -(8 - x) * (1 - math.exp(-x)) * math.exp(-x)
    fenmu = math.pow(1 + math.exp(-x), 2)
    return (fenzi1 - fenzi2) / fenmu
def main():
    a = 0.01
    maxloop = 1000
    xtemp = 0.1
    for _ in range(maxloop):
        g = grad(xtemp)
        if g < 0.00005:
            break
        xtemp = xtemp + a * g
    print(xtemp)
if __name__ == '__main__':
    main()

梯度下降法和求导法异同点：

相对求导法，梯度下降法显然是更厉害的算法。不过，它也有一些局限性：

• 它需要配置一些算法参数，如学习率、停止条件等。如果配置不好，可能会导致算法失效。例如，在本课时的例子中，如果学习率不小心设置为 0.7 以上，结果就不再是 2.42 了。这是因为学习率过高，导致了每一次迭代自变量“移动的步伐太大”，而频繁跨越最值无法收敛。

总结

相比求导法而言，梯度下降法的适用性更广、计算更简单，但计算量相对更多。就梯度下降法本身而言，它的局限性是依赖学习率、终止条件、初始值等参数的配置，并且只适用于凸函数。