第一章 模式识别基本概念 笔记

什么是模式识别

模式识别：根据已有知识的表达，针对待识别模式，判别其决策所属的类别或者预测其对应的回归值。
分类：输出量是离散的类型表达，即输出待识别模式所属的类别。
回归：输出量是单个/多个维度的连续信号表达（回归值）。
回归是分类的基础：离散的类别值是由回归值做判别决策得到的。

模式识别数学表达

数学解释：模式识别可以看作一种函数映射f(x)，将待识别模式 x 从输入空间映射到输出空间。
输入空间：原始输入数据 x 所在的空间，空间维度：输入数据的维度
输出空间：输出的类别/回归值y所在的空间，空间维度：1维、类别的个数、回归值维度
特征向量：

特征向量的相关性

欧式距离：

机器学习基本概念

模型的参数和结构：

线性模型：

非线性模型：

样本量 vs 模型参数量

• 训练样本个数 = 模型参数个数 ：参数有唯一解
• 训练样本个数 > 模型参数个数 ：没有准确的解
• 训练样本个数 < 模型参数个数 ：无数个解/无解

目标函数：以待学习的模型参数作为自变量，以训练样本作为给定量的函数。

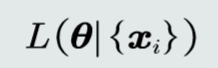
优化算法：

机器学习流程示意图：

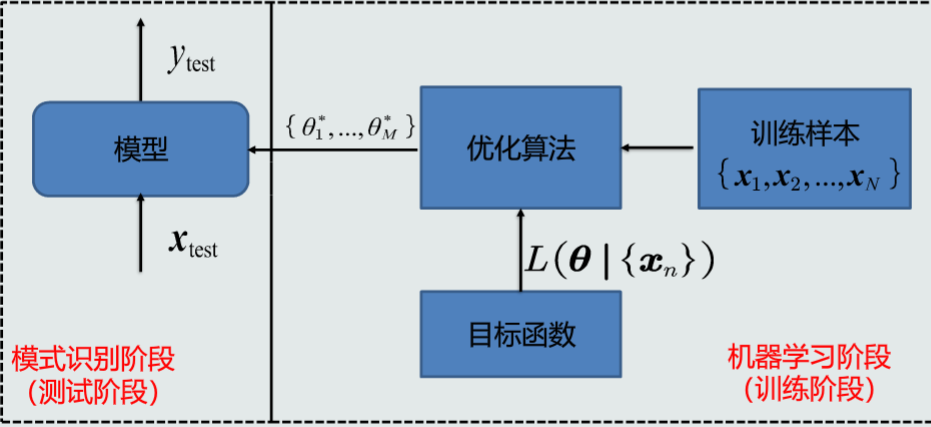
监督式学习：

无监督式学习：

模型的泛化能力

训练集：模型训练所用的样本数据。
测试集：测试模型性能所用的样本数据。
误差：模型给出的预测/决策输出与真值之间的差异。
训练误差：模型在训练集上的误差。
测试误差：模型在测试集上的误差。它反映了模型的泛化能力，也称作泛化误差。
过拟合：模型训练阶段表现很好，但是在测试阶段表现很差。

评估方法和性能指标

留出法：

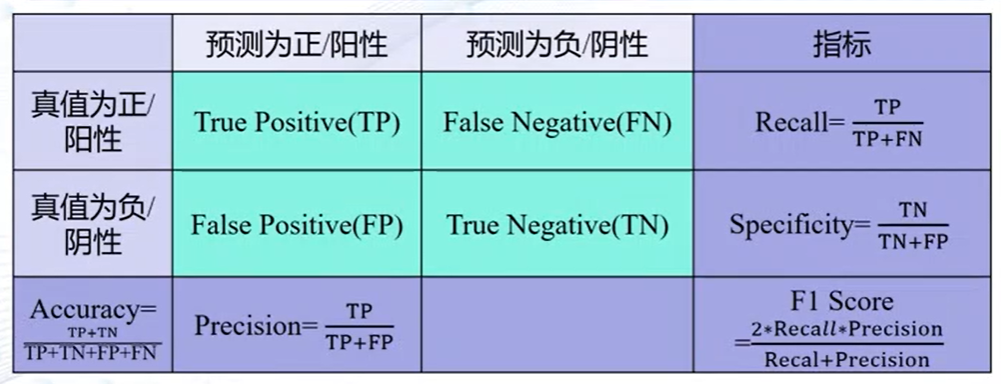
二分类问题性能指标：