莫比乌斯反演

引入：

设 \(g(i)\) 为\(i\)的约数和，
求\(f(n)=\sum\limits_{d|n} g(d)\).

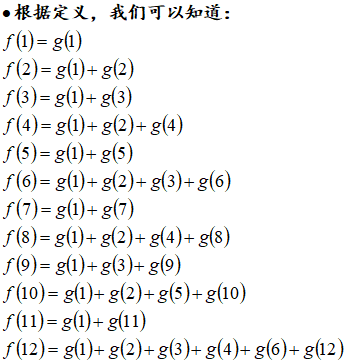
那么观察上面的等式，可以用\(f(n)\)表示\(g(n)\)：

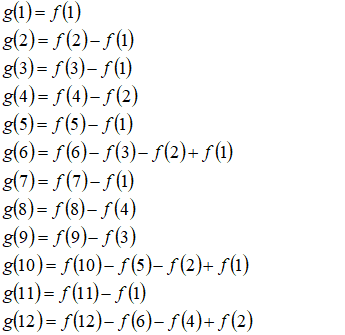
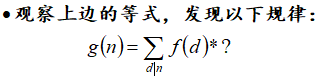
进入正题：

莫比乌斯反演的公式

\[f(n)=\sum\limits_{d|n}g(d)\Rightarrow g(n)=\sum\limits_{d|n}f(\frac{n}{d})×\mu(d) \]

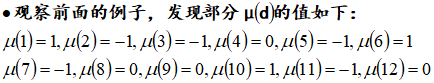
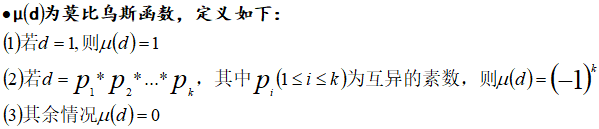
莫比乌斯函数的性质

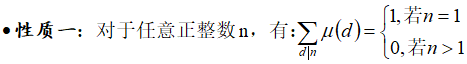
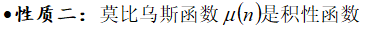
计算莫比乌斯函数

可以用线性筛法\(O(n)\)完成，参考如下代码：

inline void xxs()
{
	μ[1]=1;
	for(rll i=2;i<maxn;i++)
	{
		if(!fl[i])
		{
			prime[++cnt]=i;
			μ[i]=-1;
		}
		for(rll j=1;j<=cnt&&i*prime[j]<maxn;j++)
		{
			fl[i*prime[j]]=1;
			if(!(i%prime[j])) break;
			μ[i*prime[j]]=-μ[i];
		}
	}
}

莫比乌斯反演的性质

莫比乌斯反演的变形

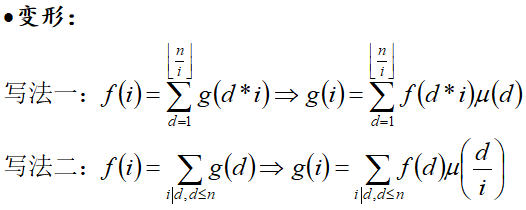
莫比乌斯反演的应用

例题

YY的GCD

题目描述
YY虐完数论后给傻×kAc出了一题.
给定N, M,求1<=x<=N, 1<=y<=M且gcd(x, y)为质数的(x, y)有多少对k.
Ac这种傻×必然不会了，于是向你来请教……
输入格式
第一行一个整数T 表述数据组数.
接下来T行，每行两个正整数，表示N, M.
输出格式
T行，每行一个整数表示第i组数据的结果.
样例
样例输入

2
10 10
100 100

样例输出

30
2791

数据范围与提示
\(T = 10000\)， \(N, M \leq 10000000\)

具体推式子过程就不再赘述了.
(主要因为我懒，不愿意打公式)

这里介绍一个结果计算从\(O(n)\)变成\(O(\sqrt{n})\)的小技巧：整除分块.
对于每一个\(\lfloor\frac{n}{i}\rfloor\)，我们可以通过打表(或理性的证明)可以发现：有许多\((\lfloor\frac{n}{i}\rfloor)\)的值是一样的，而且它们呈一个块状分布；再通过打表之类的各种方法,我们惊喜的发现对于每一个值相同的块，它的最后一个数就是\(\frac{n}{\frac{n}{i}}\).得出这个结论后，我们就可以做的\(O(\sqrt{n})\)处理了.

if(n>m) swap(n,m);
for(rll i=1,j;i<=n;i=j+1)
{
	j=min(n/(n/i),m/(m/i));
	ans+=(n/i)*(m/i)*(sum[j]-sum[i-1]);
}

参考代码

#include<bits/stdc++.h>
#define ll long long
#define rg register
#define maxn 10000001
#define rll rg ll
using namespace std;
bool fl[maxn];
ll prime[maxn],miu[maxn],cnt;
ll sum[maxn];
ll tmp[maxn];
ll t,n,m,ans;
inline void xxs()
{
	miu[1]=1;
	for(rll i=2;i<maxn;i++)
	{
		if(!fl[i])
		{
			prime[++cnt]=i;
			miu[i]=-1;
		}
		for(rll j=1;j<=cnt&&i*prime[j]<maxn;j++)
		{
			fl[i*prime[j]]=1;
			if(!(i%prime[j])) break;
			miu[i*prime[j]]=-miu[i];
		}
	}
	for(rll i=1;i<=cnt;i++)
		for(rll j=1;prime[i]*j<maxn;j++)
			tmp[prime[i]*j]+=miu[j];
	for(rll i=1;i<maxn;i++)
		sum[i]=sum[i-1]+tmp[i];
}
int main()
{
	ios::sync_with_stdio(0);
	xxs();
	cin>>t;
	while(t--)
	{
		ans=0;
		cin>>n>>m;
		if(n>m) swap(n,m);
		for(rll i=1,j;i<=n;i=j+1)
		{
			j=min(n/(n/i),m/(m/i));
			ans+=(n/i)*(m/i)*(sum[j]-sum[i-1]);
		}
		cout<<ans<<endl;
	}
	return 0;
}