DS博客作业02--栈和队列
0.PTA得分截图

1.本周学习总结(0-4分)
1.1 总结栈和队列内容
顺序栈
· 结构体定义:
typedef struct
{
int data[MAXSIZE];
int top;//栈顶元素位置
}SqStack,*Stack;
· 注意事项:栈只能在栈顶进行出栈(pop)和入栈(push)操作,并且是先进先出的。
· 顺序栈的图示:

· 顺序栈的三种状态:
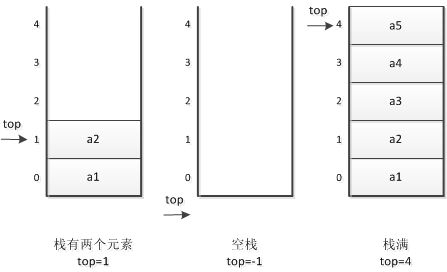
· 初始状态时,栈顶指针的值为-1(因为栈空条件),当top=MAXSIZE-1时栈满,进栈top+1,出栈top-1。
· 顺序栈的几种操作:
(1)初始化栈:
void InitStack(Stack &S)
{
S=(SqStack*)malloc(sizeof(SqStack));
S->top=-1;
}
(2)进栈:
bool PushStack(Stack &S,int e)
{
if(s->top==MAXSIZE)return false;//当栈达到最大容量
S->top++;
S->data[S->top]=e;
return true;
}
(3)出栈:
bool PopStack(Stack &S,int e)
{
if(s->top==-1)return false;//当栈空时,栈下溢
e=S->data[S->top];
S->top--;
return true;
}
(4)销毁栈:
void DestroyStack(SqStack &s)
{
delete s;
}
链栈:
· 结构体定义:
typedef struct linknode
{ ElemType data; //数据域
struct linknode *next; //指针域
} LiNode,*LiStack;
· 链栈图示(带头节点):

· 链栈的四要素:
栈空条件:S->next==NULL;
进栈操作:使用头插法,将节点插到头结点后。
出栈操作:取出头结点后的第一个节点,并释放内存。
栈空条件:由于链栈采用链结构,故不用考虑栈满。
· 链栈的几种操作:
(1)链栈的初始化:
void InitStack(LiStack &s)
{ s=new LiNode;
s->next=NULL;
}
对应的C++模板操作:stack<类型> 名称;例如:stack
(2)进栈:
void Push(LiStack &s,ElemType e)
{ LiStack p;
p=new LiNode;
p->data=e; //新建元素e对应的节点*p
p->next=s->next; //插入*p节点作为开始节点
s->next=p;
}
对应的C++模板操作:s.push(e);//入栈元素e。
图示:

(3)出栈:
bool Pop(LiStack &s,ElemType &e)
{ LiStack p;
if (s->next==NULL)//栈空的情况
return false;
p=s->next;//p指向开始节点
e=p->data;
s->next=p->next;//删除*p节点
free(p);//释放*p节点
return true;
}
对应的C++模板操作:S.pop();这里要和S.top区分一下,前者做的是物理删除,并不返回栈顶元素的值,后者返回栈顶元素的值。
图示:
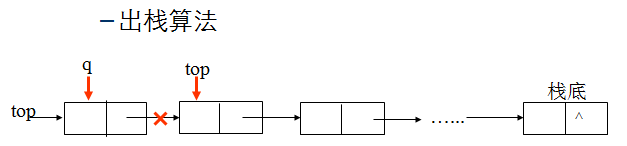
(4)取栈顶元素:
bool GetTop(LiStack s,ElemType &e)
{ if (s->next==NULL) //栈空的情况
return false;
e=s->next->data;
return true;
}
对应的C++模板操作:3.s.top();//返回栈顶元素
(5)判断栈是否为空:
bool StackEmpty(LiStack s)
{
return(s->next==NULL);
}
对应的C++模板操作:s.empty();//当栈空时,返回true。
(6)销毁栈:
void DestroyStack(LiStack &s)
{ LiStack p;
while (s!=NULL)
{ p=s;
s=s->next;
free(p);
}
}
栈的应用
1.栈和递归:
递归过程退回的顺序是它前行顺序的逆序。显然这符合栈的存储方式。简单的说,就是在前行阶段,对于每一层递归,函数的局部变量、参数值以及返回地址都被压如栈中。在退回阶段,位于栈顶的局部变量、参数值和返回地址被弹出,用于返回调用层次中执行代码的其余部分,也就是恢复了调用的状态。
2.进制转换
在计算机中存储的数据都是二进制,所以往往需要把十进制数据转换成二进制,转换的过程实际就是除2取余数,这其中我们可以看到最先求得余数实际是个位数,书写一个数据的时候都是先书写高位的数据,而后依次到个位。这正好和栈后进先出的特性吻合,因此可以使用栈来存储。
3.表达式求值(中缀转后缀)
首先置操作数数组postexp为空,表达式的起始符'='为运算符栈OP的栈底元素;if(是数字)postexp[]=OP.top(),OP.pop();if(是运算符) 与OPTR栈顶元素进行比较,按优先级进行操作;
(1)if栈顶元素<输入算符,则算符压入OP栈,并接收下一字符
(2)if栈顶元素=运算符但≠‘=’,则脱括号(弹出左括号)并收下一字;
(3)if栈顶元素>运算符,则退栈、按栈顶计算,将结果压入OP栈。
(4)且该未入栈的运算符要保留,继续与下一个栈顶元素比较!
另附上map容器详解网址:https://blog.csdn.net/Dawn_sf/article/details/78456747
4.迷宫
迷宫中走不通的路要原路返回,很适合栈
其中栈的数据结构为:
typedef struct
{ Box data[MaxSize];
int top;//栈顶指针
} StType;//顺序栈类型
方块的数据结构为:
typedef struct
{ int i;//当前方块的行号
int j;//当前方块的列号
int nd;//nd是下一可走相邻的方位号
} Box;//定义方块类型
1.2队列的存储结构及操作
顺序队:
结构体定义:
typedef struct
{ ElemType data[MaxSize];
int front,rear; //队首和队尾指针
} SqQueue;
图示(附几种操作):

注意事项:1.rear总是指向队尾元素。 2.元素进队,rear增1。 3.front指向当前队中队头元素的前一位置。 4.元素出队,front增1
四要素:
· 队空条件:front = rear
· 队满条件:rear = MaxSize-1
· 元素e进队:rear++; data[rear]=e;
· 元素e出队:front++; e=data[front];
···
顺序队的几种操作:
(1)初始化队列:
void InitQueue(SqQueue *&q)
{ q=(SqQueue *)malloc (sizeof(SqQueue));
q->front=q->rear=-1;
}
注意此时rear和front都为-1。
(2)进队列:
bool enQueue(SqQueue *&q,ElemType e)
{ if (q->rear==MaxSize-1)//队满上溢出
return false;
q->rear++;
q->data[q->rear]=e;
return true;
}
注意:1.首先要判断队列是不是满的。 2.先将队尾指针rear自增,再将元素添加到该位置。
(3)出队列:
bool deQueue(SqQueue *&q,ElemType &e)
{ if (q->front==q->rear)//队空下溢出
return false;
q->front++;
e=q->data[q->front];
return true;
}
注意:1.首先要判断队列是否是空的。 2.队首指针自增,然后将front位置的值给e。
链队列
链队列的结构体定义:
typedef struct qnode
{ ElemType data; //数据元素
struct qnode *next;
} DataNode;
typedef struct
{ DataNode *front; //指向单链表队头结点
DataNode *rear; //指向单链表队尾结点
} LinkQuNode,*LinkList;
图解:
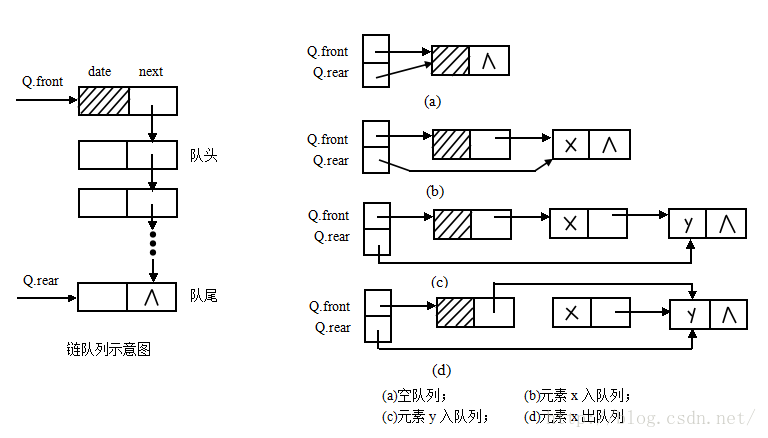
(1)初始化队列InitQueue(q)
void InitQueue(LinkQuNode *&q)
{ q=new LinkQuNode;
q->front=q->rear=NULL;
}
对应的C++模板操作为:queue<类型>队列名称;如:queue
(2)判断队列是否为空QueueEmpty(q)
若队列q满足q->front==q->rear条件,则返回true;否则返回false。
bool QueueEmpty(SqQueue q)
{
return(q->front==q->rear);
}
对应的C++模板操作为:Q.empty();//队空时返回true。
(3)进队列:
void enQueue(LinkQuNode *&q,ElemType e)
{ DataNode *p;
p=(DataNode *)malloc(sizeof(DataNode));
p->data=e;
p->next=NULL;
if (q->rear==NULL)
q->front=q->rear=p;
else
{ q->rear->next=p;
q->rear=p;
}
}
对应的C++模板操作为:Q.push(e);
注意:链队不需要考虑队满的情况。
(4)出队列:
bool deQueue(LinkQuNode *&q,ElemType &e)
{ DataNode *t;
if (q->rear==NULL) return false; //队列为空
t=q->front;
if (q->front==q->rear)
q->front=q->rear=NULL;
else
q->front=q->front->next;
e=t->data;
free(t);
return true;
}
对应的C++模板操作为:Q.pop();//弹出队列的第一个元素,但并不会返回被弹出元素的值。
注意:无论是顺序队还是链队在出队时都要考虑队空的情况。
还有一些其他的C++模板操作:
Q.front():即最早被压入队列的元素。
Q.back():即最后被压入队列的元素。
Q.size():返回队列中元素的个数。
队列应用
队列在日常生活中有很多应用,如银行排队系统,餐厅取餐系统,公园售票系统,还有手机短信的发送等等。
1.2.谈谈你对栈和队列的认识及学习体会。
栈和队列都有
2.PTA实验作业
2.1.1 6-5 jmu-ds-舞伴问题
2.1.2代码截图:

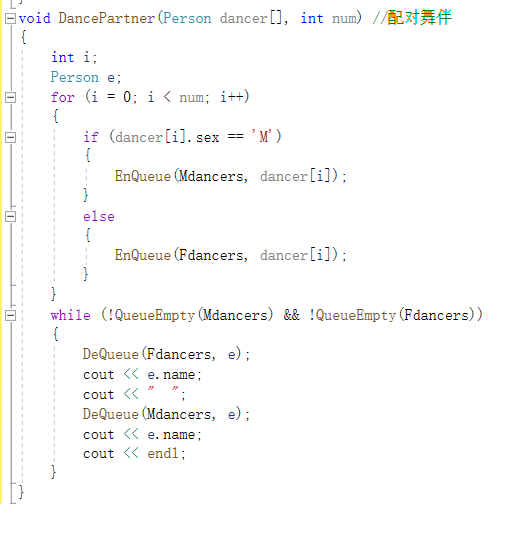
2.1.3 PTA提交列表及说明

编译错误:在VS上用的是C编译,在PTA上用的是C++编译,而且题目的头文件中没有
格式错误:他这个数据之间是两个空格,我第一次提交时只有一个,改过来就可
2.1.1 7-5 表达式转换
2.1.2代码截图
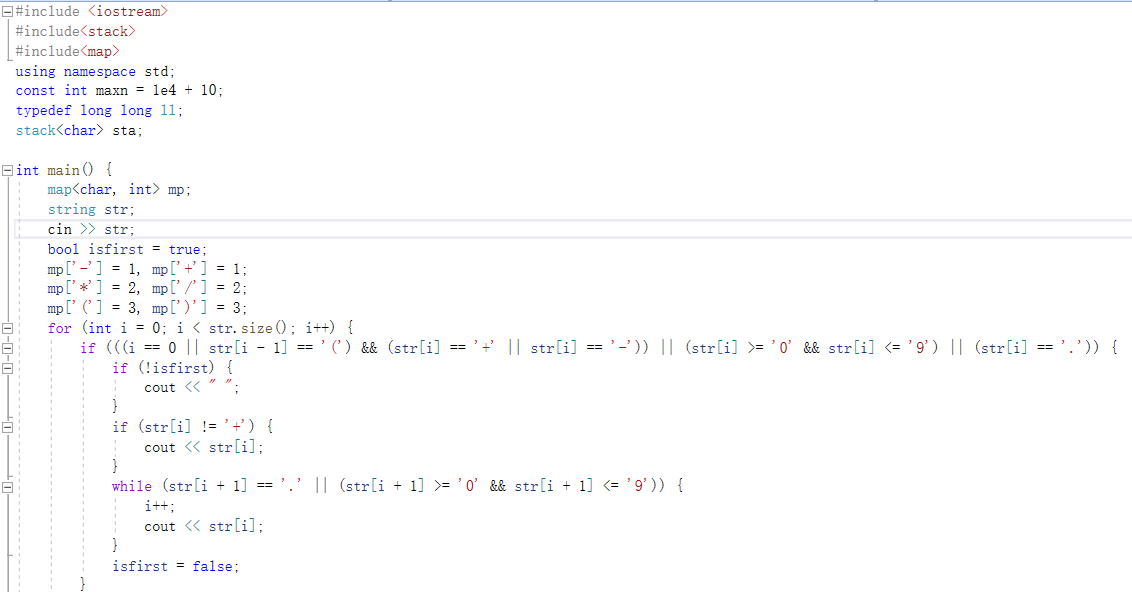

2.1.3本题PTA提交列表说明。


多种错误:第一次没有考虑到有负数的情况,且控制空格输出也写错了
部分正确:更改了输出格式,并加上了负数的情况,但是有嵌套括号的情况还是不对
正确:使用了map容器使得判断条件更为简洁,并修改了一下栈内左括号与栈外括号之间的优先级关系
3.阅读代码(0--4分)
3.1 题目:

代码:
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <stack>
#include <string>
#include <cctype>
using namespace std;
stack <double> st;
int main()
{
string s;
getline(cin, s);
for (int i = s.size() - 1; i >= 0; i--)//取数字
{
if (isdigit(s[i]))
{
double mul = 10, num = s[i] - '0';
for (i--; i >= 0; i--)//再往前一个字符
{
if (isdigit(s[i]))
{
num += (s[i] - '0') * mul;
mul *= 10;//因为是倒着遍历的,这样做使字符串变为数值
}
else if (s[i] == '.')//mul是为了控制小数的
{
num /= mul;
mul = 1;
}
else if (s[i] == '-')//遇到负数直接取相反数
num = -num;
else
break;
}
st.push(num);
}
else if (s[i] != ' ') //else
{
double a, b, sum;
a = st.top();
st.pop();
b = st.top();
st.pop();
switch (s[i])
{
case '+':
sum = a + b;
break;
case '-':
sum = a - b;
break;
case '*':
sum = a * b;
break;
case '/':
{
if (b == 0)
{
cout << "ERROR";
return 0;
}
sum = a / b;
}
}
st.push(sum);
}
}
printf("%.1lf", st.top());
}
3.1.1 该题的设计思路
首先从右向左开始入栈,当遇到第一个操作符的时候出栈两次计算结果,再将结果入栈,最后输出总结果
由于是前缀表达式,所以必然是先有运算符,再有两个数字的,所以我们从后往前遍历,24-45行代码是读取一个数字的,每读完一个数字就压入栈中,当读到运算符时,就将栈顶的两个元素取出st.top()并删除这两个元素st.pop(),然后计算值并将值压入栈中以便下次计算st.push(sum),注意一个小问题,46行写成else if,原因自己想想就知道了。
函数说明:
isdigit(s[i]);//判断s[i]是否是0-9的阿拉伯数字,在头文件#include
getline(cin, s);//将字符串读入到s中,在头文件#include
扩展:cin.get()获取一个字符;getline(cin,s)是C的,获取一行字符串;cin.getline() 获取一行字符串,可以接收空格并输出
3.1.2 该题的伪代码
int main()
{
定义类型为double的栈
定义数组s
将数据读入到数组s中
for(倒着遍历字符数组)
{
if(为数字)
{
for(遍历接下去的一个字符)
{
根据情况将字符串转化为数值
直到一个"数字"结束,break;
}
数值入栈;
}
else if(为运算符)
{
取出栈最上面的两个数字
根据运算符计算
在将结果压入栈中
}
}
输出栈顶元素
}
3.1.3 运行结果

3.1.4分析该题目解题优势及难点。
1、题目中没有明确说明是整数,而且也没说是正数,所以我们必须考虑 小数 和 负数 的情况 !
2、因为是按字符输入,例如小数3.2 的格式为3.2,这里‘.’的前后是没有空格的!我们读取从右至左,所以会先读到2然后是‘.’,最后是3;我们只需要让2变成0.2;加上3就搞定了!!!
3、负数:例如-1 格式是就是-1 中间也没有空格;有空格一定是-。我们遍历时如果遇到数字和‘-’挨着,那么就一定是负数!!!
3.2题目:

代码:
#include<iostream>
#include<set>
using namespace std;
int main()
{
int num, n;
cin >> n;
set<int> s;
for (int i = 0; i < n; i++)
{
cin >> num;
if (s.upper_bound(num) != s.end())
s.erase(s.upper_bound(num));
s.insert(num);
}
cout << s.size() << endl;
return 0;
}
3.2.1 该题的设计思路
先将一个数插入进set容器中,set容器默认从小到大(自动排序),在依次进行每个数的输入,如果输入的数比当前set容器中的最后一个数小,删除set容器中第一个大于输入数的值,在将输入数进行插入,重新排序后,输入的值就代替了删除的值,依次循环往复,进行到结尾 。
函数说明:
rbegin():
c.begin() 返回一个迭代器,它指向容器c的第一个元素
c.end() 返回一个迭代器,它指向容器c的最后一个元素的下一个位置
c.rbegin() 返回一个逆序迭代器,它指向容器c的最后一个元素
c.rend() 返回一个逆序迭代器,它指向容器c的第一个元素前面的位置
upper_bound():
upper_bound是找到大于t的最小地址,如果没有就指向末尾
lower_bound是找到大于等于t的最小地址
set::erase():
erase() 迭代器的参数必须是一个指向容器中元素的、有效的、可解引用的迭代器,因此需要确保它不是容器的结束迭代器。这个版本的 erase() 函数会返回一个指向被删除元素的下一个位置的迭代器,如果删除的是最后一个元素,那么它就是结束迭代器。
调用unordered_set容器的成员函数clear()可以删除它的全部元素。成员函数erase()可以删除容器中和传入参数的哈希值相同的元素。另一个版本的erase()函数可以删除迭代器参数指向的元素。
3.2.2 伪代码
int main()
{
读取列车的序列数
set一个容器s
在依次进行每个数的输入
if(输入的数比当前set容器中的最后一个数小)
删除set容器中第一个大于输入数的值,
再将输入数进行插入
输出s的长度
}
3.2.3 运行结果




