DS博客作业02--线性表
0.PTA得分截图

1.本周学习总结
1.1 线性表
· 顺序表结构体
typedef int ElemType;
typedef struct
{
ElemType data[MaxSize]; //存放顺序表元素
int length ; //存放顺序表的长度
} List;
· 创建循序表
void CreateList(SqList& L, int n)//构建顺序表函数 ,n为顺序表长度
{
L = new List;
L->length = n;
for (int i = 0; i < n; i++)
{
cin >> L->data[i];
}
}
· 顺序表插入
bool Insert(List L, ElementType X, Position P)//X表示要插入的元素,P表示插入位置
{
if (L->Last + 1 == MAXSIZE)//顺序表已满
{
printf("FULL");
return false;
}
int i;
if (P<0 || P>(L->Last + 1))
{
return false;//位置非法
}
for (i = L->Last; i >= P; i--)
{
L->Data[i + 1] = L->Data[i];
}
L->Data[P] = X;
L->Last++;//最后一个位置下标++
return true;
}
· 顺序表删除
bool Delete(List L, Position P)//P表示要插入的位置
{
if (P<0 || P>(L->Last + 1))//非法访问
{
return false;
}
int i;
for (i = P; i <= L->Last-1; i++)
{
L->Data[i] = L->Data[i + 1];//从第i个元素开始,之后的元素往前移
}
L->Last--;//最后一个位置的下标--
return true;
}
· 单链表结构体定义
typedef struct LNode //定义单链表结点类型
{
ElemType data;
struct LNode *next;//指向后继结点
} LNode,*LinkList;
· 两种建立链表的方式
(1)尾插法
void CreateList(LinkList& L, int n)
{
LinkList tail, p;
L = new LNode;
tail = L;
L->next=NULL;
for (int i = 0; i < n; i++)
{
p = new LNode;
cin >> p->data;
p->next = NULL;
tail->next = p;
tail = p;
}
}
图解:
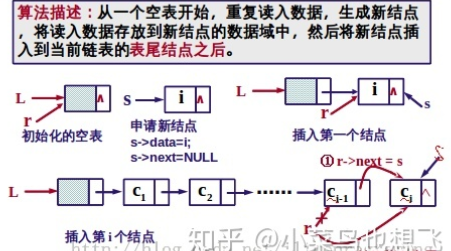
(2)头插法
void CreateListF(LinkList& L, int n)
{
LinkList pre;
L = new LNode;
L->next = NULL;
ElemType i;
for ( i = 0; i < n; i++)
{
pre = new LNode;
cin >> pre->data;
pre->next = L->next;
L->next = pre;
}
}
图解:
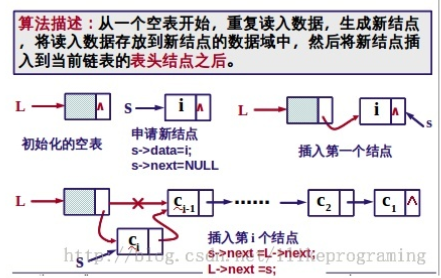
· 有序单链表插入删除
(1)插入数据
void ListInsert(LinkList& L, ElemType e)
{
LinkList p,pre;
p = new LNode;
p->data = e;
pre = L;
while (pre->next)
{
if (pre->next->data > e)//找到第一个比要插入数据大的数
{
p->next = pre->next;
pre->next = p;
return;
}
else pre = pre->next;
}
p->next = pre->next;//若插入数据最大则插在最后
pre->next = p;
}
(2)删除数据
void ListDelete(LinkList& L, ElemType e)
{
if (L->next == NULL)return;
LinkList p, pre;
pre = L;
while (pre->next)
{
if (pre->next->data == e)//遍历链表找到要删除目标位置
{
p = pre->next;
pre->next = p->next;
delete p; return;
}
else pre = pre->next;
}
cout <<e<< "找不到!"<<endl;//删除要考虑找不到的情况
}
· 合并两个单链表
void MergeList(LinkList& L1, LinkList L2)//合并链表,使合并后的链表非降排列
{
LinkList p = L1->next, q = L2->next, L3, r, node;
r = new LNode;
r->next = NULL;
L3 = r;
while (p && q)//同时遍历
{
if (p->data > q->data)
{
node = q;
q = q->next;//指针下移
node->next = NULL;
r->next = node;
r = node;
}
else if (p->data < q->data)
{
node = p;
p = p->next;//指针后移
node->next = NULL;
r->next = node;
r = node;
}
else
{
node = p;
q = q->next;
p = p->next;//两个指针同时后移
node->next = NULL;
r->next = node;
r = node;
}
}
if (p)r->next = p;
if (q)r->next = q;
L1 = L3;
}
· 循环链表
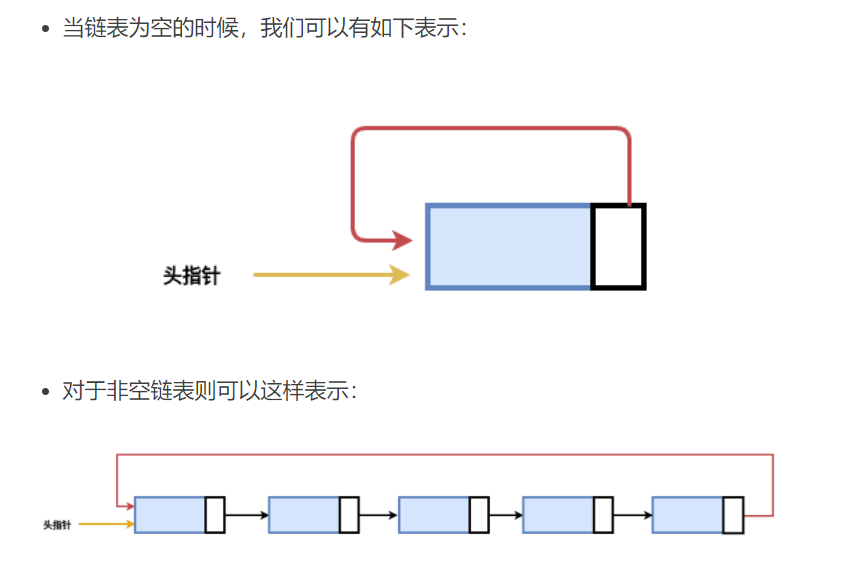
对于循环链表这种设计,我们在遍历的时候的结束条件就不再是p为空的时候结束了。而是!!p等于头结点!!的时候遍历才完成。
· 双向链表

1.2学习体会
顺序表还好,链表要特别小心p和p->next是否为空,还有其他的next关系,学习链表要从基础的开始,先把链表建好,熟悉头插和尾插,在掌握其他操作如插入,删除,逆序,合并等,此外还可以了解一些C++对于链表常用的库函数,如vector和algorithm里的一些和顺序表操作有关的函数。

2.PTA实验作业
2.1 题目:6-11 链表分割
2.1.1 代码截图

2.1.2 PTA提交列表及说明

2.2题目:6-8 链表倒数第m个数
2.2.1 代码截图

2.2.2 PTA提交列表及说明

2.3题目:7-1 两个有序序列的中位数、
2.3.1 代码截图

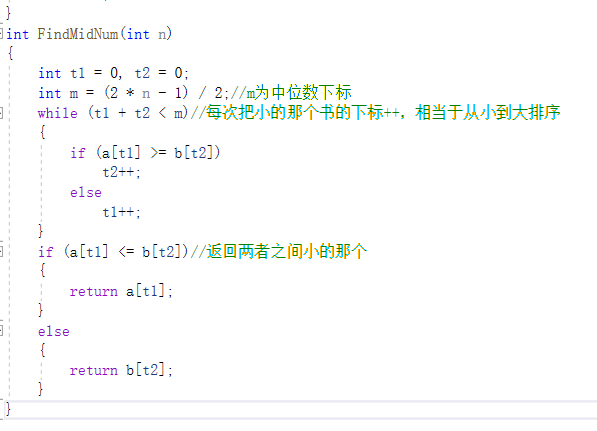
2.3.2 PTA提交列表及说明
3.阅读代码
3.1
问题:

代码如下:
法一:
#include<iostream>
#include<algorithm>
using namespace std;
int N,W;
const int maxn=105;
int v[maxn],w[maxn];
int rec(int i,int j)//从第i个下标开始,计算剩余j重量怎么挑选商品
{
int ans;
if(i==N) ans=0;//已经没有商品可以选择,递归出口。
else if(j<w[i]) ans=rec(i+1,j);//如果背包容量装不下下标为i的商品
else ans=max(rec(i+1,j),rec(i+1,j-w[i])+v[i]);/*方程由来:http://blog.sina.com.cn/s/blog_e65dd0270102wd9k.html*/
return ans;
}
int main()
{
cin>>N>>W;
for(int i=0;i<N;i++) cin>>w[i];
for(int i=0;i<N;i++) cin>>v[i];
int res=rec(0,W);
cout<<res<<endl;
return 0;
}
这种算法是对每个商品都进行处理,每一层搜索都有两个分支,时间复杂度为O(2^n),当n比较大的时候就会花费较多的时间。
对每个商品进行搜索的时候,有时会出现相同的参数,于是第二次调用的时候我们其实已经计算过一次了,等于是白白浪费了时间。
···
法二:
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int maxN=3405;
const int maxW=405;
int dp[maxN][maxW];
int N,W;
int w[maxW],v[maxN];
int rec(int i,int j){
if(dp[i][j]>=0) return dp[i][j];
int ans;
if(i==N) ans=0;
else if(j<w[i]) ans=rec(i+1,j);
else ans=max(rec(i+1,j),rec(i+1,j-w[i])+v[i]);
return dp[i][j]=ans;
}
int main(){
memset(dp,-1,sizeof(dp));
cin>>N>>W;
for(int i=0;i<N;i++)
{
cin>>w[i];
cin>>v[i];
}
int res=rec(0,W);
cout<<res<<endl;
return 0;
}
dp[][]为记忆数组,用于记录下之前每一次的结果。我们如果把dp[i][j]定义成如下意义:当总重量小于j时,从下标为i的商品开始挑选,得到商品的最大值。于是有下面的递推公式:

法三:
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int maxN=3405;
const int maxW=405;
int dp[maxN][maxW];
int N,W;
int w[maxW],v[maxN];
void solve(){
for(int i=N-1;i>=0;i--){
for(int j=0;j<=W;j++){
if(j<w[i])
dp[i][j]=dp[i+1][j];
else
dp[i][j]=max(dp[i+1][j],dp[i+1][j-w[i]]+v[i]);
}
}
cout<<dp[0][W]<<endl;
}
int main()
{
cin>>N>>W;
for(int i=0;i<N;i++)
{
cin>>w[i];
cin>>v[i];
}
solve();
return 0;
}



