bzoj2286

虚树+树形dp

虚树一类问题是指多次询问，每次询问的点数较少，如果我们每次都对整棵树进行遍历，那么自然是不行的，这时我们就构造出一棵虚树来降低复杂度

具体构建就是把一些无用的点缩起来。我们考虑对于一个点包括自己和这个点的子树，我们怎么构建虚树。

我们把所有点按dfs序排序，也就是模拟出dfs的过程，然后用一个栈维护。

每次加入新点x，我们求出和栈顶y的lca,t,如果dfn[t]>=dfn[y],那么说明x在y的下面，那么直接入栈就行了，否则就不在同一条子树的链中，这时我们就要像dfs一样退栈，这时要注意

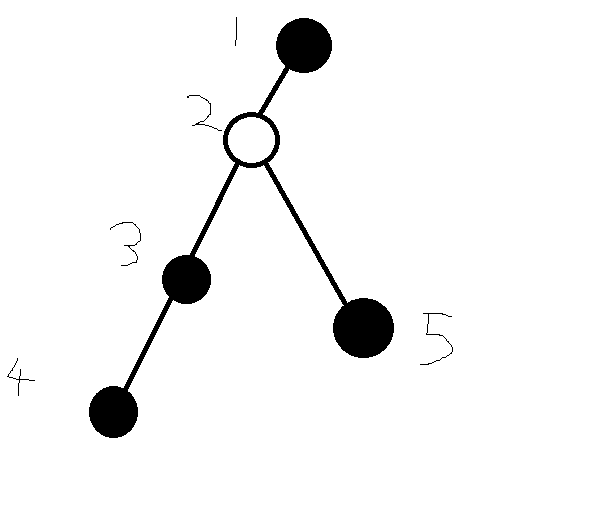
黑点是需要构建的点，当我们加入4号点时，栈里有1,3,4,加入5的时候，我们发现需要退栈，我们先弹掉4,把3->4连边，然后就需要注意，我们不能把1->3,而需要把2->3,于是我们判断dfn[lca]和dfn[st[top-1]]的大小关系来决定如何连边，再把3弹掉，然后如果栈顶不是lca,那么就把lca=2加入栈里，继续进行这个过程

最后就是树形dp了

其实虚树的构建很像dfs的过程

#include<cstdio>
#include<cstring>
#include<algorithm>
#include<vector>
#include<iostream>
using namespace std;
const int N = 250010;
struct edge {
    int nxt, to;
    long long w;
} e[N << 1];
int n, m, cnt = 1, tot, top;
int head[N], dfn[N], dep[N], fa[N], Top[N], size[N], a[N], st[N], mark[N], son[N];
long long val[N];
vector<int> G[N];
namespace IO 
{
    const int Maxlen = N * 50;
    char buf[Maxlen], *C = buf;
    int Len;
    inline void read_in()
    {
        Len = fread(C, 1, Maxlen, stdin);
        buf[Len] = '\0';
    }
    inline void fread(int &x) 
    {
        x = 0;
        int f = 1;
        while (*C < '0' || '9' < *C) { if(*C == '-') f = -1; ++C; }
        while ('0' <= *C && *C <= '9') x = (x << 1) + (x << 3) + *C - '0', ++C;
        x *= f;
    }
    inline void fread(long long &x) 
    {
        x = 0;
        long long f = 1;
        while (*C < '0' || '9' < *C) { if(*C == '-') f = -1ll; ++C; }
        while ('0' <= *C && *C <= '9') x = (x << 1ll) + (x << 3ll) + *C - '0', ++C;
        x *= f;
    }
    inline void read(int &x)
    {
        x = 0;
        int f = 1; char c = getchar();
        while(c < '0' || c > '9') { if(c == '-') f = -1; c = getchar(); }
        while(c >= '0' && c <= '9') { x = (x << 1) + (x << 3) + c - '0'; c = getchar(); }
        x *= f;
    }
    inline void read(long long &x)
    {
        x = 0;
        long long f = 1; char c = getchar();
        while(c < '0' || c > '9') { if(c == '-') f = -1; c = getchar(); }
        while(c >= '0' && c <= '9') { x = (x << 1ll) + (x << 3ll) + c - '0'; c = getchar(); }
        x *= f;
    } 
} using namespace IO;
int lca(int u, int v)
{
    while(Top[u] != Top[v])
    {
        if(dep[Top[u]] < dep[Top[v]]) swap(u, v);
        u = fa[Top[u]];
    }
    return dep[u] < dep[v] ? u : v;
}
void dfs(int u, int last)
{
    size[u] = 1;
    for(int i = head[u]; i; i = e[i].nxt) if(e[i].to != last)
    {
        dep[e[i].to] = dep[u] + 1;
        fa[e[i].to] = u;
        val[e[i].to] = min(val[u], e[i].w);
        dfs(e[i].to, u);
        size[u] += size[e[i].to]; 
        if(size[e[i].to] > size[son[u]]) son[u] = e[i].to;
    }
}
void dfs(int u, int acs, int last)
{
    dfn[u] = ++tot;
    Top[u] = acs;
    if(son[u]) dfs(son[u], acs, u);
    for(int i = head[u]; i; i = e[i].nxt) if(e[i].to != last && e[i].to != son[u]) dfs(e[i].to, e[i].to, u);
}
void link(int u, int v, long long w)
{
    e[++cnt].nxt = head[u];
    head[u] = cnt;
    e[cnt].to = v;
    e[cnt].w = w;
}
bool cp(int i, int j) { return dfn[i] < dfn[j]; }
long long dfs(int u)
{
    long long ret = 0;
    for(int i = 0; i < G[u].size(); ++i)
    {
        int v = G[u][i];
        ret += dfs(v);
    }
    G[u].clear();
    if(mark[u]) return val[u];
    else return min(ret, val[u]);
}
void solve()
{
    fread(n);
    for(int i = 1; i <= n; ++i) fread(a[i]), mark[a[i]] = 1;
    sort(a + 1, a + n + 1, cp);
    top = 0;
    st[++top] = 1;
    for(int i = 1; i <= n; ++i)
    {
        int grand = lca(a[i], st[top]);
        while(dfn[grand] < dfn[st[top - 1]] && top > 1) G[st[top - 1]].push_back(st[top]), --top;
        if(dfn[st[top]] > dfn[grand]) G[grand].push_back(st[top]), --top;
        if(st[top] != grand) st[++ top] = grand;
        st[++ top] = a[i];
    }
    for(int i = top; i > 1; --i) G[st[i - 1]].push_back(st[i]); 
    printf("%lld\n", dfs(st[1]));
    for(int i = 1; i <= n; ++i) mark[a[i]] = 0;
}
int main()
{
    read_in();
    fread(n);
    for(int i = 1; i < n; ++i)
    {
        int u, v;
        long long w;
        fread(u);
        fread(v);
        fread(w);
        link(u, v, w);
        link(v, u, w);
    }
    val[1] = 1ll << 60;
    dfs(1, 0);
    dfs(1, 1, 0);
    fread(m);
    while(m --) solve();
    return 0;
}