123D

后缀数组+单调栈

看了好长时间，最后看了张神的程序才搞懂

意思就是求所有子串*n*(n+1)/2 n是子串出现次数

 

事实上，lcp可以看成宽度为1，高度为lcp值的长方形，所有lcp放在一起就是一堆长方形放在一起，然后我们就要求对于每个高度对应的长方形的面积乘上一个值

每个长方形可以用单调栈求，也就是一个高度能最远延伸到哪里，单调栈维护当前长方形的高度递增。

 

比如说这个样子，

不满足单调性了，

 

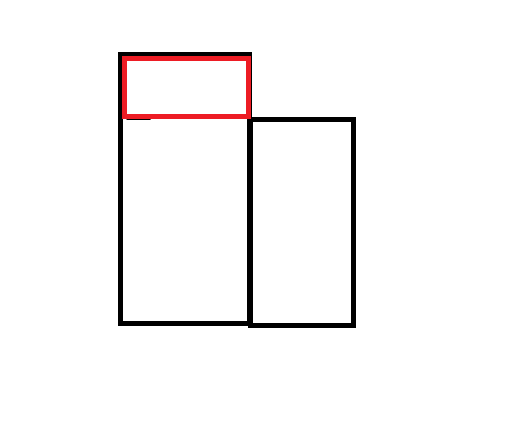
 这段红色的区间就要截掉

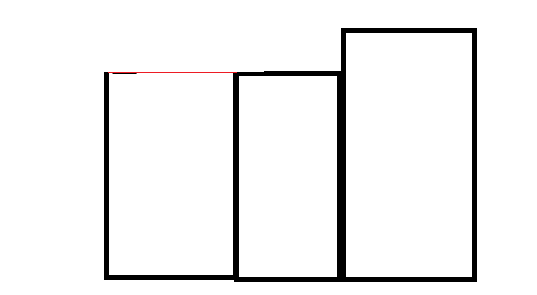
进来一个比较高的不用管

 

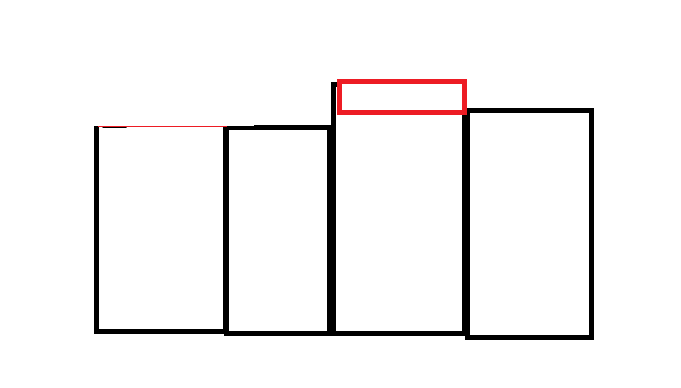
进来一个比较小的删掉红的

 

 

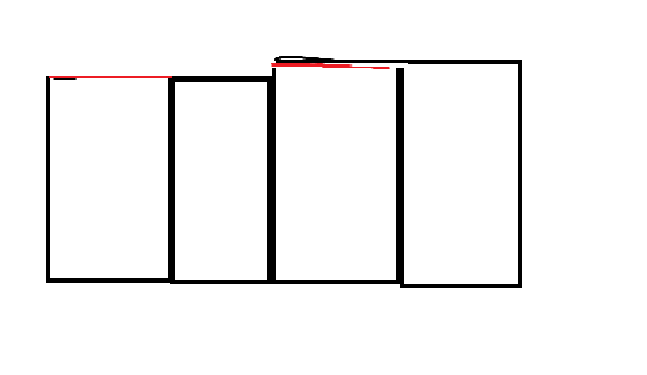
 变成了这个样子

 

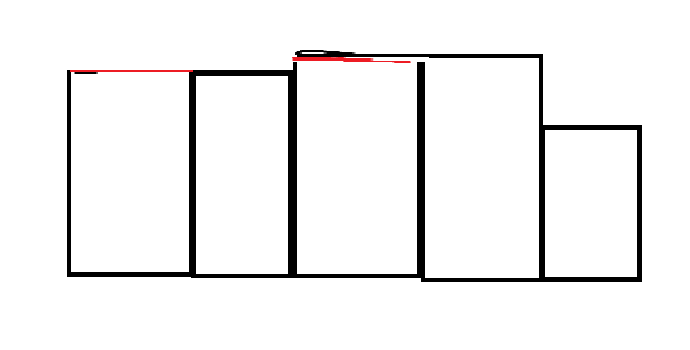
进来一个很小的

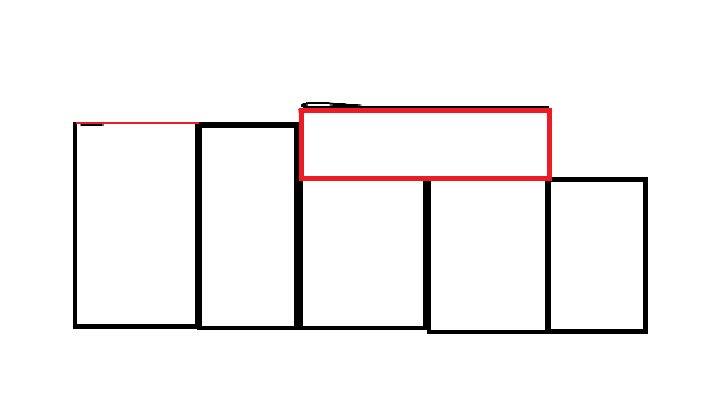
先把红色删掉

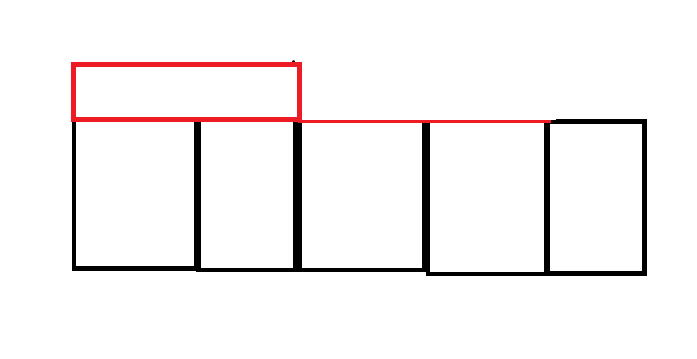
再把这块删掉，于是栈里又是不递增的了

最后我们把一个高度为0的lcp放入栈中，就把所有长方形加到答案里了。

还有一种情况，自己和自己也要加入答案，那么我们先把这个算掉再放入栈中。

做后缀数组要把所有和lcp无关的东西都砍掉，像自己和自己的答案应该单独统计，lcp有关的一起算，这样会方便很多

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define N 500010
ll ans;
int n,k, top;
char s[N];
int Rank[N],sa[N],temp[N],lcp[N],st[N][2],l[N],r[N];
inline bool cp(int i,int j)
{
    if(Rank[i]!=Rank[j]) return Rank[i]<Rank[j];
    int ri=i+k<=n?Rank[i+k]:-1;
    int rj=j+k<=n?Rank[j+k]:-1;
    return ri<rj;
}
void Sa()
{
    for(int i=1;i<=n;++i)
    {
        Rank[i]=s[i]; sa[i]=i;
    }
    for(k=1;k<=n;k<<=1)
    {
        sort(sa+1,sa+n+1,cp);
        temp[sa[1]]=1;
        for(int i=2;i<=n;++i) temp[sa[i]]=temp[sa[i-1]]+(cp(sa[i-1],sa[i]));
        for(int i=1;i<=n;++i) Rank[i]=temp[i];
    }
}
void Lcp()
{
    for(int i=1;i<=n;++i) Rank[sa[i]]=i;
    int h=0;
    for(int i=1;i<=n;++i)
    {
        if(Rank[i]<=1) continue;
        int j=sa[Rank[i]-1];
        if(h>0) --h;
        for(;i+h<=n&&j+h<=n;++h) if(s[i+h]!=s[j+h]) break;
        lcp[Rank[i]]=h;
    }
}
ll mul(ll x)
{
    return x * (x + 1ll) / 2ll;
}
int main()
{
    scanf("%s",s+1);
    n = strlen(s + 1);
    Sa();
    Lcp();
    for(int i = 1; i <= n; ++i)
    {
        ans += (ll)(n - sa[i] + 1) - max(lcp[i], lcp[i + 1]);
        int left = i;
        while(top && lcp[i + 1] < st[top][1])
        {
            ans += mul(i - st[top][0] + 1) * (st[top][1] - max(st[top - 1][1], lcp[i + 1]));
            left = st[top][0];
            --top;
        }
        ++top;
        st[top][0] = left;
        st[top][1] = lcp[i + 1];
    }
    printf("%lld\n", ans);
    return 0;
}