java第二章作业
1.(1)使用组合数公式利用n!来计算
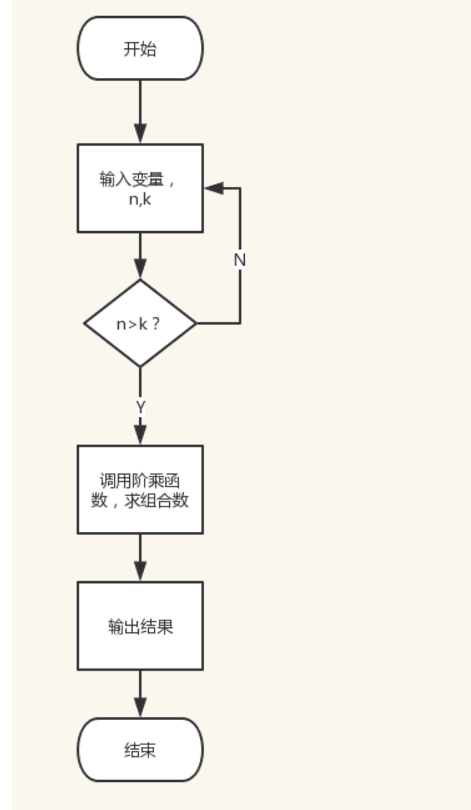
设计思想:先解决求n!的函数,再结合组合数公式,求组合数
程序流程图:
源代码:
package Test;
import java.util.*;
public class Zuheshu {
public static void main(String[] args) {
Scanner in = new Scanner(System.in
);
System.out.print("输入组合数下标n:");
int n = in.nextInt();
System.out.print("输入组合数上标k:");
int k = in.nextInt();
int C = Jiecheng(n)/(Jiecheng(k)*Jiecheng(n - k));
System.out.println("C(n,k) = "+C);
}
public static int Jiecheng(int n)
{
int s = 0;
if(n < 0)
System.out.println("Error!");
else if(n == 1||n == 0)
s = 1;
else
s = n * Jiecheng(n -1);
return s;
}
}
结果截图:

(2)使用递推的方法用杨辉三角形计算
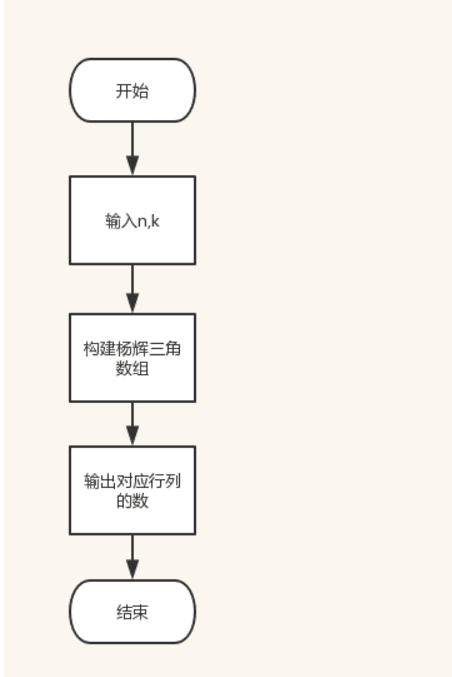
设计思想 : 构建杨辉三角 ,组合数结果就相当于杨辉三角中的一个数,n为行,k为列 输出相应的数就可以
程序流程图:
源代码:
package Test;
import java.util.Scanner;
public class yanghui {
public static void main(String args[])
{
Scanner input=new Scanner(System.in);
int n,k;
System.out.println("输入组合数公式的n,k:");
n=input.nextInt();
k=input.nextInt();
int [][]f=new int[27][27];
f[0][0] = 1;
for(int i = 1;i <= 24;i++)
{
for(int j = 1;j <= i + 1;j++)
{
f[i][j] = f[i - 1][j - 1] + f[i - 1][j];
}
}
System.out.println("结果为"+f[n+1][k+1]);
}
}
(3). 使用递归的方法用组合数递推公式计算
设计思想 : 递归组合数,相当于杨辉三角 构建递归函数,n,k相应于杨辉三角的行列
程序流程图:
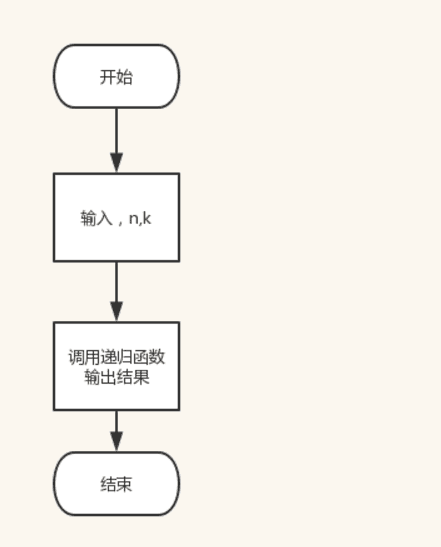
源代码:
package Test;
import java.util.Scanner;
public class TextRandom {
public static void main(String args[])
{
Scanner input=new Scanner(System.in);
int n,k;
System.out.println("请输入组合数公式的n和k:");
n=input.nextInt();
k=input.nextInt();
System.out.println("组合结果为"+ZuHe(n,k));
}
public static long ZuHe(int a,int b)
{
if(b==0)return 1;
else {
if(a==1)return 1;
else {
if(a==b)return 1;
else {
return (ZuHe(a-1,b-1)+ZuHe(a-1,b));
}
}
}
}
}

2.递归编程解决汉诺塔问题.
设计思想:从主线程开始调用函数进行不停的压栈和出栈操作,函数的调用就是将函数压如栈中,函数的结束就是函数出栈的过程,这样就保证了方法调用的顺序流,即当函数出现多层嵌套时,需要从外到内一层层把函数压入栈中,最后栈顶的函数先执行结束(最内层的函数先执行结束)后出栈,再倒数第二层的函数执行结束出栈,到最后,第一个进栈的函数调用结束后从栈中弹出回到主线程,并且结束。
源代码:
package Test;
import java.util.Scanner;
public class demo {
static int m =0;//标记移动次数
//实现移动的函数
public static void move(int disks,char N,char M)
{
System.out.println("第" + (++m) +" 次移动 : " +" 把 "+ disks+" 号圆盘从 " + N +" 移到 " + M);
}
//递归实现汉诺塔的函数
public static void hanoi(int n,char A,char B,char C)
{
if(n == 1)//圆盘只有一个时,只需将其从A塔移到C塔
demo.move(1, A, C);//将编号为1的圆盘从A移到C
else
{
hanoi(n - 1, A, C, B);//递归,把A塔上编号1~n-1的圆盘移到B上,以C为辅助塔
demo.move(n, A, C);//把A塔上编号为n的圆盘移到C上
hanoi(n - 1, B, A, C);//递归,把B塔上编号1~n-1的圆盘移到C上,以A为辅助塔
}
}
public static void main(String[] args) {
Scanner imput = new Scanner(System.in);
char A = 'A';
char B = 'B';
char C = 'C';
System.out.print("请输入圆盘的个数:");
int disks = imput.nextInt();
demo.hanoi(disks, A, B, C);
System.out.println(">>一共移动了" + m + "次");
imput.close();
}

3.使用递归方式判断某个字串是否是回文
设计思想: 从开头开始依次比较首尾字符 ,如果相同,再比较第二个字符和倒数第二个 ,依次比较直到最后完全相同,输出
程序流程图:
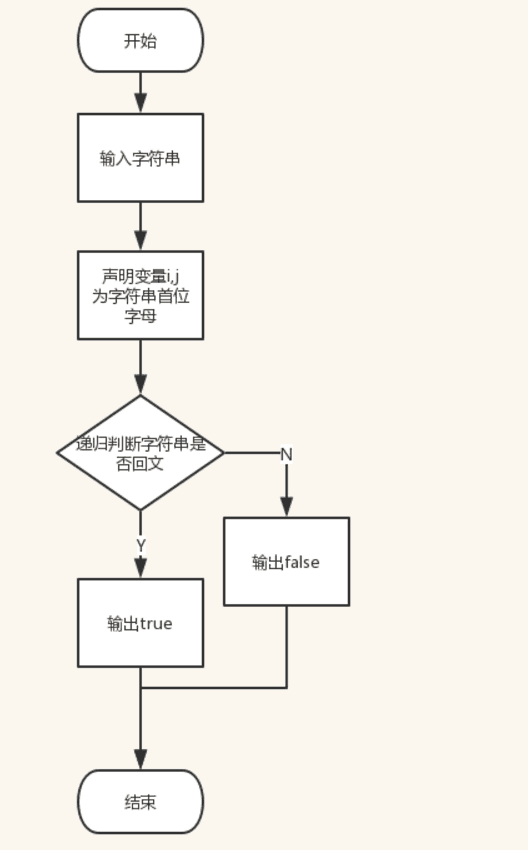
源代码:
package Test;
import java.io.BufferedReader;
import java.io.InputStreamReader;
public class HuiWen {
public static void main(String[] args)throws Exception {
String str ="";
BufferedReader br = new BufferedReader(
new InputStreamReader(System.in),256);
System.out.println("请输入一串字符,每个字或单词用空格隔开:");
str = br.readLine();
System.out.println("检查结果: " + huiwen(str,0,str.length()-1));
}
public static boolean huiwen(String s,int start,int end){
if(start == end) return true;
if(start > end){
System.out.println("输入有误!");
return false;
}
if(s.charAt(start) == s.charAt(end)){
return huiwen(s,start+1,end-1);
}
else{
return false;
}
}
}