CF1279F New Year and Handle Change 题解

来翻译一下 cf 评论区一老哥的证明。

首先问题可以转化为选出 \(k\) 个长为 \(l\) 的区间使得覆盖的 \(1\) 个数最多。

不妨设 \(kl\le n\)，设选 \(k\) 个区间最多能覆盖 \(f_k\) 个 \(1\)，显然存在一种最优方案使得区间两两不交。

下面证明 \(f_{k+1}\ge \frac{f_{k}+f_{k+2}}{2}\)，即 \(f\) 具有凸性。

分别找到 \(k\) 时和 \(k+2\) 时的一组最优解：

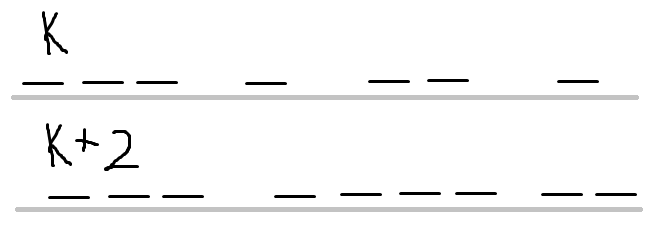
把相交的区间对应连边，如图：

形成了若干连通块，每个连通块内 \(k\) 和 \(k+2\) 的区间数之差不超过 \(1\)，因此必然有一个连通块在 \(k+2\) 中的区间数比在 \(k\) 中的区间数多 \(1\)，翻转这个连通块：

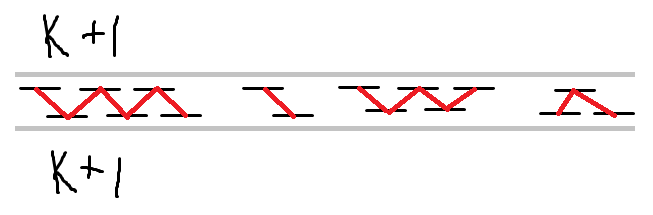
于是得到了两种 \(k+1\) 时的方案，取更优的那组即可，得证。

证明了凸性后就是 wqs 二分的板子题了，时间复杂度 \(O(n\log n)\)。

Code

#include<bits/stdc++.h>
#define LL long long
using namespace std;
int n,l,L,R,mid,t;
LL m,ans;
int a[1000002];
LL f[1000002],g[1000002];
char ch[1000002];
template<class T>void read(T &x)
{
	x=0;int f=0;char ch=getchar();
	while(ch<'0' || ch>'9')f|=(ch=='-'),ch=getchar();
	while(ch>='0' && ch<='9')x=(x<<3)+(x<<1)+(ch^48),ch=getchar();
	x=f? -x:x;return ;
}
inline bool check(int o)
{
	t=0;
	for(int i=0;i<l;++i)f[i]=g[i]=0;
	for(int i=l;i<=n;++i)
	{
		if(f[i-l]<f[t] || (f[i-l]==f[t] && (o? g[i-l]>g[t]:g[i-l]<g[t])))t=i-l;
		f[i]=f[t]+a[i-l]+mid,g[i]=g[t]+1;
		if(f[i-1]+a[i]<f[i] || (f[i-1]+a[i]==f[i] && (o? g[i-1]>g[i]:g[i-1]<g[i])))f[i]=f[i-1]+a[i],g[i]=g[i-1];
		f[i]-=a[i];
	}
	if(o || g[n]<=m)ans=min(ans,f[n]+a[n]-min(g[n],m)*mid);
	return g[n]<=m;
}
inline void solve(int c)
{
	for(int i=1;i<=n;++i)a[i]=a[i-1]+(ch[i]!=c);
	for(L=0,R=n;L<=R;)
	{
		mid=((L+R)>>1);
		if(check(0))R=mid-1;
		else L=mid+1;
	}
	mid=L,check(1);
}
int main()
{
	read(n),read(m),read(l);
	if(1LL*m*l>=n)return 0&puts("0");
	scanf("%s",ch+1),ans=n;
	for(int i=1;i<=n;++i)ch[i]=(ch[i]<='Z');
	solve(0),solve(1);
	return 0&printf("%lld",ans);
}