CF573D Bear and Cavalry 题解
wangyo Orz!
题意
有 \(n\) 个人和 \(n\) 匹马,第 \(i\) 个人对应第 \(i\) 匹马,第 \(i\) 个人能力值为 \(w_i\),第 \(i\) 匹马能力值为 \(h_i\),第 \(i\) 个人骑第 \(j\) 匹马的总能力值为 \(w_i\times h_j\),整个军队的总能力值为 \(\sum w_i\times h_j\)(一个人只能骑一匹马,一匹马只能被一个人骑)。每个人都不能骑自己对应的马,制定骑马方案使整个军队的总能力值最大。现在有 \(q\) 个操作,每次给出 \(a,b\),交换 \(a\) 和 \(b\) 对应的马,每次操作后都输出最大的总能力值。
题解
目前网上所有题解包括官方题解都没有第二个结论的证明,所以这篇题解主要是来补证明的。
结论 \(1\):把 \(w,h\) 排序后,第 \(i\) 个人匹配的马必定在 \([i-2, i+2]\) 中。
证明:见 _sys 的题解。
结论 \(2\):在一种最优匹配中,只有三种可能的匹配类型:第 \(i\) 个人与第 \(i\) 匹马匹配;第 \(i,i-1\) 个人与第 \(i,i-1\) 匹马匹配;第 \(i,i-1,i-2\) 个人与第 \(i,i-1,i-2\) 匹马匹配。
证明:如果 \([i,i+k]\) 内的人和马能够内部完全匹配,则称其为一个长度为 \(k-i+1\) 的连续段。该结论等价于证明存在最优方案满足其中所有连续段长度都不超过 \(3\)。
考虑反证,即假设所有最优方案中都存在长度超过 \(3\) 的连续段,那么我们证明对每一段长度超过 \(3\) 的连续段都可以通过调整使其变为若干长度不超过 \(3\) 的连续段且答案不会变劣。
由结论 \(1\) 可以发现,对于长度超过 \(3\) 的连续段,只有如下两种类型。
第一类:
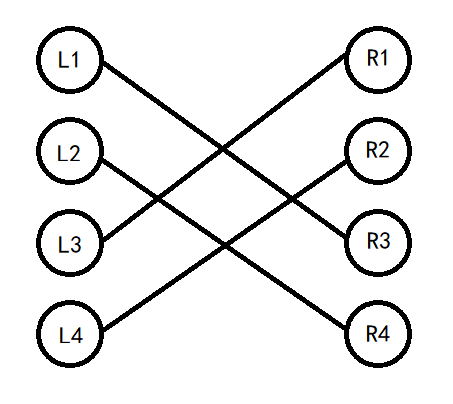
这种情况只有连续段的长度为 \(4\) 时才可能出现。
由于已经是最优方案了,所以所有逆序对都无法直接调整使其消失,那么可以列出一些限制:
L1 与 R1 是同组的或 L3 与 R3 是同组的。
L2 与 R2 是同组的或 L4 与 R4 是同组的。
L1 与 R2 是同组的或 L4 与 R3 是同组的。
L2 与 R1 是同组的或 L3 与 R4 是同组的。
图中连的边的两端点都不是同组的。
于是列个表就可以发现一定能找到更优的符合条件的方案。
第二类:
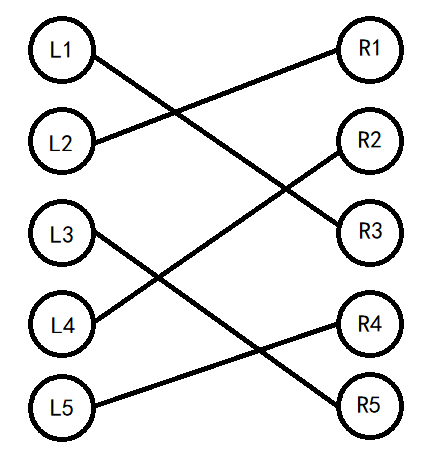
注意这种情况是可以无限延伸的,即对于任意 \(i\ge4\),都能找到一种类似的情况,所以我们考虑归纳证明。
-
L1 与 R2 不同组,L4 与 R3 不同组,那么可以将 L1-R3,L4-R2 调整为 L1-R2,L4-R3。将一个长度为 \(n\) 的连续段拆成了一个长度为 \(2\) 和一个长度为 \(n-2\) 的连续段。
-
L1 与 R2 同组,L4 与 R3 不同组,那么可以将 L1-R3,L2-R1,L4-R2 调整为 L1-R1,L2-R2,L4-R3。将一个长度为 \(n\) 的连续段拆成了两个长度为 \(1\) 和一个长度为 \(n-2\) 的连续段。
-
L1 与 R2 不同组,L4 与 R3 同组,那么可以将 L1-R3,L3-R5,L4-R2 调整为 L1-R2,L3-R3,L4-R5。将一个长度为 \(n\) 的连续段拆成了一个长度为 \(1\),一个长度为 \(2\) 和一个长度为 \(n-3\) 的连续段。
-
L1 与 R2 同组,L4 与 R3 同组,那么可以将 L1-R3,L2-R1 调整为 L1-R1,L2-R3。将一个长度为 \(n\) 的连续段拆成了一个长度为 \(1\) 和一个长度为 \(n-1\) 的连续段。
上述所有情况都能通过调整使其变为若干长度更短的连续段且答案不会变劣,所以由归纳法得证。
有了结论 \(2\) 后就可以设计 dp 状态了,即 \(dp_i\) 表示前 \(i\) 组人和马内部完全匹配的最大答案,\(dp_i\) 只能从 \(dp_{i-3},dp_{i-2},dp_{i-1}\) 转移来,于是就可以列出转移矩阵动态 dp 了。
Code
#include<bits/stdc++.h>
#define LL long long
#define inf 0x3f3f3f3f3f3f3f3f
using namespace std;
int n,q;
int idw[30002],idh[30002],tow[30002],toh[30002];
LL w[30002],h[30002],t[30002];
struct Matrix
{
LL a[3][3];
}M[30002];
inline Matrix Mul(Matrix A,Matrix B)
{
Matrix C;
for(int i=0;i<3;++i)
for(int j=0;j<3;++j)
{
C.a[i][j]=-inf;
for(int k=0;k<3;++k)C.a[i][j]=max(C.a[i][j],A.a[i][k]+B.a[k][j]);
}
return C;
}
inline int lson(int x)
{
return (x<<1);
}
inline int rson(int x)
{
return ((x<<1)|1);
}
struct SegTree
{
Matrix a[120002];
inline void build(int k,int l,int r)
{
if(l==r)return (void)(a[k]=M[l]);
int mid=((l+r)>>1),ls=lson(k),rs=rson(k);
build(ls,l,mid),build(rs,mid+1,r),a[k]=Mul(a[rs],a[ls]);
}
inline void modify(int k,int l,int r,int x)
{
if(l==r)return (void)(a[k]=M[l]);
int mid=((l+r)>>1),ls=lson(k),rs=rson(k);
if(x<=mid)modify(ls,l,mid,x);
else modify(rs,mid+1,r,x);
a[k]=Mul(a[rs],a[ls]);
}
}S;
inline bool cmp(int x,int y)
{
return t[x]<t[y];
}
inline void upd(int x)
{
M[x]=(Matrix){{idw[x]!=idh[x]? w[x]*h[x]:-inf,x>1? ((idw[x]!=idh[x-1] && idw[x-1]!=idh[x])? w[x]*h[x-1]+w[x-1]*h[x]:-inf):-inf,x>2? max((idw[x]!=idh[x-1] && idw[x-1]!=idh[x-2] && idw[x-2]!=idh[x])? w[x]*h[x-1]+w[x-1]*h[x-2]+w[x-2]*h[x]:-inf,(idw[x-1]!=idh[x] && idw[x-2]!=idh[x-1] && idw[x]!=idh[x-2])? w[x-1]*h[x]+w[x-2]*h[x-1]+w[x]*h[x-2]:-inf):-inf,0,-inf,-inf,-inf,0,-inf}};
}
int main()
{
scanf("%d%d",&n,&q);
for(int i=1;i<=n;++i)scanf("%lld",&w[i]),idw[i]=i,t[i]=w[i];
sort(idw+1,idw+n+1,cmp);
for(int i=1;i<=n;++i)w[i]=t[idw[i]];
for(int i=1;i<=n;++i)scanf("%lld",&h[i]),idh[i]=i,t[i]=h[i];
sort(idh+1,idh+n+1,cmp);
for(int i=1;i<=n;++i)h[i]=t[idh[i]];
for(int i=1;i<=n;++i)tow[idw[i]]=toh[idh[i]]=i;
for(int i=1;i<=n;++i)upd(i);
S.build(1,1,n);
for(int x,y;q--;)
{
scanf("%d%d",&x,&y),swap(toh[x],toh[y]),swap(idh[toh[x]],idh[toh[y]]);
for(int i=toh[x];i<=min(toh[x]+2,n);++i)upd(i),S.modify(1,1,n,i);
for(int i=toh[y];i<=min(toh[y]+2,n);++i)upd(i),S.modify(1,1,n,i);
printf("%lld\n",S.a[1].a[0][0]);
}
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号