做题笔记

2023.05.08 CF1824B2 LuoTianyi and the Floating Islands (Hard Version)

结论：\(\sum_{j=w+1}^{k}\binom{x}{j}\binom{n-x}{k-j}=\sum_{i=1}^x\binom{i-1}{w}\binom{n-i}{k-w-1}\)。

证明：考虑组合意义，左式表示在一行 \(n\) 个盒子中放 \(k\) 个球，满足前 \(x\) 个盒子至少有 \(w+1\) 个球的方案数（\(j\) 在枚举前 \(x\) 个盒子中的球数），枚举第 \(w+1\) 个球的位置 \(i\)，便可得到右式。

2023.04.13 P6575 [BalticOI 2017] Friends

结论：\(\sum_{i=0}^{p}\sum_{j=0}^{q}\binom{i+j}{i}\lt4\binom{p+q}{\lfloor\frac{p+q}{2}\rfloor}\)。

证明：\(\sum_{i=0}^{p}\sum_{j=0}^{q}\binom{i+j}{i}=\binom{p+q+2}{p+1}-1\lt\binom{p+q+2}{\lfloor\frac{p+q}{2}\rfloor+1}\lt4\binom{p+q}{\lfloor\frac{p+q}{2}\rfloor}\)。

2023.03.28 CF1179D Fedor Runs for President

结论（不会证）：对于一棵 \(n\) 个点的树，记 \(a_i\) 表示点 \(i\) 的儿子中，不同子树大小个数，则 \(\sum_{i=1}^n a_i^2\) 是 \(O(n\log\log n)\) 级别的。

2023.03.25 P3770 [CTSC2017]密钥

定义密钥是一个长度为 \(2k + 1\) 的字符串，它包含 \(1\) 个字母 \(X\)、\(k\) 个字母 \(A\) 和 \(k\) 个字母 \(B\)。按顺时针顺序把这 \(2k+1\) 个字母排成一个圈。从 \(X\) 出发顺时针走到某个 \(A\) 时，如果途中 \(A\) 的数目严格多于 \(B\) 的数目，则称此字母 \(A\) 为「强的」。定义一个密钥的「特征值」是其中包含的「强的」字母 \(A\) 的个数。假设 \(k\) 个字母 \(A\) 所在的位置已经固定，但是剩下的 \(k\) 个 \(B\) 和 \(1\) 个 \(X\) 的位置是未知的。

结论 \(1\)（不会证）：所有 \(k + 1\) 个可能的密钥的特征值恰好为 \(0, 1, 2, …, k\)。

结论 \(2\)：对于由 \(k\) 个 \(1\) 和 \(k\) 个 \(-1\) 组成的序列，\(k\) 个 \(1\) 中前缀和大于 \(0\) 的个数加上 \(k\) 个 \(-1\) 中前缀和小于 \(0\) 的个数等于 \(k\)。

证明 \(2\)：考虑前缀和从 \(0\) 变成正数再变成 \(0\) 的过程中，\(1\) 的个数和 \(-1\) 的个数是相等的，且这些 \(1\) 的前缀和都大于 \(0\)；同理，前缀和从 \(0\) 变成负数再变成 \(0\) 的过程中，\(1\) 的个数和 \(-1\) 的个数也相等，且这些 \(-1\) 的前缀和都小于 \(0\)。

2023.03.19 ZR#2543. 23省选10连测day9-分割

技巧：给定一个长为 \(n\) 的序列，满足存在一个 \(t\) 使得所有长度不超过 \(t\) 的前缀都是「合法」的，所有长度大于 \(t\) 的前缀都是「不合法」的。每次可以 \(O(len)\) 询问一个长为 \(len\) 的前缀是否合法，要求在 \(O(t\log t)\) 时间内找出最长合法前缀。

做法：首先从小到大依次询问长为 \(2\) 的次幂的前缀是否合法，可以确定出最长合法前缀的长度所在区间 \([2^l,2^{l+1})\)，之后再在该区间内二分，时间复杂度为 \(O(2^ll)\)。由于 \(2^l\le t\lt 2^{l+1}\)，所以 \(O(2^l)=O(t)\)，总时间复杂度即为 \(O(t\log t)\)。

2023.02.09 P4240 毒瘤之神的考验

结论：\(\varphi(ij)=\frac{\varphi(i)\varphi(j)(i,j)}{\varphi((i,j))}\)。

证明：记 \(v_p(x)\) 表示 \(x\) 中质因子 \(p\) 的次幂，\(\varphi(ij)=\prod_{p|ij}\varphi(p^{v_p(i)+v_p(j)})=\prod_{p|ij}p^{v_p(i)+v_p(j)-1}(p-1)=\prod_{p|ij}p^{v_p(i)+v_p(j)-2}(p-1)^2\frac{p}{p-1}= \varphi(i)\varphi(j) \prod_{p\nmid i,p|j}\frac{p-1}{p} \prod_{p\nmid j,p|i}\frac{p-1}{p} \prod_{p|ij}\frac{p}{p-1}=\frac{\varphi(i)\varphi(j)(i,j)}{\varphi((i,j))}\)，得证。

2023.02.09 P3327 [SDOI2015]约数个数和

结论：设 \(d(x)\) 为 \(x\) 的约数个数，则 \(d(ij)=\sum_{a|i}\sum_{b|j}[(a,b)=1]\)。

证明：记 \(v_p(x)\) 表示 \(x\) 中质因子 \(p\) 的次幂，\(d(ij)=\prod_{p|ij}d(p^{v_p(i)+v_p(j)})=\prod_{p|ij}(v_p(i)+v_p(j)+1)=\prod_{p|ij}\sum_{x,p^x|i}\sum_{y,p^y|j}[(p^x,p^y)=1]=\sum_{a|i}\sum_{b|j}[(a,b)=1]\)，得证。

2022.11.07 ZR#2481. 22冲刺day17-冰块

结论 \(1\)：设 \(|A|\le|B|\)，\(A,B\) 皆为回文串，则 \(BA\) 为回文串等价于 \(A\) 为 \(B\) 的循环节。

结论 \(2\)：若回文串 \(A,B\) 均为 \(C\) 的循环节，则 \(\gcd(|A|,|B|)\) 为 \(C\) 的周期。

结论 \(3\)：\(t\) 是回文串 \(s\) 的后缀，\(t\) 是 \(s\) 的 border 当且仅当 \(t\) 是回文串。

结论 \(4\)：\(t\) 是回文串 \(s\) 的 border，则 \(|s|-|t|\) 是 \(s\) 的周期，\(|s|-|t|\) 为 \(s\) 的最小周期，当且仅当 \(t\) 是 \(s\) 的最长回文真后缀。

结论 \(5\)：对于 \(s\) 的任一回文子串 \(p\)，设 \(p\) 的最小循环节为 \(t\)，\(|q|\le|p|\) 且 \(q\) 为 \(s\) 的回文子串且 \(pq\) 也为回文串可知 \(q\) 为 \(t\cdots t\)。

证明：首先 \(q^R\) 为 \(p\) 的前缀，\(q\) 为 \(p\) 的后缀，由结论 \(1\) 知 \(q\) 为 \(p\) 的循环节。由结论 \(2\) 知若 \(q_1,q_2\) 均为 \(p\) 的循环节，则 \(\gcd(q_1,q_2)\) 为 \(p\) 的周期。因此所有满足条件的 \(q\) 的长度均为 \(|t|\) 的倍数，结合 \(t\) 为 \(p\) 的循环节知 \(q\) 为 \(t\cdots t\)。

应用：最小循环节可由结论 \(4\) 在 PAM 上通过最长回文真后缀直接找到。结合结论 \(5\) 可 \(O(|s|)\) 求出给定字符串 \(s\) 有多少对回文子串 \(p,q\) 满足 \(pq\) 也为回文串。

2022.11.04 CF575E Spectator Riots

记 \(\odot ABC\) 为 \(\Delta ABC\) 的外接圆，\(R_{ABC}\) 为 \(\odot ABC\) 的半径。

结论 \(1\)：设有四个点 \(A, B, C, D\)，若 \(C, D\) 在直线 \(AB\) 同侧，\(D \notin ⊙ABC\)，且 \(∠ACB < \frac{π}{2}\)，
则 \(R_{ABC} < R_{ABD}\)。

证明 \(1\)：易知 \(0<\angle ADB<\angle ACB<\frac{\pi}{2}\)，由正弦定理知 \(R_{ABC}=\frac{AB}{2\sin\angle ACB}<\frac{AB}{2\sin\angle ADB}=R_{ABD}\)。

结论 \(2\)：设 \(ABCD\) 是一个凸多边形，\(R_{ABC} ≥ R_{ABD}, R_{ACD}, R_{BCD}\)，则 \(D ∈ ⊙ABC\)。

证明 \(2\)：\(\angle ABC,\angle ACB\) 中必有一者为锐角，不妨设 \(\angle ACB\) 为锐角，则由结论 \(1\) 知若 \(D\notin\odot ABC\)，则 \(R_{ABC}<R_{ABD}\)，矛盾！因此 \(D\in\odot ABC\)。

结论 \(3\)：在一些不共线的点中选三个点，使得所有点都在这三个点的外接圆的圆内或圆上，则这三个点只能是这些点的凸包的顶点。

证明 \(3\)：过圆上任意一点作切线，所有点都在切线的一侧，说明这三个点只能是这些点的凸包的顶点。

结论 \(4\)：在一些不共线且构成的凸包的点中选三个点，使得所有点都在这三个点的外接圆的圆内或圆上，则半径最大的外接圆一定满足条件。

证明 \(4\)：设半径最大的外接圆为 \(\odot ABC\)，考虑任意一点在 \(\Delta ABC\) 外的点 \(D\)，由结论 \(2\) 知 \(D\in\odot ABC\)。

结论 \(5\)：在一些不共线且构成的凸包的点中选三个点，最大化它们的外接圆半径，必有最大的外接圆之一是这些点的凸包上相邻三个顶点产生的。

证明 \(5\)：设在圆上有 \(k\) 个点 \(A_1,\cdots,A_k\)，则至少存在两个下标 \(i,j\) 使得 \(A_iA_{i+1},A_{j}A_{j+1}\) 在凸包上不相邻（令 \(A_{k+1}=A_1\)），那么在 \(\overset{\LARGE\frown}{A_iA_{i+1}},\overset{\LARGE\frown}{A_jA_{j+1}}\) 中必有一段是劣弧，设为 \(\overset{\LARGE\frown}{A_iA_{i+1}}\)。于是在凸包上取一点 \(B\) 使得 \(B\) 在劣弧 \(\overset{\LARGE\frown}{A_iA_{i+1}}\) 对应的圆心角内且 \(\angle A_iBA_{i+1}\) 最小，由正弦定理易知 \(R_{A_iA_{i+1}B}\) 比当前半径更大，得证。

2022.11.03 P1224 [NOI2013] 向量内积

结论：对于任意一张至少有一条边的 \(n\) 个点的无向图，满足如下条件的长度为 \(n\) 的排列 \(p\) 不超过总排列数的一半：
对于任意 \(1\le i\le n\)，\(p_1\sim p_{i-1}\) 中与 \(p_i\) 连边的点数恰为偶数。

证明：对于任意一个满足条件的 \(p\)，找到最小的 \(i\) 使得 \(p_i\) 往前有连边，再找到最大的 \(j<i\) 使得 \(p_i,p_j\) 有连边，交换 \(p_i,p_j\)，记该变换为 \(f(p)\)。对于任意一个在 \(f\) 值域内的 \(p\)，找到最小的 \(i\) 使得 \(p_i\) 往前有连边（\(p_i\) 一定往前连了奇数条边），再找到最小的 \(j>i\) 使得 \(p_i,p_j\) 有连边，交换 \(p_i,p_j\)，记该变换为 \(g(p)\)。事实上 \(g\) 是 \(f\) 的逆变换，即 \(g(f(p))=p\)，又由 \(f(p)\ne p\) 且对任意排列 \(p\ne q\) 有 \(f(p)\ne f(q)\)（否则 \(f(p)=f(q)\Rightarrow g(f(p))=g(f(q))\Rightarrow p=q\)）知每个满足条件的排列都能找到唯一与其对应的不满足条件的排列，故原命题得证。

2022.10.24 ZR#2460. 22冲刺day9-计数

结论（不会证）：设 \(n\) 个点的完全图去掉一条 \(m\) 个点的链得到的图的哈密顿路径数量为 \(f_{n,m}\)，记 \(g_{c,m}=f_{m+c,m}\)，则 \(m\ge5\) 时 \(g_{c,m}=(m+c+1)g_{c,m-1}-(m+3c-2)g_{c,m-2}+(5-m+c)g_{c,m-3}+(m+c-3)g_{c,m-4}\)。

2022.08.29 P2305 [NOI2014] 购票

技巧：对于一棵树，设点 \(i\) 的出栈序为 \(d_i\)，则遍历到 \(i\) 时，对于 \(i\) 的每个祖先 \(f\) 都有出栈序 \([d_i,d_f]\) 对应的已被访问过的点有且仅有 \(i\) 到 \(f\) 这条链上的点。

2022.08.28 P5206 [WC2019] 数树

结论：对于 \(n\) 个点的森林，设其有 \(k\) 个连通分量，第 \(i\) 个连通分量的大小是 \(a_i\)，则包含该森林的树的个数为 \(n^{k-2}\prod_{i=1}^{k}a_i\)。

证明：考虑用 \(\text{Matrix-Tree}\) 定理证明，其基尔霍夫矩阵形式如下：

\[\begin{bmatrix} a_1(n-a_1) & -a_1a_2 & -a_1a_3 & \cdots & -a_1a_k \\ -a_2a_1 & a_2(n-a_2) & -a_2a_3 & \cdots & -a_2a_k \\ -a_3a_1 & -a_3a_2 & a_3(n-a_3) & \cdots & -a_3a_k \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ -a_ka_1 & -a_ka_2 & -a_ka_3 & \cdots & a_k(n-a_k) \\ \end{bmatrix}\]

故包含该森林的树的个数为如下矩阵的行列式：

\[\begin{bmatrix} a_1(n-a_1) & -a_1a_2 & -a_1a_3 & \cdots & -a_1a_{k-1} \\ -a_2a_1 & a_2(n-a_2) & -a_2a_3 & \cdots & -a_2a_{k-1} \\ -a_3a_1 & -a_3a_2 & a_3(n-a_3) & \cdots & -a_3a_{k-1} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ -a_{k-1}a_1 & -a_{k-1}a_2 & -a_{k-1}a_3 & \cdots & a_{k-1}(n-a_{k-1}) \\ \end{bmatrix}\]

将第 \(1\) 行加上第 \(2\sim k-1\) 行得：

\[\begin{bmatrix} a_1a_k & a_2a_k & a_3a_k & \cdots & a_{k-1}a_k \\ -a_2a_1 & a_2(n-a_2) & -a_2a_3 & \cdots & -a_2a_{k-1} \\ -a_3a_1 & -a_3a_2 & a_3(n-a_3) & \cdots & -a_3a_{k-1} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ -a_{k-1}a_1 & -a_{k-1}a_2 & -a_{k-1}a_3 & \cdots & a_{k-1}(n-a_{k-1}) \\ \end{bmatrix}\]

将第 \(2\le i\le k-1\) 行加上第一行乘 \(\frac{a_i}{a_k}\) 得：

\[\begin{bmatrix} a_1a_k & a_2a_k & a_3a_k & \cdots & a_{k-1}a_k \\ 0 & a_2n & 0 & \cdots & 0 \\ 0 & 0 & a_3n & \cdots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & 0 & \cdots & a_{k-1}n \\ \end{bmatrix}\]

故其行列式的值为：\(n^{k-2}\prod_{i=1}^{k}a_i\)，原命题得证。

2022.08.05 CF1019D Large Triangle

结论：将平面上 \(n\) 个三点不共线的点两两间连成的 \(A_n^2\) 条有向线段按斜率排序后，设第 \(i\) 条线段两端点编号为 \(a_i,b_i\)，第 \(x\) 个点与第 \(y\) 条线段组成的三角形的有向面积为 \(S_{x,y}\)，\(p_{x,y}\) 为使得 \(S_{t,y}\) 第 \(x\) 小的 \(t\)（\(S\) 相同按 \(t\) 排序），则 \(\forall i\in[1,A_n^2)\)，\(\{p_i\}\) 与 \(\{p_{i+1}\}\) 相比有且仅有 \(a_i\) 与 \(b_i\) 交换了位置。

证明：对于一条两端点编号为 \(x,y\) 的线段 \(l\)，设 \(l\) 的长度为 \(|l|\)，\(a\) 到 \(l\) 的有向距离为 \(d_{a,l}\)，则 \(S_{\Delta axy}=\frac{|l|d_{a,l}}{2}\)。故若 \(S_{\Delta axy}\le S_{\Delta bxy}\)，则 \(d_{a,l}\le d_{b,l}\)，即 \(d_{a,l}-d_{b,l}\le0\)，而平移 \(l\) 并不影响 \(d_{a,l}-d_{b,l}\) 的值，故将 \(l\) 平移至过 \(b\) 点，此时 \(d_{b,l}=0\)，原条件等价于 \(d_{a,l}\le0\)，而这只和 \(l\) 的斜率和直线 \(ab\) 的斜率的大小关系有关，因此 \(a,b\) 在 \(p\) 中的位置发生交换当且仅当 \(l\) 的斜率和直线 \(ab\) 的斜率的大小关系发生改变，原命题得证。

2022.07.11 「2022-07-11 NOI 模拟赛」Graph (graph)

结论：一个 \(n\times n\) 的布尔矩阵（乘法为与，加法为或）的幂的非循环节长度不超过 \(n^2\)。

证明：若布尔矩阵 \(A\) 的 \(A_{i,j}=1\)，则从 \(i\) 向 \(j\) 连一条有向边，\(A^k_{i,j}\) 表示 \(i\) 走 \(k\) 步能否到达 \(j\)。于是非循环节长度即为每个弱连通分量转成矩阵后的幂的非循环节长度取 \(\min\)。由于一个弱连通分量转成矩阵后的幂的循环节长度 \(d\) 是该弱连通分量中所有环长的 \(\gcd\) 不超过弱连通分量的大小，因此可以用 \(d\) 种颜色（\(0\sim d-1\)）染色，满足若 \(x\) 向 \(y\) 连了一条有向边，则 \(col_y=(col_x+1)\bmod d\)。一种颜色的点走 \(d\) 步后只会到达同种颜色的点，于是相当于在一个 \(d^2\) 个点的图上跑同余最短路，答案自然不超过 \(n^2\)。

2022.05.12 CF487E Tourists

结论：点双中任意两点间简单路径经过的点的并集等于该点双中的点。

证明：只需证明点双中任意三点 \(u,v,w\)，一定存在一条 \(u\) 到 \(v\) 的简单路径经过 \(w\)。

首先 \(u\) 到 \(v\) 的简单路径不可能经过点双外的点，否则该点双不为极大点双。

考虑建立网络流模型。源点向 \(w\) 连容量为 \(2\) 的边，对于点双中任意一条边 \((x,y)\)，在新图中分别连 \(x\) 向 \(y\)、\(y\) 向 \(x\) 容量为 \(1\) 的边，\(u,v\) 分别向汇点连容量为 \(1\) 的边，对于点双中的任意一个点，通过拆点将其容量设为 \(1\)。现在等价于证明该图的最大流为 \(2\)。

考虑最大流最小割定理。下面证明任意割掉一条容量为 \(1\) 的边后源点与汇点仍然连通。

1. 删除拆点的边。由点双的定义知剩下任意两点间均可互相到达。故源点与汇点连通。

2. 删除点双中或 \(u,v\) 向汇点连的边。这显然弱于删除拆点的边。故源点与汇点连通。

综上所述，该图最大流为 \(2\)。故原结论成立。

推论：点双中任意两点间简单路径经过的边的并集等于该点双中的边。

证明：首先 \(u\) 到 \(v\) 的简单路径还是不可能经过点双外的边。两点一边的特殊情况是满足条件的，其它情况下点双一定是边双，在每条边 \((u,v)\) 中间建个虚点 \(x\)，删去 \((u,v)\)，连上 \((u,x),(x,v)\)，得到的新图仍然是点双，对该点双用上述结论即可证明。

2022.03.31 P8212 [THUPC2022 初赛] 喵喵花園

结论：若平面上 \(a_1,a_2,\cdots,a_n\) 共 \(n\) 个点依次构成了一个凸多边形，其中 \(|a_2a_3|,\cdots,|a_{n-2}a_{n-1}|\) 和 \(|a_1a_2|+|a_{n-1}a_n|\) 均为定值，且 \(a_1a_2,a_2a_3,\cdots,a_{n-1}a_n\) 的斜率固定，则该凸多边形面积是关于 \(|a_1a_2|\) 上凸的。

证明：首先由 \(S_{\Delta}=\frac{1}{2}ab\sin C\) 知若一个三角形顶角固定且两腰之和为定值，则该三角形面积是关于任意一边的二次项系数为负的二次函数，是上凸的。

接下来的证明中均假设 \(AB+DE\) 为定值。

情况 \(1\)：

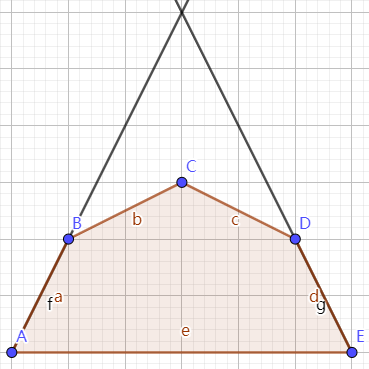
凸多边形面积即为一个满足上述条件的三角形的面积减去一定值，是上凸的。

情况 \(2\)：

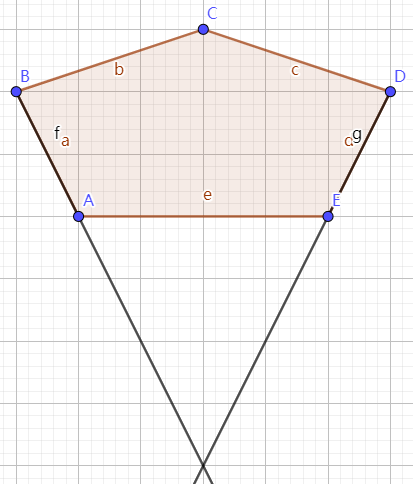
凸多边形面积即为一定值减去一个满足上述条件的三角形的面积，是上凸的。

情况 \(3\)：

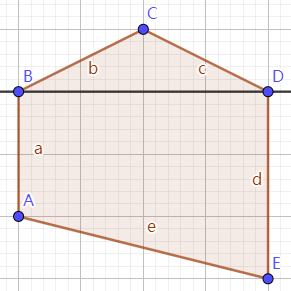
凸多边形面积即为一定值加上一梯形面积，是恒定的。

故原命题得证。

2022.03.31 UVA10228 A Star not a Tree?

结论：对于任意一条直线和任意 \(n\) 个点，都有直线上的点到这 \(n\) 个点的距离和是下凸的。

证明：分别考虑 \(n\) 个点。对于任意一个点，考虑该点与直线构成的平面，则点到线的距离是一个最高项系数为正的二次函数或下凸的分段一次函数。将这 \(n\) 个函数相加，得到的还是一个下凸的函数。得证。

2022.03.26 P7468 [NOI Online 2021 提高组] 愤怒的小 N

结论：对于任意正整数 \(n\)，将 \(0\sim2^n-1\) 按照二进制 \(1\) 的个数的奇偶性分成 \(2\) 组，则有 \(\forall i\in[0,n-1]\)，这两组数的 \(i\) 次方和都相等。

证明：令 \(f_{a,b}=\sum_{i=0}^{2^a-1}(-1)^{pop(i)}i^b\)，其中 \(pop(x)\) 为 \(x\) 二进制表示中 \(1\) 的个数。

由 \(\sum_{i=0}^{2^{a+1}-1}(-1)^{pop(i)}i^b\)

\(=\sum_{i=0}^{2^a-1}(-1)^{pop(i)}i^b-\sum_{i=0}^{2^a-1}(-1)^{pop(i)}(i+2^a)^b\)

\(=\sum_{i=0}^{2^a-1}(-1)^{pop(i)}i^b-\sum_{i=0}^{2^a-1}(-1)^{pop(i)}\sum_{j=0}^{b}C_b^ji^j2^{a(b-j)}\)

\(=\sum_{i=0}^{2^a-1}(-1)^{pop(i)}i^b-\sum_{j=0}^{b}C_b^j2^{a(b-j)}\sum_{i=0}^{2^a-1}(-1)^{pop(i)}i^j\)

知 \(f_{a+1,b}=f_{a,b}-\sum_{j=0}^{b}C_b^j2^{a(b-j)}f_{a,j}\)。

只需证明 \(a\gt b\) 时有 \(f_{a,b}=0\) 即可。

对 \(a\) 进行归纳证明：当 \(a=1\) 时显然成立。若 \(\le a\) 时都成立，则 \(a+1\) 时：

1. \(a\gt b\)：\(f_{a+1,b}=f_{a,b}-\sum_{j=0}^{b}C_b^j2^{a(b-j)}f_{a,j}=0-0=0\)。

2. \(a=b\)：\(f_{a+1,b}=f_{a,a}-\sum_{j=0}^{a}C_a^j2^{a(a-j)}f_{a,j}=f_{a,a}-C_a^a2^{a(a-a)}f_{a,a}=0\)。

得证。故原命题成立。

2022.03.24 P4983 忘情

结论：记 \(f_i\) 表示将一个正整数序列划分为 \(i\) 段后每段平方和之和的最小值，则 \(f_i\) 是关于 \(i\) 的下凸函数。

证明：记正整数序列为 \(a\)，考虑数列 \(a_0,a_1,\cdots,a_n,x\)，其中 \(x\) 为正实数。记将此数列分为 \(i\) 段的答案为 \(ans_{i,x}\)，最优方案中最后一段的起始点最小为 \(p_{i,x}\)（即最小决策点）。由于 \(ans_{i,x}\) 关于 \(x\) 连续，且仅在最优方案中最后一段大小不唯一处不可导，故这样的 \(x\) 值只有有限个。求导得 \(ans^{'}_{i,x}=2(x+sum_n-sum_{p_{i,x}})\)。由于 \(p_{i,x}\le p_{i+1,x}\)，所以 \(ans^{'}_{i,x}\ge ans^{'}_{i+1,x}\)，所以 \(ans_{i,x}-ans_{i+1,x}\) 随 \(x\) 增大不降。由于 \(\lim_{x\to0}(ans_{i,x}-ans_{i+1,x})=f_{i}-f_{i+1}\)，\(\lim_{x\to\infty}(ans_{i,x}-ans_{i+1,x})=f_{i-1}-f_{i}\)，所以 \(f_{i-1}-f_{i}\le ans_{i,x}-ans_{i+1,x}\le f_{i}-f_{i+1}\)。

2021.12.23 「2021-12-23 省选模拟赛」背包 (bag)

技巧：\(n\) 个给定点分别向 \(n\) 个左右端点均不减且总覆盖长度为 \(m\) 的区间连边，直接线段树优化建图复杂度为 \(O(m+n\log m)\)，而用如下方法可以做到 \(O(n+m)\)。

1. 在剩余区间中选出左端点最靠左的区间 \(A\)。

2. 在剩余区间中选出所有与 \(A\) 的右端点 \(a\) 有交的区间，设其中有 \(s_i\) 个区间，其中 \(i\) 是已进行的轮数。

3. 以 \(a\) 为界，对于所有 \(2\) 操作中选出的区间的并覆盖的点，若在 \(a\) 左边则向它后继连边，若在 \(a\) 右边则向它前驱连边，给定点向对应区间的两端点连边。

4. 删去上述操作使用过的区间，若仍存在剩余区间，则继续执行 \(1\) 操作直至不存在剩余区间为止。

分析可知每个点在上述操作中最多被区间的并覆盖 \(2\) 次，故总时间复杂度为 \(O(n+\sum{s_i})=O(n+m)\)。

2021.12.16 P5155 [USACO18DEC]Balance Beam P

结论：在长度为 \(n\) 的数轴上的位置 \(x\) 处，每次等概率向左右移动，若到达 \(0\) 或 \(n\) 即停止，则到达 \(0\) 停止的概率为 \(\frac{n-x}{n}\)，到达 \(n\) 停止的概率为 \(\frac{x}{n}\)。

证明：设 \(f_i\) 表示在位置 \(i\) 处，最终到达 \(n\) 停止的概率，则 \(f_0=0,f_n=n,f_{i}=\frac{f_{i-1}+f_{i+1}}{2}\)。由 \(f\) 为等差数列知 \(f_i=\frac{i}{n}\)。得证。

2021.12.08 CF932E Team Work

结论：\(i^n=\sum_{j=0}^{n}C_i^jS_n^jj!\)，其中 \(S_n^j\) 是第二类斯特林数，即将 \(n\) 个两两不同的元素划分为 \(j\) 个互不区分的非空子集的方案数。

证明：设将 \(n\) 个两两不同的元素，划分到 \(i\) 个两两不同的集合（允许空集）的方案数为 \(G_i\)，将 \(n\) 个两两不同的元素，划分到 \(i\) 个两两不同的非空集合（不允许空集）的方案数为 \(F_i\)。

则 \(G_i=i^n,G_i=\sum_{j=0}^iC_i^jF_j,F_i=S_n^ii!\)。代入即证得原式。

2021.12.05 「2021-12-05 联考」成绩/P2797 Facer的魔法/CF626E Simple Skewness

结论：从 \(n\) 个数中选一些数，使得这些数的平均数减中位数最大，则存在最优解选出奇数个数。

证明：假设一种选出偶数个数的最优解选出的数为 \(a_1,\cdots ,a_{2m}\)，记 \(s=\sum_{i=1}^{2m}a_i\)，则最优解答案为 \(\frac{s}{2m}-\frac{a_m+a_{m+1}}{2}\)，且 \(\frac{s}{2m}\ge\frac{a_m+a_{m+1}}{2}\)，即 \(s\ge m(a_m+a_{m+1})\)。若删去 \(a_{m+1}\)，则答案变为 \(\frac{s-a_{m+1}}{2m-1}-a_m\)。

\(2m(2m-1)\left((\frac{s}{2m}-\frac{a_m+a_{m+1}}{2})-(\frac{s-a_{m+1}}{2m-1}-a_m)\right)\)

\(=(2m-1)s-m(2m-1)(a_m+a_{m+1})-2m(s-a_{m+1})+2m(2m-1)a_{m}\)

\(=(2ma_{m+1}-s)+m(2m-1)(a_m-a_{m+1})\)

\(\le2m(m-1)(a_m-a_{m+1})\le0\)

因此 \(\frac{s}{2m}-\frac{a_m+a_{m+1}}{2}\le\frac{s-a_{m+1}}{2m-1}-a_m\)，答案不会更劣，故结论成立。

2021.11.13 P5665 [CSP-S2019] 划分

结论：将长度为 \(n\) 的正整数序列 \(a_i\) 划分成 \(p+1\) 段，使得 \(\sum_{i=1}^{k_1} a_i\le \sum_{i=k_1+1}^{k_2} a_i \le \dots \le \sum_{i=k_p+1}^n a_i\) 且 \(\left(\sum_{i=1}^{k_1} a_i \right)^2+\left(\sum_{i=k_1}^{k_2} a_i \right)^2+\cdots +\left(\sum_{i=k_p+1}^n a_i \right)^2\) 最小，则划分出的最后一段的和一定最小。

证明：\(n=1\) 时显然。

若 \(n\lt k\) 时都成立，则 \(n=k\) 时：

引理：如果两个划分出来的区间 \([l_1,r_1],[l_2,r_2]\) 满足 \(r_1\le r_2\lt k\)，那么 \(l_1\le l_2\)。

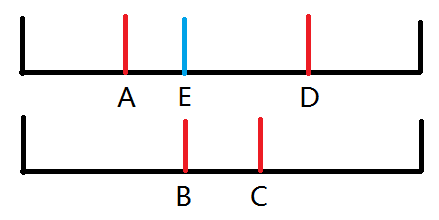
反证：设上图中 \(A=l_2,E=B=l_1,C=r_1,D=r_2\) 满足条件，则由归纳假设知 \(D\) 前最后一段的和越小越好，又因为 \(E=B\)，\(B\) 前存在合法方案，且 \(B\) 前合法方案最后一段的和 \(S\le\sum_{i=B}^{C} a_i\le\sum_{i=E}^{D} a_i\)，故将 \(AD\) 拆成 \(ED\) 和 \(E\) 前的部分更优。矛盾！

于是最终一定是下面两种情况之一（其中第一条红线为两种划分的最后一个公共划分点）：

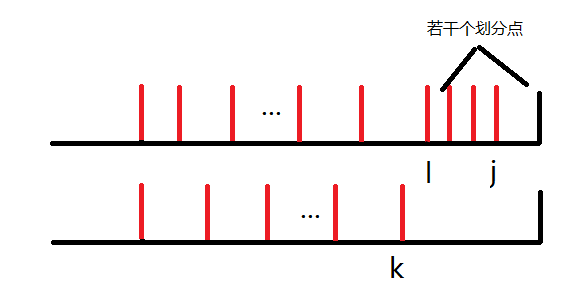
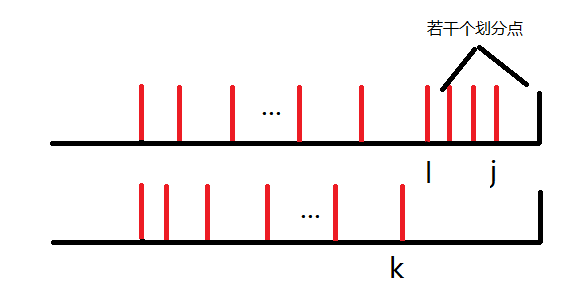
两种情况的区别仅在于公共划分点之后的第一个划分点属于前一种划分还是后一种划分。除了第一种划分中最后的若干个划分点，其它划分点都满足交替出现。

首先 \(j\) 比 \(l\) 优，接下来证明 \(l\) 比 \(k\) 优，故只需考虑如下两种情况。

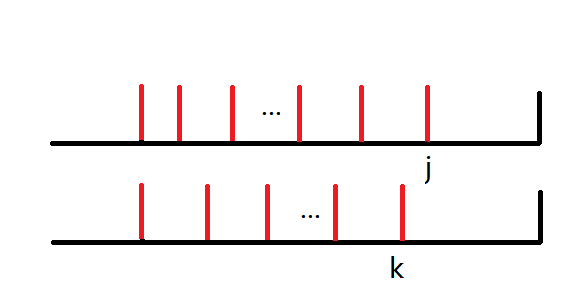
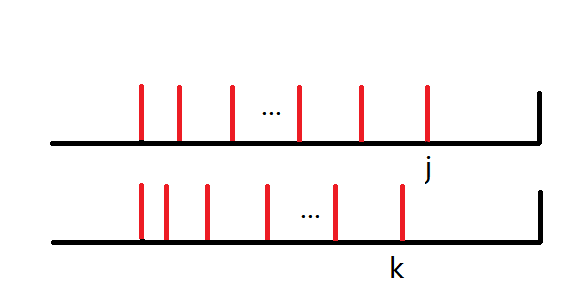
对于一种划分，我们从后往前将每一段划分点间的数字和写出，再在其后补无限个零。

由引理知，满足结论中条件的解对应的序列的任何位置的前缀和一定是所有解对应位置的前缀和中最小的。

现在，我们抛弃原序列，只考虑这个和构成的序列。假设满足结论中条件的解对应的序列是 \(a_i\)，我们现在找到另外一个解，它的序列是 \(b_i\)，显然有 \(\forall k,\sum_{i\le k}b_i\le\sum_{i\le k}c_i\)。

只需证明：\(\sum b^2_i\le\sum c^2_i\)。

注意到对于一个单调不增的序列 \(x\)，如果选出两个下标 \(i\lt j\)，且 \(x_i\ge x_j+2\)，并将 \(x_i\) 减一，\(x_j\) 加一，则操作后 \(x\) 依然单调不增，且该操作会使 \(\sum x_i^2\) 减少。

因此只需证明，可以通过一些合法的移动将 \(b\) 变为 \(a\)，且任意时刻 \(b\) 所有位置的前缀和不小于 \(a\) 对应位置的前缀和，这样就可以证明 \(\sum b_i^2\) 一定不小于 \(\sum a_i^2\)。

令 \(c_i=b_i-a_i\)，\(c\) 的任一前缀和都非负且 \(c\) 内元素总和为 \(0\)。每次取最靠前的正数 \(c_i\) 和最靠前的负数 \(c_j\)，则 \(i<j\) 且 \(b_i\gt a_i\ge a_j\gt b_j\)，即 \(b_i\ge b_j+2\)。将 \(b_i\) 减一，\(b_j\) 加一，容易发现这是一个合法的移动，且保持了前缀和的性质。

于是任何一个解对应的序列都可以通过若干次移动得到满足结论中条件的解对应的解，故满足结论中条件的解的平方和是最小的，是最优解。

2021.11.06 CF975E Hag's Khashba

结论：向量 \((x,y)\) 绕原点旋转 \(\theta\) 角度得到的向量为 \((x\cos\theta-y\sin\theta,x\sin\theta+y\cos\theta)\)。

证明：令复数 \(z_1=x+yi,z_2=\cos\theta+\sin\theta i\)，则 \(z_2\) 的模长为 \(1\)，复角为 \(\theta\)。由「复数相乘，模长相乘，复角相加」知 \(z_1\times z_2\) 在复平面上代表向量 \((x,y)\) 绕原点旋转 \(\theta\) 度得到的向量，即 \((x\cos\theta-y\sin\theta,x\sin\theta+y\cos\theta)\)。得证。

2021.11.06 CF1091E New Year and the Acquaintance Estimation

度数序列：设无向图 \(n\) 个点度数从大到小分别为 \(d_1\sim d_n\)，\(S=(d_1,d_2,\cdots,d_n)\) 为该无向图的度数序列。

称序列 \(S\) 可简单图化当且仅当存在一个简单无向图，其度数序列恰为 \(S\)。

问题：给定一个非负整数组成的度数序列 \(S\)（\(S\) 中数字和为偶数），判断改序列是否可简单图化。

Havel–Hakimi 算法：\(S\) 可简单图化当且仅当 \(S’=(d_2-1,d_3-1,...,d_{d_1+1}-1,d_{d_1+2},...,d_n)\) 只含有非负整数且是可简单图化的。

时间复杂度 \(O(n^2)\)。

Erdős–Gallai 定理：\(S\) 可简单图化当且仅当对 \(\forall k\in[1,n]\)，有 \(\sum_{i=1}^k d_i\le k(k-1)+\sum_{i=k+1}^n \min(d_i,k)\)。

证明：对前 \(k\) 个点分配度数，除了两两间能连 \(C_k^2\) 条边外，剩下的度数还可由后面点的度数补。

由于 \(d_i\) 不增，故可从小到大枚举 \(k\)，维护 \(d_i\) 后缀与 \(k\) 取 \(\min\) 的和（维护第一个 \(\min(d_i,k)=d_i\) 的位置 \(i\)）。

时间复杂度 \(O(n)\)。

2021.11.04 P5416 [CTSC2016]时空旅行

结论：斜率优化中每个凸包的并的答案等于每个凸包的答案的最小/大值。

2021.11.01 CF1516E Baby Ehab Plays with Permutations

结论 \(1\)：一个排列中的任意两个元素交换，该排列的奇偶性发生改变。注：排列的奇偶性即排列逆序数的奇偶性。

证明 \(1\)：首先交换相邻的元素改变排列的奇偶性。

假设交换的两个元素分别为 \(a_x,a_y\)，且 \(x<y\)，则将原排列中 \(a_x\) 移到 \(a_y\) 后改变了 \(y-x\) 次奇偶性，再将 \(a_y\) 移到 \(a_x\) 原来的位置上后改变了 \(y-x-1\) 次奇偶性，新得到的排列与直接交换 \(a_x,a_y\) 两元素得到的排列相同，且新得到的排列的奇偶性相较于原排列发生了改变。所以该结论成立。

结论 \(2\)：一个排列通过交换任意两个元素变成标准排列的次数的奇偶性与该排列的奇偶性相同。

证明 \(2\)：标准排列是偶排列。故由结论 \(1\) 知该结论显然成立。

结论 \(3\)：在全部的 \(n(n\ge2)\) 阶排列中，奇偶排列各占一半。

证明 \(3\)：将排列 \(P\) 与交换排列 \(P\) 的前两个元素得到的排列 \(Q\) 两两配对，排列 \(P,Q\) 奇偶性互异且所有排列都唯一对应一个不同于本身的排列，因此奇偶排列各占一半。

2021.11.01 CF1603C Extreme Extension

结论：对于 \(1\le x\le C\)，\(x,C\in\mathbb{N}\)，\(\lfloor\frac{C}{x}\rfloor\) 最多有 \(O(\sqrt C)\) 种取值。

技巧：若一个数等于定值 \(x\) 除以变量 \(y\)，且 \(y\) 取值变化单调，则暴力更新 \(x\) 的均摊复杂度是 \(O(\sqrt x)\) 的。

2021.10.14 「2021-10-14 提高模拟赛」迷宫 (maze)

结论：如下树形 dp 的时间复杂度看上去是 \(O(n\times maxdep^2)\)，实则为 \(O(n\times maxdep)\)，其中 \(n\) 是点数，\(maxdep\) 是最大深度。

inline void dfs(int x,int f)
{
	siz[x]=1;
	for(i=la[x],v;i;i=edge[i].nx)
		if((v=edge[i].to)!=f)
		{
			dfs(v,x);
			for(j=siz[x];~j;--j)g[j]=f[x][j];
			for(j=siz[x]+siz[v];j>siz[x];--j)f[x][j]=inf;
			for(j=0;j<=siz[x];++j)for(k=0;k<=siz[v];++k)f[x][j+k]=min(f[x][j+k],g[j]+f[v][k]+2);
			siz[x]+=siz[v];
		}
}

证明：由于每个已被 dp 过的子树中深度相同的点都被合并到了一起，所以两个子树合并可以看成两条链合并。

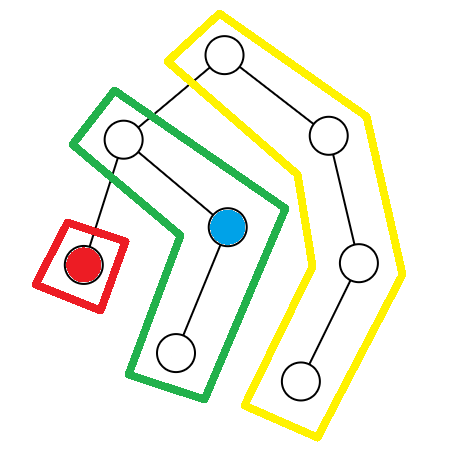
例如上图中红链与绿链合并时，红点被合并到蓝点上了，当再把红绿链组成的子树与黄链合并时，红点和蓝点会同时和黄链形成贡献，所以可看作红点被删去了。

故当较短的链合并到较长的链上时，可看作短的链被删去了，因为它其中的每一个点都被合并到了一个与其深度相同的点上了。

因此考虑总贡献次数，每个点都会在被删去前与它合并到的链上的每个点花费 \(O(1)\) 时间产生贡献，总共 \(n\) 个点，当次贡献复杂度为 \(O(maxdep)\)，所以总复杂度就是 \(O(n\times maxdep)\)。

2021.10.05 CF1580B Mathematics Curriculum

结论：若序列 \(a\) 中元素互不相同，则 \(a\) 中包含 \(a_x\) 的所有子段的不同最大值个数为 \(a_x\) 在该序列对应的大根笛卡尔树上的深度。

证明：对排列长度 \(n\) 进行归纳证明。

\(n=1\) 时，显然成立。

若 \(n\le k\) 时都成立，则 \(n=k+1\) 时：

找出该序列最大值所在位置 \(x\)，则 \(a_x\) 左右两端的区间（如果存在） \([1,x-1]\) 和 \([x+1,k+1]\) 的长度都不超过 \(k\)，且可建出对应的两棵大小分别为 \(x-1\) 和 \(k+1-x\) 的大根笛卡尔树，由归纳假设知两边的区间分别满足条件且互不相干。加入 \(a_x\) 后，向左右两棵笛卡尔树的根节点连边，得到原区间对应的笛卡尔树，此时所有元素的深度都增加 \(1\)，且对于任意一个元素，包含它的所有子段的不同最大值都多了一个 \(a_x\)。

故原结论成立。

2021.08.23 BZOJ3568 DZY Loves Math VII

结论：\(\sum_{i=2}^{n}\sum_{j|i\&j<i}\mu(j)=\sum_{i=2}^{n}\sum_{j=1}^{\lfloor\frac{n}{i}\rfloor}\mu(j)\)。

证明：考虑每个 \(\mu(k)\) 对左右两式的贡献。

在左式中，\(\mu(k)\) 在 \(k\) 是 \(i\) 的真因子时才有贡献，也就是出现次数为 \(\lfloor\frac{n}{k}\rfloor-1\)。

在右式中，\(\mu(k)\) 有贡献当且仅当 \(k\le\lfloor\frac{n}{i}\rfloor\)，也就是说贡献次数 \((i-1)\) 满足 \(k\le\lfloor\frac{n}{i}\rfloor\) 且 \(k\gt\lfloor\frac{n}{i+1}\rfloor\)，移项得 \(\frac{n}{k}-1\lt i\le\frac{n}{k}\)，也就是说 \(i=\lfloor\frac{n}{k}\rfloor\)。

所以每个 \(\mu(k)\) 对左右两式的贡献相等，原式得证。

2021.04.08 P4151 [WC2011]最大XOR和路径

结论：在异或意义下，对一个连通图 dfs 一遍得到的环，可以构成该连通图的所有环。

证明：dfs 一次后会形成一棵 dfs 树，所有且仅有只包含一条非树边的环会被找到，而其他的环至少有两条非树边，故它们都可以通过只包含一条非树边的环异或得到。

2021.03.30 P6186 [NOI Online #1 提高组] 冒泡排序

结论：在 \(n\) 个数的排列 \(\{a_i\}\) 中，设 \(a_i\) 前比它大的数有 \(c_i\) 个，则每经过一轮冒泡排序，\(c_i=\max(c_i-1,0)\)。

证明：假设经过一轮冒泡排序后，\(c_i\) 变为了 \(c_i-k_i\)，显然 \(0 \leq k_i \leq 1\)。

考虑什么时候 \(k_i=0\)。

• 若 \(a_i\) 前没有比它大的数，此时 \(c_i=0\)，\(k_i=0\)。

• 否则设 \(a_i\) 前第一个比它大的数为 \(a_j\)，则在判断 \(a_{j-1}\) 和 \(a_j\) 的大小时，\(a_j\) 要么保持不变，要么变成更大的 \(a_{j-1}\)。无论哪种情况，交换后的 \(a_j\) 一定大于 \([j+1,i]\) 中任意一个数，会被一直交换至少至 \(a_i\)，故此时 \(k_i=1\)。

因此原结论成立。

2021.03.22 OI Wiki-块状数组/P4168 [Violet]蒲公英

技巧：分块数组题可以尝试开两个数组。

设单位操作时间复杂度为 \(O(L)\)，序列长度为 \(n\)，块长为 \(s\)，块数为 \(\dfrac{n}{s}\)。

1. \(s[i][j]\)：第 \(i\) 个块到第 \(j\) 个块的答案。\(O\left(\dfrac{n}{s}\right)\) 枚举左端块，每次 \(O(nL)\) 正扫一遍，时间复杂度 \(O\left(\dfrac{n^2L}{s}\right)\)。

2. \(p[i][j]\)：前 \(i\) 个块 \(j\) 的情况。\(O(nL)\) 正扫一遍，第一维 \(O\left(\dfrac{n}{s}\right)\)，第二维 \(O(n)\)，时间复杂度 \(O\left(\dfrac{n^2L}{s}\right)\)。

一般取 \(s=\sqrt{n}\)，结合题目具体操作，可达到 \(O(n\sqrt{n}L)\) 的时间复杂度。

2021.03.13 OI Wiki-指数生成函数

结论：\(\sum_{n\ge 1}\dfrac{x^n}{n}=-\ln(1-x)\)。

证明：记 \(f^{(n)}(x)\) 表示将 \(f(x)\) 求导 \(n\) 次后的结果。

结论 \(1\)：令 \(f(x)=-\ln(1-x)\)，则 \(f^{(n)}(x)=\dfrac{(n-1)!}{(1-x)^{n}}\)

证明 \(1\)：\(n=1\) 时显然相等。

假设 \(n-1\) 时相等，则 \(n\) 时：

\(LHS=\left(f^{(n-1)}(x)\right)'\)

\(=\left(\dfrac{(n-2)!}{(1-x)^{n-1}}\right)'\)

\(=(n-2)!\left(\dfrac{1}{(1-x)^{n-1}}\right)'\)

\(=(n-2)!(-1)\dfrac{1}{\left((1-x)^{n-1}\right)^2}((1-x)^{n-1})'\)

\(=(n-2)!(-1)\dfrac{1}{(1-x)^{2n-2}}(n-1)(1-x)^{n-2}(-1)\)

\(=\dfrac{(n-1)!}{(1-x)^{n}}=RHS\)

因此左右两式相等。

回到原题，我们要证 \(\sum_{n\ge 1}\dfrac{x^n}{n}=-\ln(1-x)\)。

令 \(f(x)=-\ln(1-x)\)，将 \(f(x)\) 在 \(x=0\) 处泰勒展开：

\(f(x)=\sum_{n\ge0}\dfrac{{f^{(n)}}(0)}{n!}(x-0)^n\)

\(=\sum_{n\ge0}\dfrac{\dfrac{(n-1)!}{(1-0)^{n}}}{n!}(x-0)^n\)

\(=\sum_{n\ge 1}\dfrac{x^n}{n}=LHS\)

因此原结论中左右两式相等。

2021.03.13 OI Wiki-普通生成函数

请求出下列数列的普通生成函数（形式幂级数形式和封闭形式）。

\(a_n=\binom{m+n}{n}\)（\(m\) 是常数，\(n\ge0\)）。

形式幂级数形式：\(\sum_{n\ge 0}\binom{m+n}{n}x^n\)。

封闭形式：\(\dfrac{1}{(1-x)^{m+1}}\)。

结论 \(1\)：\(C_{m+n}^{n}=C_{m+n-1}^{n}+C_{m+n-1}^{n-1}\)。

证明 \(1\)：杨辉三角基本性质。

结论 \(2\)：\(\sum_{i=0}^{n}C_{m+i-1}^{i}=C_{m+n}^{n}\)（\(m\ge1\)）。

证明 \(2\)：\(n=0\) 时显然相等。

假设 \(n-1\) 时相等，则 \(n\) 时：

\(LHS=\sum_{i=0}^{n}C_{m+i-1}^{i}\)

\(=\sum_{i=0}^{n-1}C_{m+i-1}^{i}+C_{m+n-1}^{n}\)

\(=\sum_{i=0}^{n-1}C_{m+i-1}^{i}+C_{m+n}^{n}-C_{m+n-1}^{n-1}\)

\(=C_{m+n}^{n}=RHS\)

因此左右两式相等。

回到原题，我们要证 \(\sum_{n\ge 0}\binom{m+n}{n}x^n=\dfrac{1}{(1-x)^{m+1}}\)。

\(m=0\) 时显然相等。

假设 \(m-1\) 时相等，则 \(m\) 时：

\(RHS=\dfrac{1}{(1-x)^{m+1}}\)

\(=\dfrac{1}{(1-x)^{m}}\times\dfrac{1}{1-x}\)

\(=\sum_{n\ge 0}\binom{m-1+n}{n}x^n\sum_{n\ge 0}x^n\)

\(=\sum_{n\ge 0}x^n\sum_{i=0}^{n}\binom{m-1+i}{i}\)

\(=\sum_{n\ge 0}x^nC_{m+n}^{n}=LHS\)

因此原数列的普通生成函数的封闭形式为 \(\dfrac{1}{(1-x)^{m+1}}\)。

2021.02.18 P4821 [中山市选]生成树

结论：\(\sum_{i=0}^{n}C_{n}^{i}\times a^{n-i}\times(n-i)=a\times n\times(a+1)^{n-1}\)。

证明：注意到两边都是关于 \(a\) 的 \(n\) 次多项式，我们只需证明它们系数对应相等即可。

考虑 \(a^k(0\le k\le n)\) 在左右两式的系数：

左式：\(C_{n}^{n-k}\times k=\dfrac{n!}{(n-k)!\times k!}\times k=\dfrac{n!}{(n-k)!\times (k-1)!}\)。

右式：\(C_{n-1}^{k-1}\times n=\dfrac{(n-1)!}{(n-k)!\times k!}\times n=\dfrac{n!}{(n-k)!\times (k-1)!}\)。

因此左右两式相等。