第二次作业
学习心得
这门课老师教的很好,掌握了很多东西,有些东西理解的不够纯粹是因为我的数学知识不足,最后一章上的比较急难度也比较大,理解的稍微差了些,有待加强
第一章 模式识别基本概念
1.1什么是模式识别
模式识别是根据已有知识的表达,针对待识别模式,判别其决策所属的类别或者预测其对应的回归值,可分为回归和分类两种形式。
回归:输出量是单个/多个维度连续信号的表达
分类:输出量是离散类型的表达,用于判断物体的类别
联系:回归是分类的基础:离散的类别值是由回归值做判别决策得到的
1.2模式识别数学表达
数学解释:模式识别可以看作一种函数映射f(x),将待识别模式 x 从输入空间映射到输出空间。f(x)可以是确定值或概率值。
输入空间:原始输入数据x所在的空间,维度取决于输入数据的维度
输出空间:输出的类别或回归值所在的空间,可为1维、类别的个数、回归值维度
判别函数:
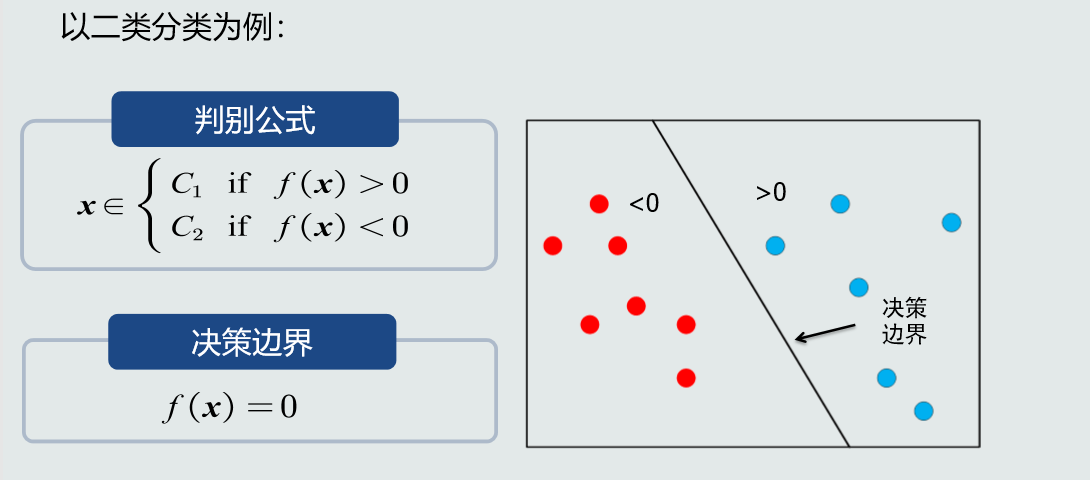
特征向量:

1.3特征向量的相关性
点积:表征两个特征向量的共线性,即方向上的相似程度。
特征向量投影:向量x能够分解到y方向的投影越多,说明两个向量方向上越相似

欧氏距离度量:综合考虑方向和模长

1.4机器学习基本概念
模型的参数和结构:

线性模型:

非线性模型
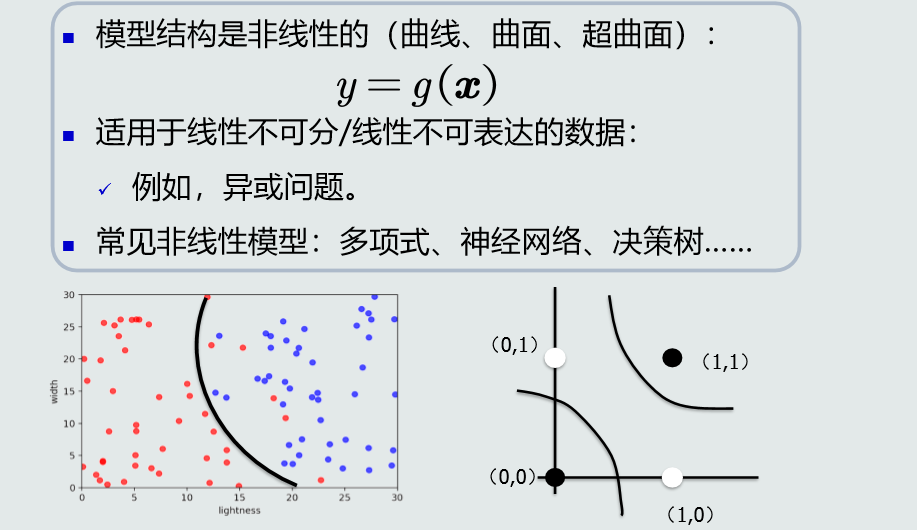
样本量和模型参量

优化算法

监督学习:训练样本及其输出真值都给定情况下的机器学习算法, 通常使用最小化训练误差作为目标函数进行优化。
无监督学习:只给定训练样本、没有给输出真值情况下的机器学习算法,根据训练样本之间的相似程度来进行决策
半监督学习:既有标注的训练样本、又有未标注的训练样本情况下的 学习算法,看做有约束条件的无监督式学习问题:标注过的训练样本用作 约束条件。
1.5模型的泛化能力
训练集:模型训练所用的样本数据。
测试集:测试模型性能所用的样本数据。
误差:模型给出的预测/决策输出与真值之间的差异。
训练误差:模型在训练集上的误差。
测试误差:模型在测试集上的误差。它反映了模型的泛化能力,也称作泛化误差。
过拟合:模型训练阶段表现很好,但是在测试阶段表现很差。
提高泛化能力:
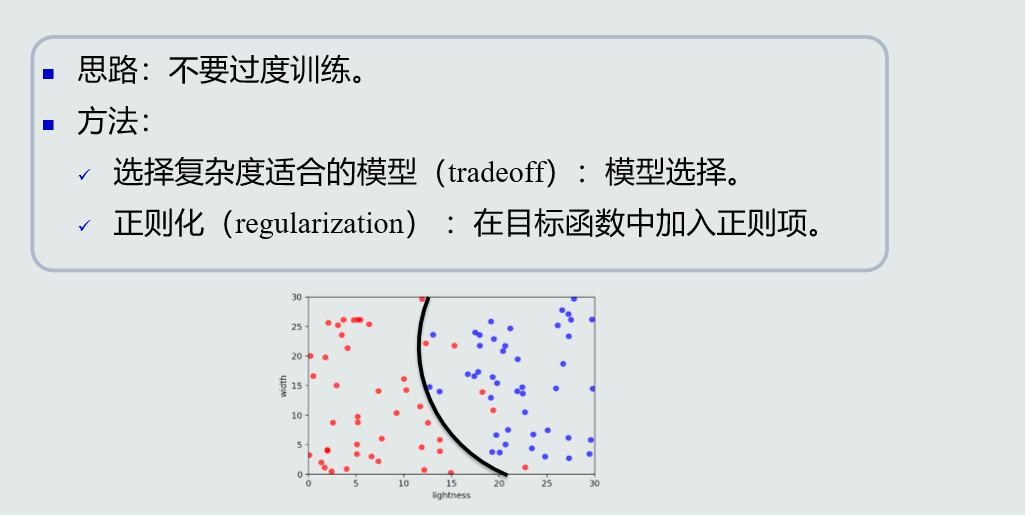
1.6评估方法与性能指标
选取训练集和测试集的方法:
留出法

k折交叉验证

留一验证

评价指标:

第二章 基于距离的分类器
2.1MED分类器
基于距离的分类:
通过测试样本到每个类之间的距离来进行分类
判别公式:
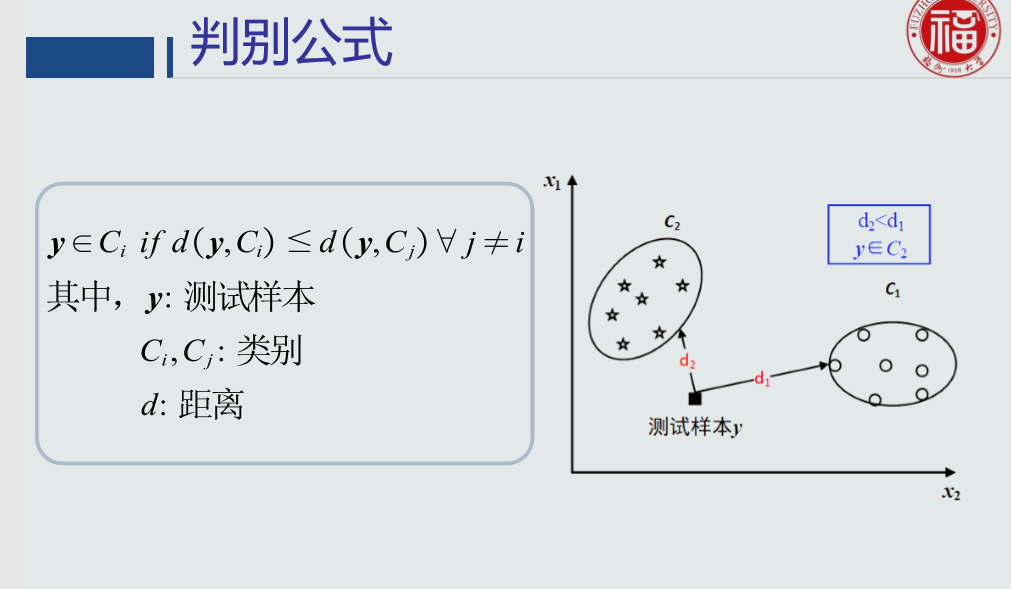
常见距离度量:

MED分类器是基于欧式距离的分类器,决策边界为:

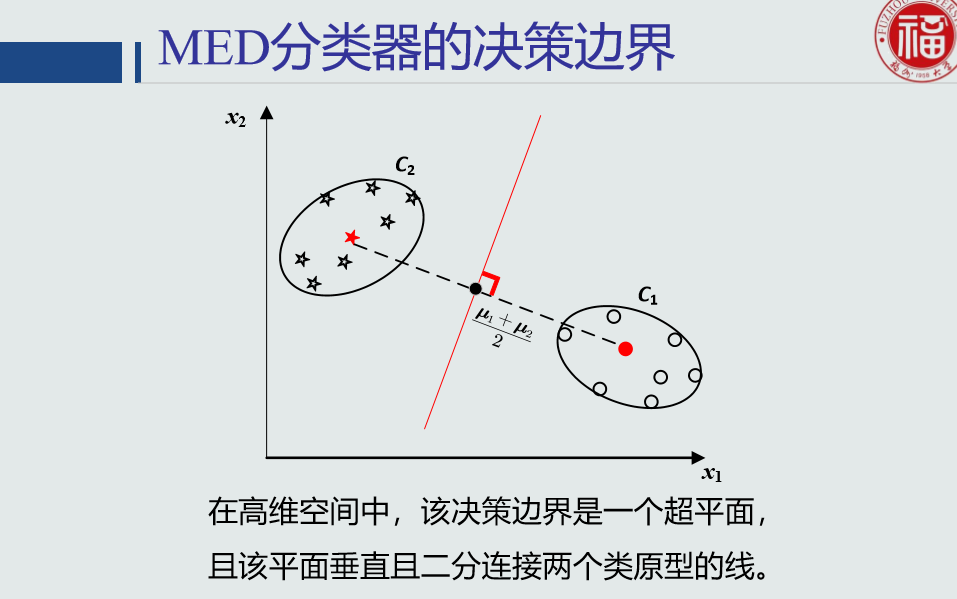
由于没有考虑 特征变化的不同及特征之间的相关性,识别效果不是很好
2.2特征白化
将原始特征映射到一个新的特征空间,使得在新空间 中特征的协方差矩阵为单位矩阵,从而去除特征变化的不同及特征之间的相关性。

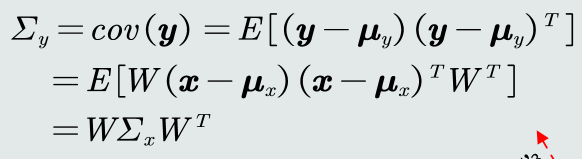

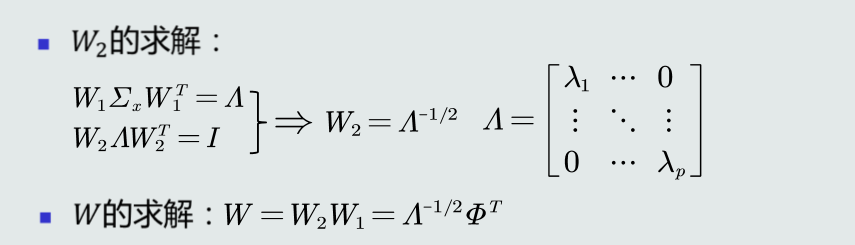
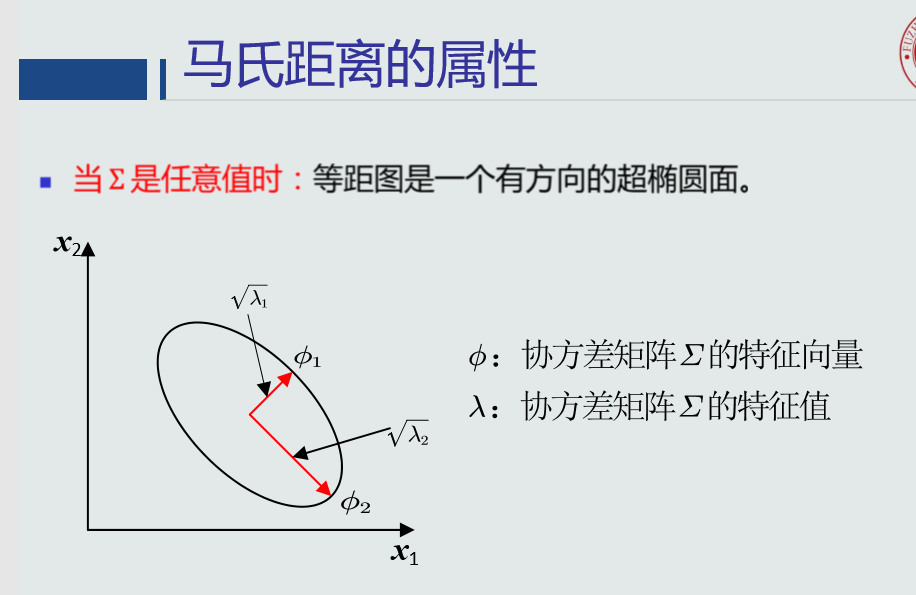
2.3MICD分类器
MICD分类器是一个基于马氏距离的分类器


第三章 贝叶斯决策与学习
3.1贝叶斯决策与map分类器
贝叶斯决策基于后验概率进行决策

map分类器总是选择后验概率最大的那个类

决策误差

3.2高斯观测概率
将观测概率认为符合高斯分布,得到决策边界
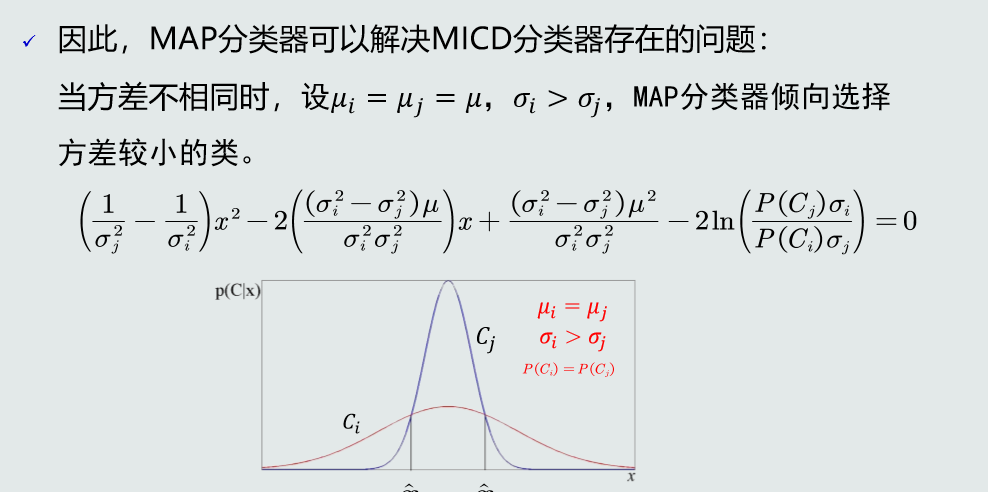
3.3决策风险与贝叶斯分布
贝叶斯分类器选择决策风险最小的类

贝叶斯决策的期望损失为所有样本的决策损失之和

朴素贝叶斯分类器

3.4 3.5 最大似然估计
概率密度函数记为 p(x|θ),θ 是待学习的参数。
求出θ则可以得到概率密度函数

3.6 3.7贝叶斯估计
贝叶斯估计:给定参数θ分布的先验概率以及训练样本,估计参数θ分布的后验概率

3.8KNN估计

3.9直方图与核密度估计
直方图估计


核密度估计

第四章 线性判据与回归
4.1 4.2 线性判据
线性判据:
如果判别模型 f(x) 是线性函数,则 f(x) 是线性判据,计算量少,适用于训练样本较少的情况下。
模型与判别公式:
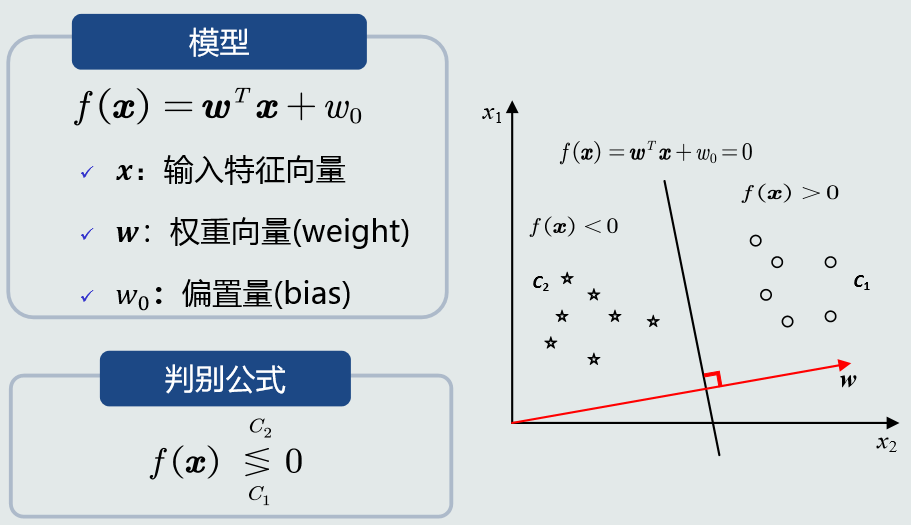
决策边界:

4.3 4.4 感知机算法
并行感知机
预处理:
步骤1:将两个参数合为一个参数 a,线性判据改写为:

步骤2:将C2类的训练样本全部取反:
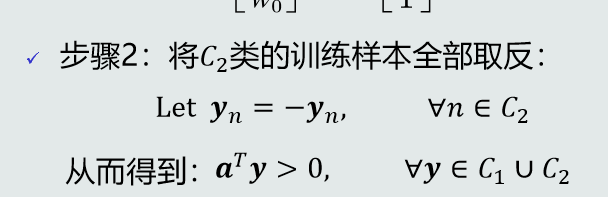
目标函数:针对所有被错误分类的训练样本,其输出值取反求和:

梯度下降法:
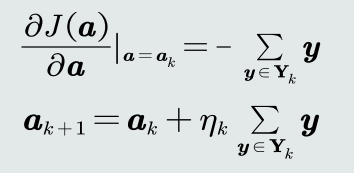
串行感知机
由于是一个一个给出的,所以要不断循环

4.5 Fisher线性判据
基本原理:找到一个最合适的投影轴,使两类样本在该轴上投影的重叠部分最少,从而使分类效果达到最佳。
最佳标准之一:投影后,使得不同类别样本分布的类间差异尽可能大,同时使得各自类内样本分布的离散程度尽可能小。
类间样本的差异程度:用两类样本分布的均值之差度量。
类内样本的离散程度:用每类样本分布的协方差矩阵表征。
目标函数:

作定义:

最优解:

线性判别依据:

决策边界:

4.6支持向量机
设计思想:给定一组训练样本,使得两个类中与决策边界最近的训练样本到决策边界之间的间隔最大。
支持向量的概念:

间隔计算:

目标函数:

4.7 4.8拉格朗日乘数法及对偶问题
拉格朗日函数:

对偶问题:
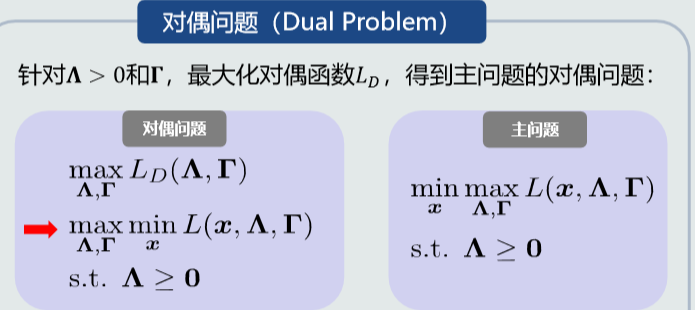
4.9支持向量机学习算法
拉格朗日函数:

对偶函数:

目标函数 L 对 w 和 w0 求导,并设偏导等于0:

目标函数变为:

用二次规划求得:
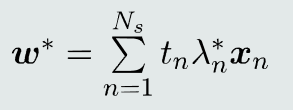
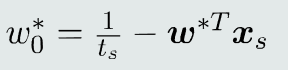
识别决策:



