1.学习总结(2分)
1.1图的思维导图
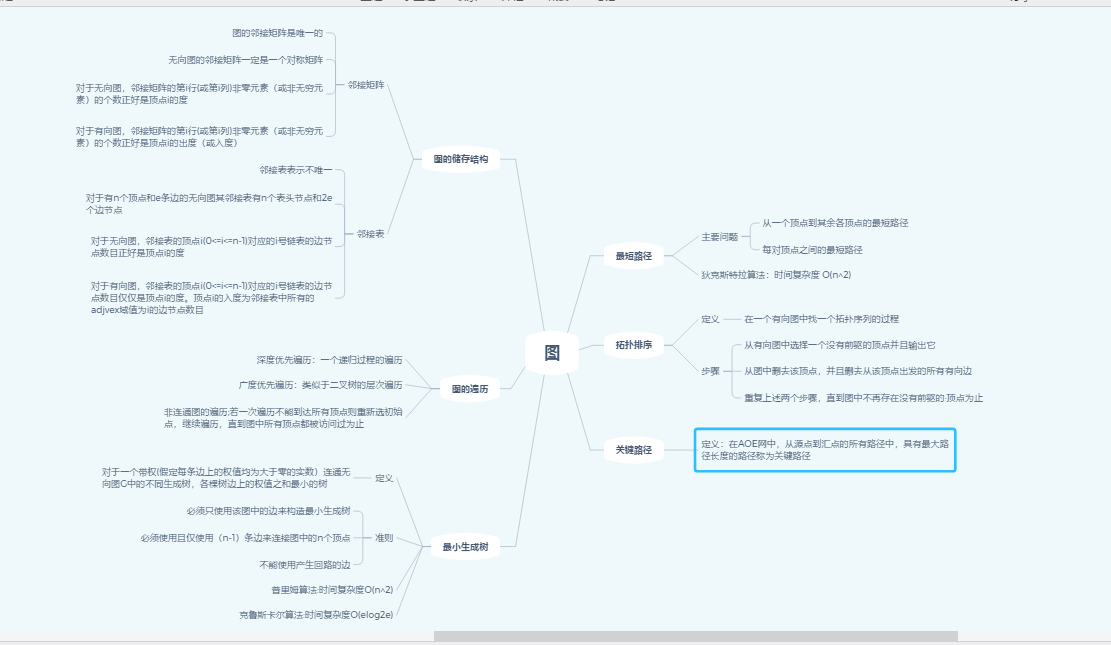
1.2 图结构学习体会
深度遍历算法
广度遍历算法
Prim和Kruscal算法
- 这两种算法都是用来求最小生成树的,Prim适用于邻接矩阵储存和较密的图,Kruscal算法适用于邻接表储存和较稀疏的图
Dijkstra算法
- Dijkstra算法是用来求最短路径的,适用于求邻接矩阵储存,不适用于求权值有负数的图
拓扑排序算法
- 拓扑排序可以用栈也可以用队列,通过在结构体新加一个变量表示入度来实现。
2.PTA实验作业(4分)
2.1 题目1:图着色问题
2.2 设计思路(伪代码或流程图)
输入顶点数a与边数v,颜色数e
置flag的初值为0
建图
深度遍历
输入待检查的颜色分配方案的个数n
while(n-- ){
for j=1 to 顶点数{
输入颜色的分配方案,统计所用颜色总数sum
}
若统计的颜色总数sum!=题干的颜色数
flag=1
}
将颜色按深度遍历
for i=0 to 顶点数{
for j=0 to 顶点数{
若有相邻的颜色相同
flag=1
}
flag=1停止循环
}
如果flag=1 输出no 否则 输出yes
2.3 代码截图(注意,截图、截图、截图。代码不要粘贴博客上。不用用···语法去渲染)
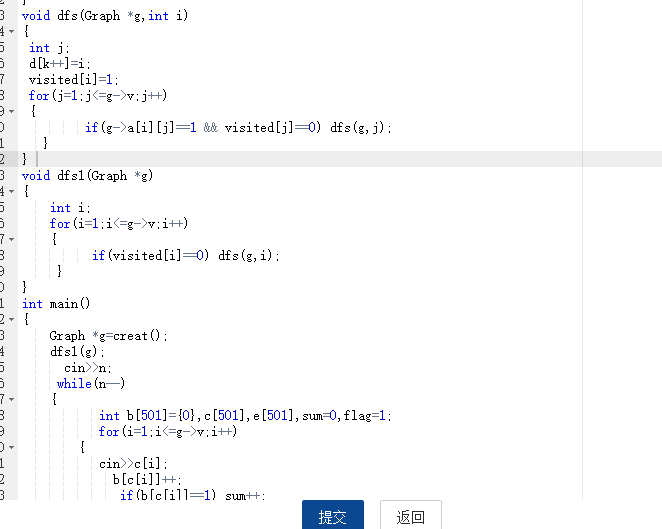
2.4 PTA提交列表说明。

- 一开始创建函数那边忘记申请空间导致段错误

- 第二次因为深度遍历那边的循环变量错了又是段错误
2.1 题目2: 排座位
2.2 设计思路(伪代码或流程图)
定义变量result存放结果,count辅助判断结果
输入M,N,count;
创建图
for 0到count{
输入k1,k2;
如果g.relation[k1][k2]==1
输出"No problem";
else if(g.relation[k1][k2]==-1){
广度遍历找有没有共同的朋友 即 result=BFS(g,k1,k2);
如果(result==0)
输出 "No way";
否则输出 "OK but...";
}
else if(g.relation[k1][k2]==0) 输出"OK";
}
2.3 代码截图(注意,截图、截图、截图。代码不要粘贴博客上。不用用···语法去渲染)
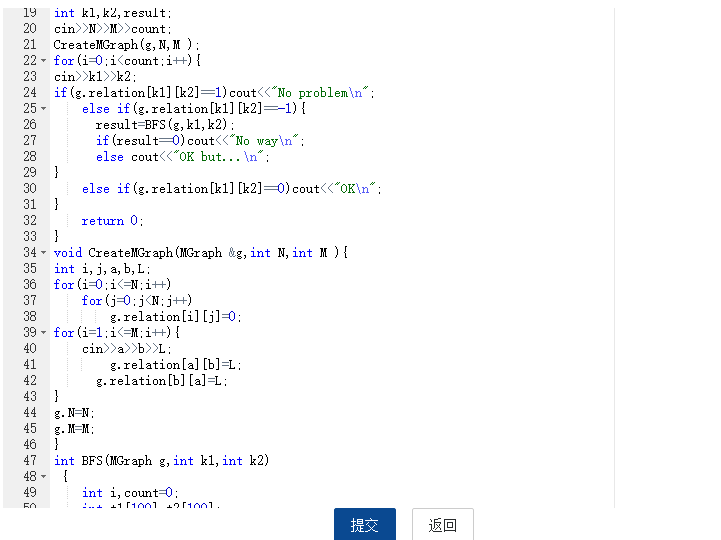
2.4 PTA提交列表说明。

- 最大N的那个测试点过不去
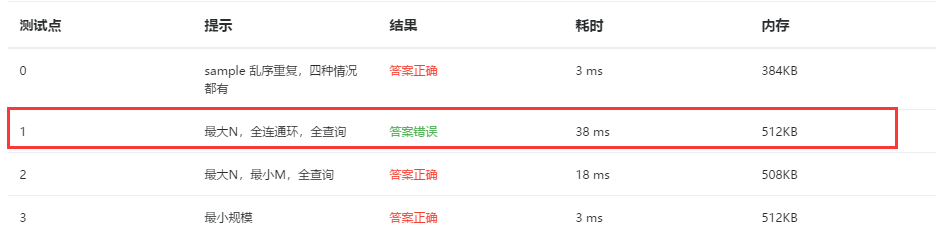
- 一开始我以为是g.relation[k1][k2]的值错了,但是修改这个原本为-1的值以后就会导致所有答案错误,所以我现在也没有找出来问题在哪

2.1 题目3:六度空间
2.2 设计思路(伪代码或流程图)
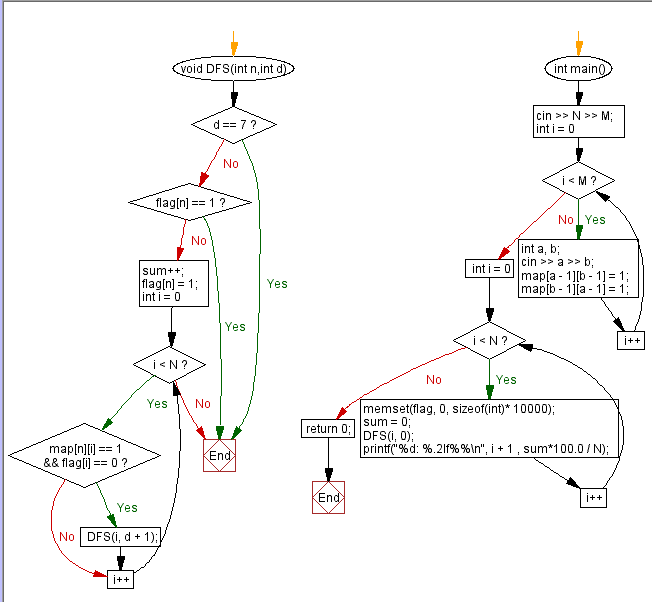
2.3 代码截图(注意,截图、截图、截图。代码不要粘贴博客上。不用用···语法去渲染)
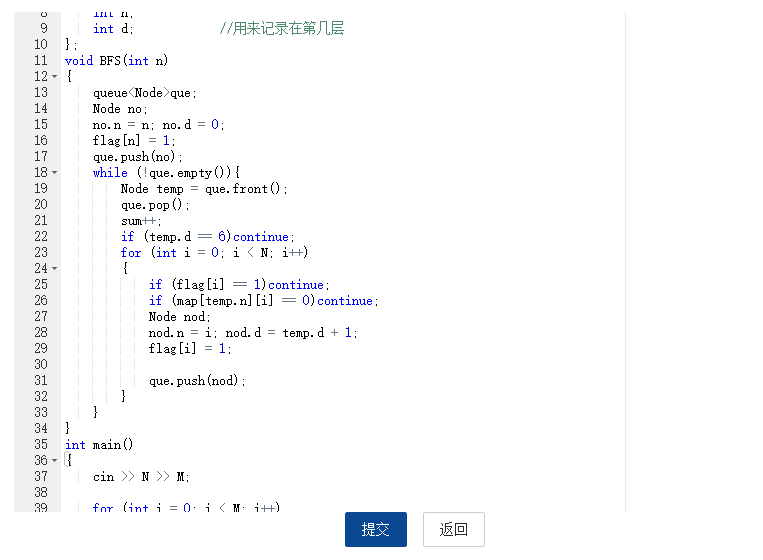
2.4 PTA提交列表说明。
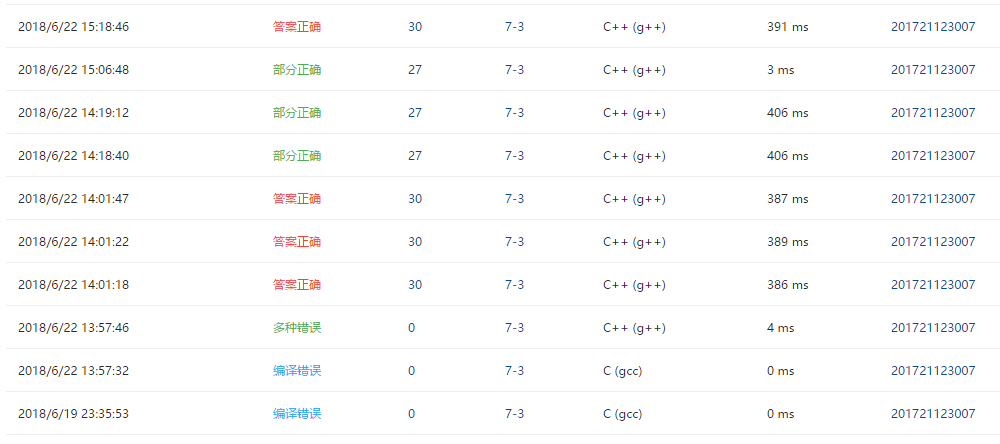
- 一开始用深度遍历,但是最后一个测试点没有正确,我也不知道为什么

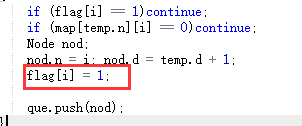
- 后来改用广度遍历,最后一个测试点就运行超时了,大概是因为用了memset函数。后面加上了 flag[i] = 1;将flag置回初值就不会运行超时了
3.截图本周题目集的PTA最后排名(3分)
3.1 PTA排名(截图带自己名字的排名)


3.2 我的总分:192
4. 阅读代码(必做,1分)
pta 7-4题公路村村通,在别人的博客里看到的写法
#include<cstdio>
#include<iostream>
#include<algorithm>
using namespace std;
#define N 1005
int f[N];
/*树的母节点,例如节点1的母节点f[1]=2,那么2就是节点1的母节点*/
struct edge
{
int l,r,dis;
bool friend operator < (edge a,edge b)
/*操作符重载,记得这种sort排序结构体数组的格式,因为没有深入学习*/
{
return a.dis<b.dis;
}
}e[N<<2];
int sanda(int a)
/*sanda=search and adjust——搜索母节点并且调整母节点*/
/*这个函数就是用来告诉你母节点是谁,在那之前,母节点会被调整为最顶层的母节点——节点a的母节点是自己,
即a=f[a]——这个最终的母节点的值相当于不同森林的编号*/
{
if(a==f[a]) return f[a];
/*找到了最终的母节点*/
else
{
f[a]=sanda(f[a]);
/*我的母节点的母节点的母节点的母节点……是我的母节点,在找到原始点后,
最终效果相当于直接把原始点当做自己的直接母节点,当然在那之前,它原来的母节点已经先行完成这一操作了*/
/*不用担心操作在中间进行而导致不能一次性更新完全,反正下一次用到它,
它还是要先完成找到最终的母节点才能进行操作的,而只要它之前有母节点,就能顺藤摸瓜*/
return f[a];
}
}
int main()
{
int n,m,cnt=0,sum=0;
cin>>n>>m;
int i,j,k;
for(i=1;i<=m;i++)
{
cin>>e[i].l>>e[i].r>>e[i].dis;
}
for(i=1;i<=n;i++)
f[i]=i;
sort(e,e+m);
for(i=1;i<=m;i++)
{
if(cnt==n-1) break;
int fa=sanda(e[i].l);
int fb=sanda(e[i].r);
if(fa==fb) continue;
//如果节点fa和fb在同一棵森林里面,就继续
sum+=e[i].dis;
f[fa]=f[fb];
cnt++;
}
if(cnt==n-1) cout<<sum;
else cout<<-1;
return 0;
}
- 这题本来是Prime算法的简单应用,求出最小生成树即可,但是这个做法加了一个sanda函数来搜索母节点并且调整母节点,感觉这样的做法也很巧妙





















