博客作业03--栈和队列

1.学习总结(2分)

1.1 写出你认为本周学习中比较重要的知识点关键词，如逻辑结构、栈、队列、存储结构等。

逻辑结构

逻辑结构大概可以分为两种：线性结构和非线性结构

• 线性结构：有且只有一个开始结点和一个终端结点，并且所有结点都最多只有一个直接前驱和一个直接后继。例如：线性表，典型的线性表有：顺序表、链表、栈（顺序栈、链栈）和队列（顺序队列、链队列）。它们共同的特点就是数据之间的线性关系，除了头结点和尾结点之外，每个结点都有唯一的前驱和唯一的后继，也就是所谓的一对一的关系。
• 非线性结构：对应于线性结构，非线性结构也就是每个结点可以有不止一个直接前驱和直接后继。常见的非线性结构包括：树（二叉树）、图（网）等。

存储结构

储存结构大概也可以分成两种顺序存储、链式存储

• 顺序存储：把逻辑上相邻的节点存储在物理位置上相邻的存储单元中，结点之间的逻辑关系由存储单元的邻接关系来体现。由此得到的存储结构为顺序存储结构，通常顺序存储结构是借助于数组来描述的。优点：节省空间，可以实现随机存取；缺点：插入、删除时需要移动元素，效率低。

• 链式存储：在计算机中用一组任意的存储单元存储线性表的数据元素(这组存储单元可以是连续的,也可以是不连续的)。特点是元素在物理上可以不相邻，所以每个数据元素包括了一个数据域和一个指针域，数据域用来存放数据，而指针域用来指向其后继结点的位置。优点：插入、删除灵活；缺点：不能随机存取，查找速度慢。

栈

• 栈是一种运算受限的线性表。其限制是仅允许在表的一端进行插入和删除运算，对于栈的操作有进栈，出栈，销毁栈，初始化栈与取栈顶元素。栈最需要注意的是栈是后进先出表。

队列

• 队列是一种特殊的线性表，特殊之处在于它只允许在表的前端（front）进行删除操作，而在表的后端（rear）进行插入操作，和栈一样，队列是一种操作受限制的线性表。进行插入操作的端称为队尾，进行删除操作的端称为队头。所以说，队列与现实中的排队很像，都是先进先出。

2.PTA实验作业（4分）

2.1 题目1：7-1 jmu-字符串是否对称（20 分）

2.2 设计思路（伪代码或流程图）

    定义两个 字符变量，str[]存放输入的字符串，e;
    int一个变量flag=0辅助判断字符串是否对称
           e=str的栈顶元素
           输入str；
          for(i=0;str[i]!=0;i++)
         遍历str;
          如果str!=e{
           flag=1;
               输出no
          }
           else
           输出yes;

2.3 代码截图（注意，截图、截图、截图。代码不要粘贴博客上。不用用···语法去渲染）

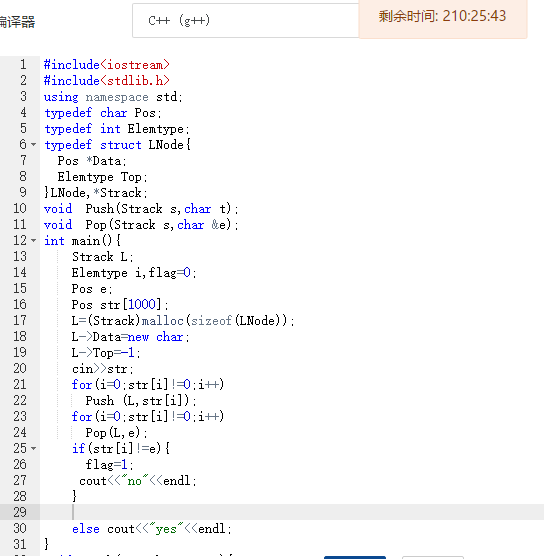
2.4 PTA提交列表说明。

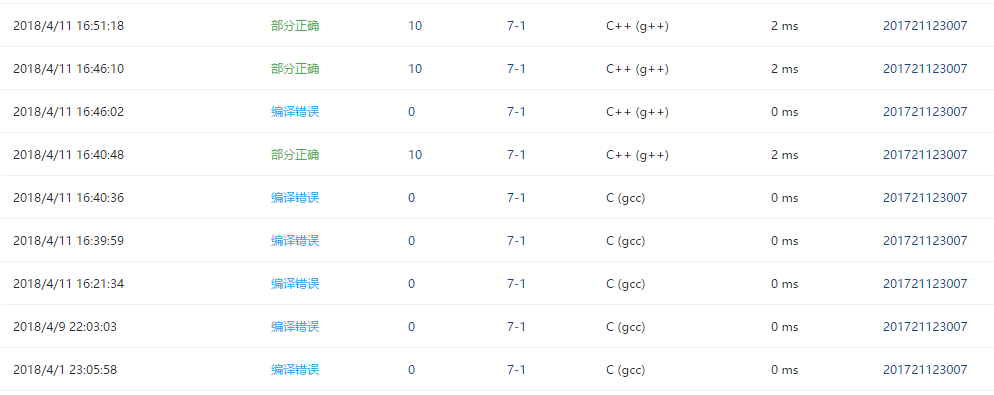
• 1.一开始忘记将Pta的编译器改成c++，所以我这边可以运行，pta那边就是编译错误。
• 2.程序在判断str[i]!=e的语句那里时无法跳出循环，一直输出no，但是加上一个break,就是编译错误，然后就检查可能时前面哪个语句写错了，后面看来看去也没有发现就一直时部分正确。

2.1 题目2：7-3 表达式转换

2.2 设计思路（伪代码或流程图）

   定义数组a,存放表达式
  输入a
  计算出a的长度 lenth
  for i到 lenth{
  根据数字，+,-,*,/ （，）运算优先级不同返回不同的值
   若是数字则直接输出；
   如遇到“（”先输出
    根据前面判断的优先级，高于其优先级则输出
    碰到“）”先输出
    全部运算符都输完之后如果还有元素，再输出
     }

2.3 代码截图（注意，截图、截图、截图。代码不要粘贴博客上。不用用···语法去渲染）

2.4 PTA提交列表说明。

• 一开始是在参考课本代码来写，后来发现课本代码有一个地方，就是struct结构体后面的lpri,rpri后面的符号与数字是什么意思，一直弄不明白，所以后来就到网上查了一下资料，发现思路都是差不多的，但是网上的代码更简洁一些，可是课本代码的逻辑思路我理解了后面也一看就明白就是不懂前面导致不知道该怎么引用，这个却半懂不懂，就是完全不明白它后面在干什么。两个代码都是卡在某个地方没办法灵活运用，后面还需要花点时间再研究一下

2.1 题目2：银行业务队列简单模拟

2.2 设计思路（伪代码或流程图）

    定义两个变量L1,L2存放去两个窗口的顾客，e存放L1返回的值，i，j
    将L1,L2的front,rear初始化为零
       输入n
        for 0到n{
             如果k%2!=0 EnList(L1,k)
             如果k%2==0 EnList(L1,k)
       whileL1,L2不为空{
             如果L1不为空
                    让L1出队列
             如果j!=0
               输出e,j++;}

2.3 代码截图（注意，截图、截图、截图。代码不要粘贴博客上。不用用···语法去渲染）

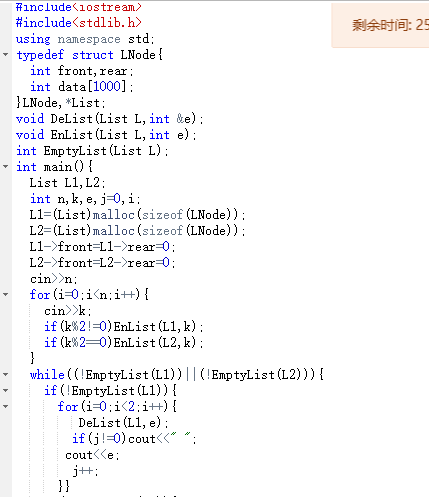
2.4 PTA提交列表说明。

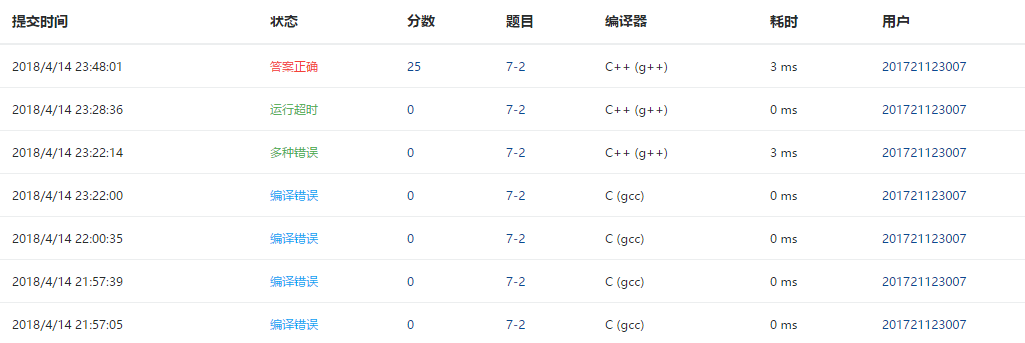
• 一开始的答案错误是在判断函数是否为空时，返回值将“==”写成了“=”，导致答案错误，改正之后可以运行了，但是提交PTA又提示运行超时。
• 后来再仔细看了一下发现，在出队列时我只考虑了L1，没有管L2，因为已经可以运行，就没有注意，PTA提示运行超时之后还以为是什么地方逻辑又错了，没想到是这么大一个逻辑漏洞，下次会好好注意的。

3.截图本周题目集的PTA最后排名（3分）

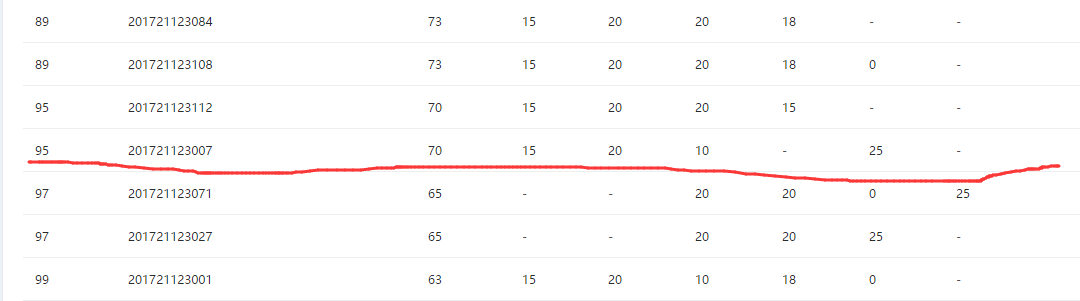
3.1 栈PTA排名

3.2 队列PTA排名

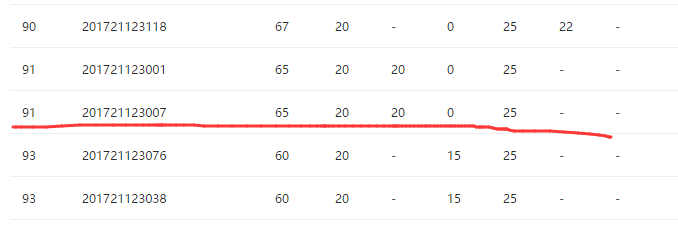
3.3 我的总分：

160

4. 阅读代码（必做，1分）

#include<Windows.h>  
#include<iostream>  
#include <string>  
#include <vector>  
  
using namespace std;  
  
struct sqstack  
{  
    char c[20][10];  
    int top;  
};  
void InitStack(sqstack*s)  
{  
    s->top=-1;  
    for(int i=0;i<20;i++)  
        for (int j=0;j<10;j++)  
         s->c[i][j]='\0';      
}  
BOOL Push(sqstack*s,char e[10])  
{  
    if (s->top==19)  
        return FALSE;  
    s->top++;  
    for (int i=0;i<10;i++)  
        s->c[s->top][i]=e[i];  
    return TRUE;  
}  
BOOL Pop(sqstack*s,char e[10])  
{  
    if (s->top==-1)  
        return FALSE;  
    for (int i=0;i<10;i++)  
        e[i]=s->c[s->top][i];  
    s->top--;  
    return TRUE;  
}  
  
int MidSew(string s,char a[20][10]) //保存中缀表达式  
{  
    int k=0,j=0,e=0;  
    for (int i=0;i<s.size();i++)  
    {  
        if((s[i]!='*')&&(s[i]!='/')&&(s[i]!='-')&&(s[i]!='+')&&(s[i]!='(')&&(s[i]!=')'))  
            k++;  
        else  
        {  
            if (k!=0)  
            {  
                for ( j=i-k;j<i;j++)a[e][j-i+k]=s[j];  
                for (int jjj=k;jjj<10-k;jjj++)a[e][j]='\0';  
                e++;  
                k=0;  
            }  
            a[e][0]=s[i];  
            e++;  
        }  
        if (i==(s.size()-1)&&k!=0)  
        {  
            for ( j=i-k+1;j<=i;j++)a[e][j-i+k-1]=s[j];  
            for (int jj=k;jj<10-k;jj++)a[e][k]='\0';  
            e++;    
            k=0;  
        }  
    }  
    return e;//中缀表达式最终字符数  
}  
  
int BehindSew(char a[20][10],char behd[20][10],int e) //获取后缀表达式  
{  
    sqstack stk;  
    InitStack(&stk);  
    char mid[10];  
    int pp=0;  
    for (int p=0;p<e;p++)  
    {  
        if ((a[p][0]!='*')&&(a[p][0]!='/')&&(a[p][0]!='-')&&(a[p][0]!='+')&&(a[p][0]!='(')&&(a[p][0]!=')'))  
        {  
            for (int i=0;i<10;i++)  
            {  
                behd[pp][i]=a[p][i];      
            }  
            pp++;  
        }  
        else  
        {  
            if (a[p][0]=='(')Push(&stk,a[p]);  
            if (a[p][0]==')')  
            {  
                while (stk.top!=-1)  
                {  
                    if (stk.c[stk.top][0]!='(')  
                    {  
                        Pop(&stk,behd[pp]);  
                        pp++;  
                    }  
                    else  
                    {  
                        Pop(&stk,mid);  
                        break;  
                    }  
                }  
            }  
            if ((a[p][0]=='+')||(a[p][0]=='-'))  
            {  
                while (stk.top!=-1)  
                {  
                    if (stk.c[stk.top][0]!='(')  
                    {  
                        Pop(&stk,behd[pp]);  
                        pp++;  
                    }  
                    else  
                        break;  
                }  
                Push(&stk,a[p]);  
            }  
            if ((a[p][0]=='*')||(a[p][0]=='/'))  
            {  
                Push(&stk,a[p]);  
            }  
        }  
    }  
    while (stk.top!=-1)  
    {  
        Pop(&stk,behd[pp]);  
        pp++;    //最终实际后缀表达式字符数  
    }  
    return pp;  
}  
  
int ResultCount(int pp,char behd[20][10]) //计算结果  
{  
    char mid[10];//中间过渡  
    sqstack stk;  
    InitStack(&stk);  
    for (int u=0;u<pp;u++)  
    {  
        if ((behd[u][0]!='*')&&(behd[u][0]!='/')&&(behd[u][0]!='-')&&(behd[u][0]!='+')&&(behd[u][0]!='(')&&(behd[u][0]!=')'))  
        {  
            Push(&stk,behd[u]);  
        }  
        else  
        {  
            int x=0,y=0;  
            Pop(&stk,mid);  
            x=atoi(mid);  
            Pop(&stk,mid);  
            y=atoi(mid);  
            switch(behd[u][0])  
            {  
            case '-':  
                x=y-x;  
                break;  
            case'+':  
                x=x+y;  
                break;  
            case '*':  
                x=x*y;  
                break;  
            case'/':  
                x=y/x;  
                break;  
            }  
            itoa(x,mid,10);  
            Push(&stk,mid);  
        }  
    }  
    Pop(&stk,mid);  
    return atoi(mid);  
}  
void OutExpression(char behd[20][10],int pp)  
{  
        for (int y=0;y<pp;y++)  
        {  
            if ((behd[y][0]!='*')&&(behd[y][0]!='/')&&(behd[y][0]!='-')&&(behd[y][0]!='+')&&(behd[y][0]!='(')&&(behd[y][0]!=')'))  
                cout<<atoi(behd[y])<<" ";  
            else  
                cout<<behd[y][0]<<" ";  
        }  
}  
int main()  
{  
    string s;  
    cout<<"请输入正确的四则表达式（支持+-*/以及小括号）:";  
    cin>>s;  
    char a[20][10];  
    char behd[20][10];  
    char b[10];  
  
    int c=MidSew(s,a);  
    c=BehindSew(a,behd,c);  
    cout<<endl<<"后缀表达式为：";  
    OutExpression(behd,c);  
    cout<<endl<<endl<<"计算结果为："<<ResultCount(c,behd);  
  
    Sleep(100000);  

• 程序先将我们熟悉的中缀表达式转化为无需括号的后缀表达式，整个思路很清晰，看着很好理解
• 地址https://blog.csdn.net/u010693888/article/details/45669277

5. 代码Git提交记录截图