201871010109-胡欢欢 实验二 个人项目—《求解分组背包问题》项目报告
| 项目 | 内容 |
| ---- | ---- |----|
| 课程班级博客链接 | https://edu.cnblogs.com/campus/xbsf/2018CST |
| 这个作业要求链接 | https://www.cnblogs.com/nwnu-daizh/p/14552393.html |
| 我的课程学习目标 | (1)掌握软件项目个人开发流程。
(2)掌握git工具的使用以及Github发布软件项目的操作方法。
(3)掌握回溯法和初步理解动态规划求解问题的步骤。 |
| 这个作业在哪些方面帮助我实现学习目标 | 首先对我最大的帮助就是让我大致熟悉了软件项目开发的一整个流程,其次就是关于动态规划算法的学习,这使得我的编程能力有所提高。最后就是掌握了github代码仓库的使用方法 |
|项目Github的仓库链接地址|https://github.com/123321hu/DP-|
一. 阅读教师博客“常用源代码管理工具与开发工具”内容要求,点评班级博客中已提交相关至少3份作业
- 相关内容如下:
- 点评1:
链接:https://www.cnblogs.com/chms/p/14550446.html

- 点评2:
链接:https://www.cnblogs.com/xiejinxin/p/14548968.html

- 点评3:
链接:https://www.cnblogs.com/jiangxinxin/p/14522919.html

二. 详细阅读《构建之法》第1章、第2章,掌握PSP流程
相关内容已阅读,基本掌握了PSP流程。
三. 求解 D{0-1} KP问题
1. 需求分析
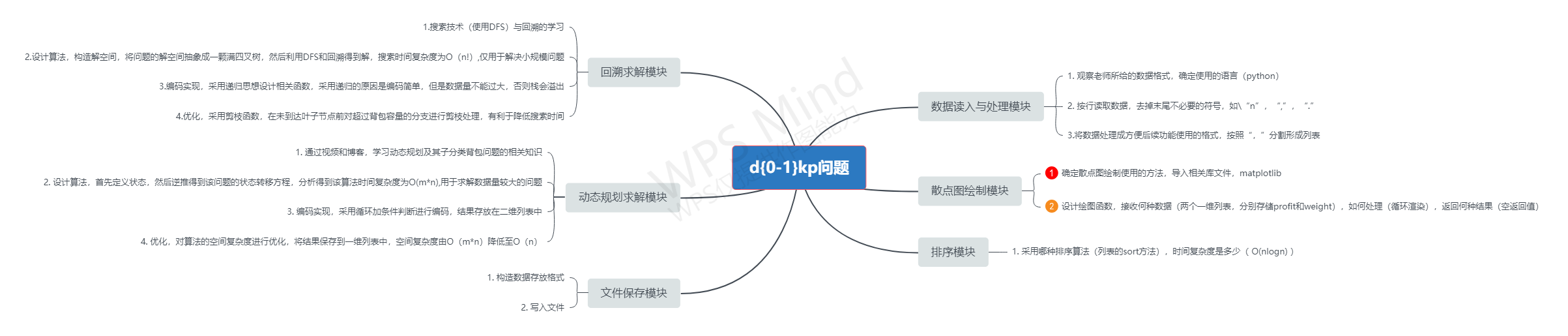
通过对需求文档进行分析,得到系统具有六大模块,分别为:
- 数据读入与处理模块
负责数据读入,并将数据处理成方便其它模块使用的数据格式 - 散点图绘制模块
根据相关数据绘制出以重量为横坐标,价值为纵坐标的散点图 - 排序模块
对各组数据按照项集第三项的价值重量比做非递增排序 - 回溯求解模块
采用回溯法求解不超过背包容量的最大价值和解向量 - 动态规划求解模块
采用动态规划算法求解不超过背包容量的最大价值和解向量 - 文件保存模块
将求解时间,最大价值,解向量保存至txt文件中
2. 功能设计
根据对需求分析的理解,绘制了以下功能设计图:
3. 设计实现
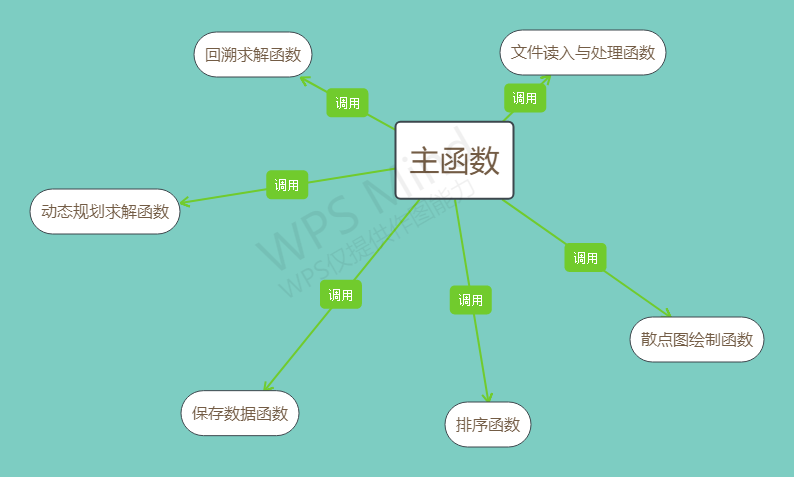
在本模块中,我主要实现了以下函数,函数之间的关系见下图:
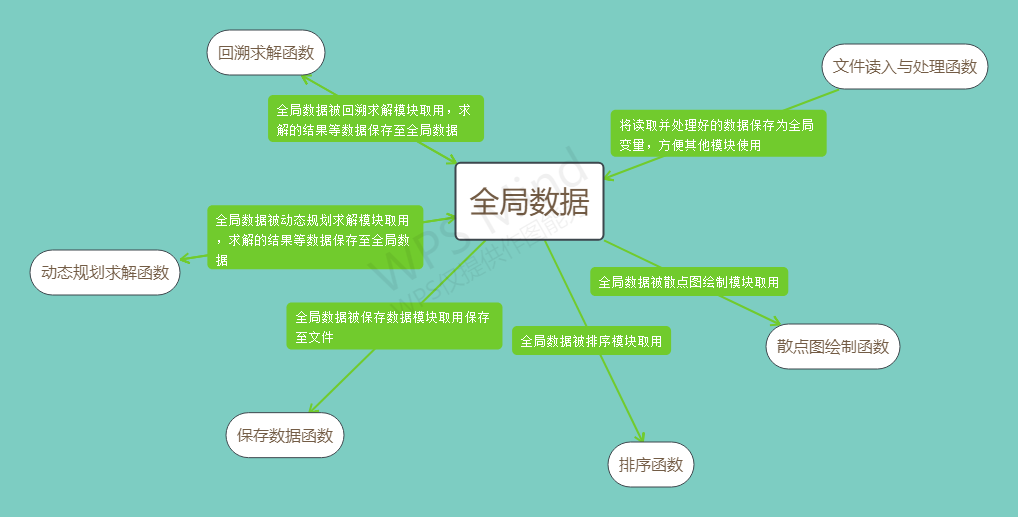
另外,我对数据的使用也做了统一处理,见下图:
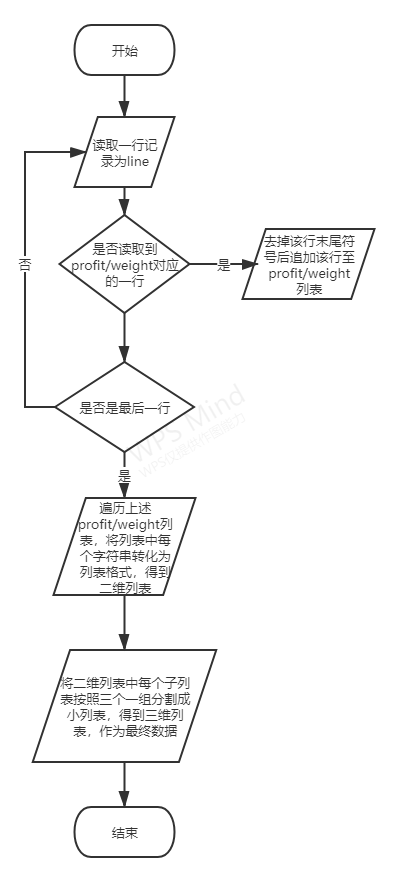
数据处理的好坏直接影响了后续代码的编写,最后,附上数据处理函数的流程图,如下图
4. 测试运行
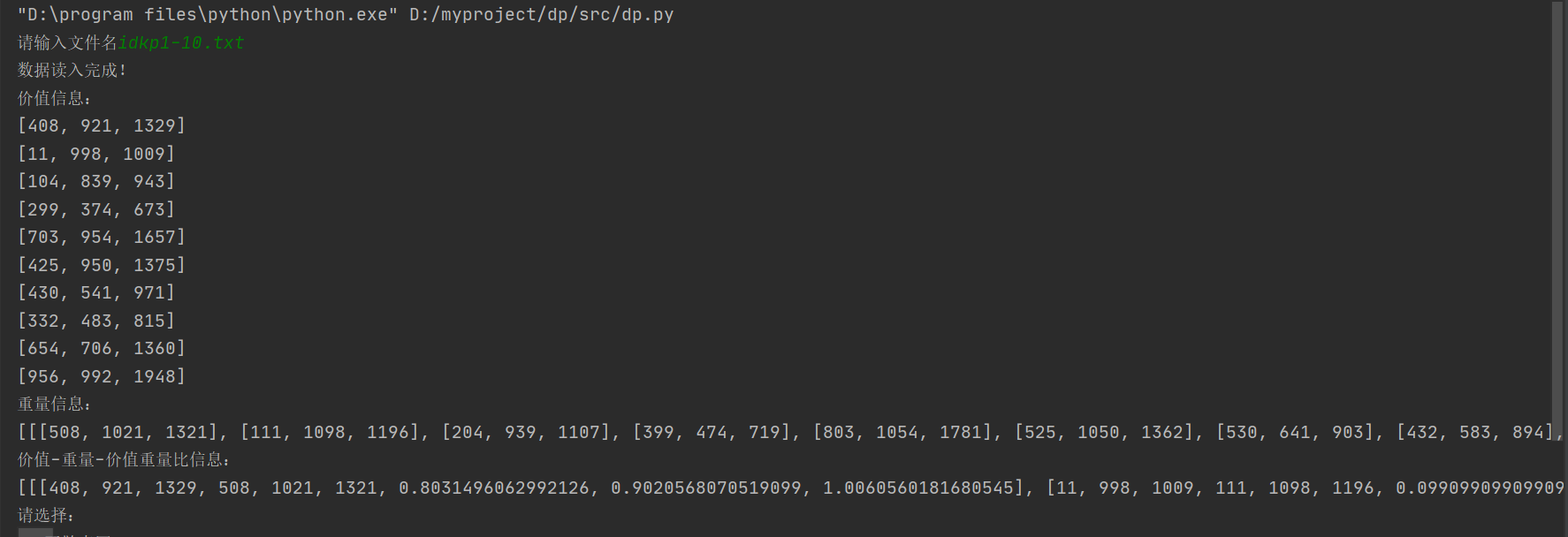
- 数据读取和处理演示与结果如下图:
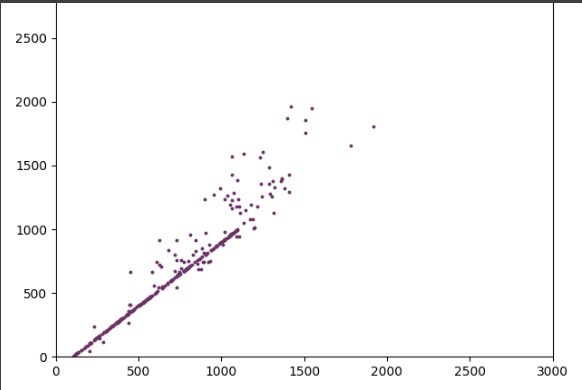
- 散点图绘制如下图,下图是绘制功能的控制台输入信息以及利用idkp1-10.txt中第二组数据绘制的散点图:

- 排序模块演示与结果如下图,下图是对文件idkp1-10.txt中第一组数据按照每个项集第三项的价值重量比非递增排序结果:

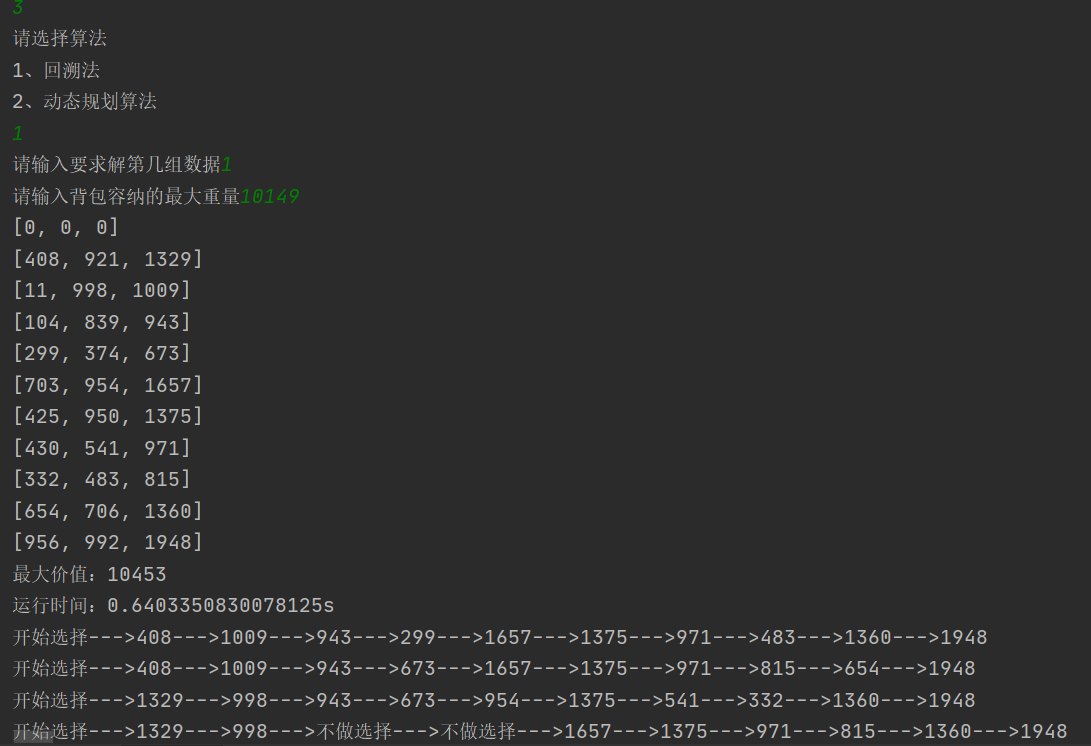
- 回溯算法求解文件idkp1-10.txt中第一组数据演示,如下图
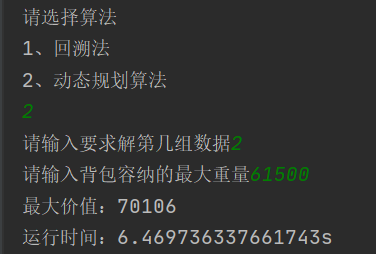
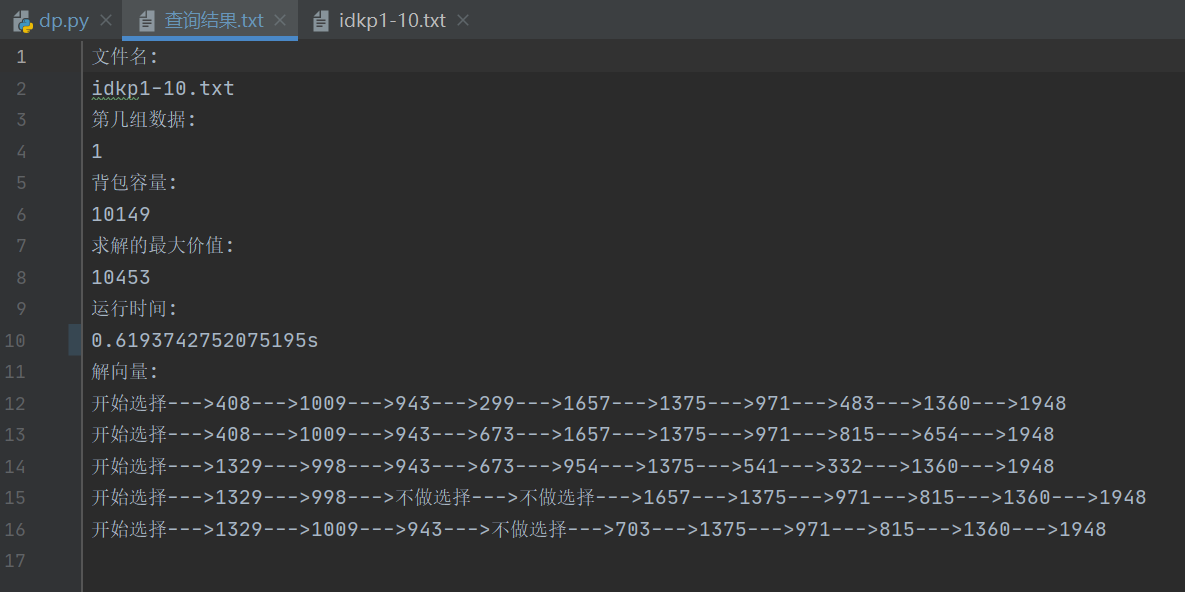
- 动态规划求解文件idkp1-10.txt中第二组数据演示,如下图
- 将回溯法求解文件idkp1-10.txt中第一组数据的求解结果保存,如图
5. 代码展示
本次程序代码使用python语言完成
回溯法求解d{0-1}kp问题代码展示:
# ============================回溯求解模块=================================
# =====================函数功能:访问某节点,并记录已访问节点的总价值和占用背包的总容量
# ==========num:待求解数据下标 maxWeight :背包最大容量 x y totalP当前已经访问的节点总价值 total : 对应的总重量
def huisu(num, maxWeight, x, y, totalP, totalW):
# 每一个项集有0,1,2,3四种状态,等于3则表示在该项集不选物品
if y != 3:
totalP = totalP + profit[num][x][y]
totalW = totalW + weight[num][x][y]
# 搜索到达最底层则回退
if x == len(profit[num]) - 1:
# 打印与保存该条路径的总价值和总重量
if totalW > maxWeight:
# print(totalP)
pathList.append(totalP)
return 0
else:
endMax.append(totalP)
pathList.append(totalP)
return 0
# 未到最底层则继续向下搜索该节点的四个子节点
else:
for i in range(4):
huisu(num, maxWeight, x + 1, i, totalP, totalW)
return 0
动态规划求解d{0-1}kp问题代码展示:
# ===============================动态规划求解模块=================================
# ==========================num:待求解数据的下标 maxWeight:背包最大容量===============================
def dp(num, maxWeight):
# 保存结果的列表
l = []
# 根据下标num取出价值和重量数据
profitArr = []
profitArr = profit[num]
weightArr = []
weightArr = weight[num]
# 初始化结果列表
for i in range(maxWeight + 1):
l.append(0)
# 循环每一组数据
for i in range(len(profit[num])):
# 循环背包容量
for j in range(maxWeight, -1, -1):
# 每一个项集中有多少个数据
for k in range(3):
if j >= weightArr[i][k]:
# 状态转移方程
l[j] = max(l[j], l[j - weightArr[i][k]] + profitArr[i][k])
print('最大价值:' + str(l[maxWeight]))
return str(l[maxWeight])
6. 总结
通过本次实验,我感受到在一个项目的开发中,前期工作是十分重要的。首先要制定清晰明确的工作计划,按照计划去做,会让项目的进行变得井井有条。其次就是需求分析,需求分析的详略程度,需求是否明确等,直接决定了后期编码等工作是否能够顺利进行,在本次项目中,我就是因为在需求分析阶段粗心,忽略了题目中“每个项集的三个项中至多有一个可以被选择装入背包”这一句中的关键字“至多”,进而忽略了某组项集也可以一个物品都不选择这种情况,导致了后期编码完成后的返工,所幸改动不大,但这次事故提醒我,以后在做需求分析时,一定要认真!认真!认真!重要的事情说三遍,最后就是编码时命名一定要规范,注明变量所表示的含义,否则不但自己编码容易出错,别人读起来也会觉得晦涩难懂。
7. 展示PSP
| PSP2.1 | 任务内容 | 计划共完成需要的时间(h) | 实际完成需要的时间(h) |
|---|---|---|---|
| Planning | 计划 | 0.5 | 0.5 |
| nbsp; Estimate | 估计这个任务需要多少时间,并规划大致工作步骤 | 0.5 | 0.5 |
| Development | 开发 | 20 | 29.5 |
| nbsp; Analysis | 需求分析(包括学习新的技术) | 8 | 14 |
| nbsp; Design Spec | 生成设计文档 | 1 | 1 |
| nbsp; Design Review | 设计复审 | 0.5 | 0.5 |
| nbsp; Coding Standard | 代码规范(为开发制定合适的规范) | 1 | 0.5 |
| nbsp; Design | 具体设计 | 0.5 | 0.5 |
| nbsp; Coding | 具体编码 | 6 | 10 |
| nbsp; Code Review | 代码复审 | 1 | 0.5 |
| nbsp; Test | 测试(自我测试,修改代码,提交修改) | 2 | 2.5 |
| Reporting | 报告 | 2 | 1.2 |
| nbsp; Test Report | 测试报告 | 1 | 0.5 |
| nbsp; Size Measurement | 计算工作量 | 0.5 | 0.2 |
| nbsp; Postmortem & Process Improvement Plan | 事后总结 ,并提出过程改进计划 | 0.5 | 0.5 |
经验分享:
在PSP展示环节,通过对预计时间和实际所用时间的统计,我得到了以下几点感悟:
1、通过对比统计的数据,我发现自己的需求分析实际花费时间要比预计时间多得多。在平时,一提到软件项目我们往往最先想到的就是写代码,但通过实际的完成一个项目我发现需求分析阶段才是整个软件项目开发过程中最费时费力的,而且需求分析好与不好也直接决定着后期编码时的工作量和时间
2、测试阶段是软件交付使用前的最后一个阶段,因此软件测试决定了用户的体验,在这一阶段我们通常就是找bug,解决bug,优化算法降低复杂度,目的就是为了提高软件的易用性,改善用户体验
四. 完成任务3的程序开发,将项目源码的完整工程文件提交到Github项目仓库中。
该任务已完成,详情见:https://github.com/123321hu


 浙公网安备 33010602011771号
浙公网安备 33010602011771号