回溯法分析题

2019-04-24

东 华 大 学

《算法设计分析与综合实践》分析题作业

 

学生姓名：曹晨 学号：171310402

1. 作业题目

   旅行售货员问题的费用上限

   设G是一个有n个顶点的有向图，从顶点i发出的边的最大费用记为max(i)。

   1. 证明旅行售货员回路的费用不超过。
   2. 在旅行售货员问题的回溯法中，用上面的界作为bestc的初始值，重写该算法，并尽可能的简化代码。
2. 解题过程（针对算法设计题）
3. 简明扼要地写出解题思路或算法设计思路。可用文字、图等描述
   1. 证明：旅行售货员的回路有很多种解，假设有四个节点分别是ABCD，按照可行的一种顺序B D A C 的求解费用，其费用为，推广都所有解的情况，按照节点经过的顺序编号为1，2，3，4，其费用为，再推广到n个节点的情况。由此可以看出
   2. 在回溯法中，旅行售货员算法中的bestc的初始化为NoEdge，现将其修改bestc=。

    

4. 写出算法描述（要有每个步骤加数字标号，必要的地方加注释，注释用双斜杠//表示），例如：

   输入：

   4

   0 30 6 4

   30 0 5 10

   6 5 0 20

   4 10 20 0

   输出：

   1à3à2à4à1

   25

   

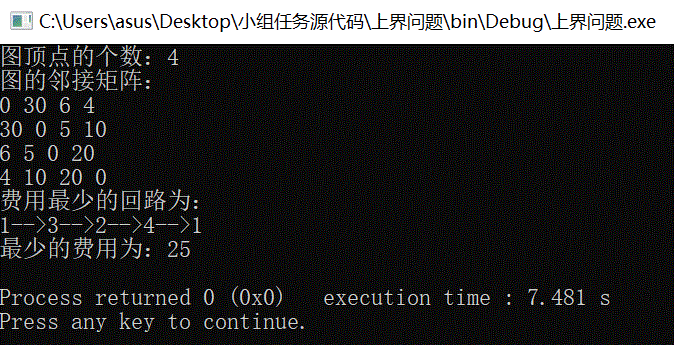
   算法描述如下：

   算法包括定义一个类，类里有三个函数，一个构造函数，一个递归函数，一个求bestc的函数如下

   1 template <class ElemType>
   
   2 class Travelling{
   
   3 public:
   
   4 Travelling(int nw,ElemType **ai,ElemType no)//构造函数
   
   5 {
   
   6 n=nw;
   
   7 for(int i=1 to n)
   
   8 for(int j=1 to n)
   
   9 a[i][j]=ai[i][j];
   
   10 NoEdge=no;
   
   11 }
   
   12 ElemType CalSum();//初始化bestc并调用递归函数的函数
   
   13 private:
   
   14 void Recursive(int i);//递归寻找可行回路的函数
   
   15 int n;//图的顶点数
   
   16 int *x;//当前解
   
   17 int *bestx;//当前最优解
   
   18 ElemType **a;//图的邻接矩阵
   
   19 ElemType s;//当前费用
   
   20 ElemType bestc;//当前最优值
   
   21 ElemType NoEdge;//无边标记
   
   22 };
   
   23 void Travelling<ElemType>::Recursive(int i)
   
   24 {
   
   25 if(i到达第n层即搜索到叶子结点)
   
   26 {
   
   27 if(城市x[n-1]可以到达城市x[n]，并且城市x[n]可以回到城市1，且此时所走的路程s加上x[n-1]与x[n]的距离和x[n]与1的距离小于当前最优值bestc)
   
   28
   
   29 {
   
   30 for(int j=1 to n)
   
   31 bestx[j]=x[j];//保存当前最优解的顺序
   
   32 bestc=s+a[x[n-1]][x[n]]+a[x[n]][x[1]];//记录当前最优解的值
   
   33 }
   
   34 }
   
   35 else
   
   36 {
   
   37 for(int j=i to n)
   
   38 if(城市x[i-1]能达到城市x[j]即这两个城市间有边，并当前所走的路程s加上这两个城市的距离比当前最优值bestc小)
   
   39 {
   
   40 swap(x[i],x[j]);
   
   41 s+=a[x[i-1]][x[i]];//修改此时所走的路程s,进入下一层递归
   
   42 Recursive(i+1);
   
   43 s-=a[x[i-1]][x[i]];//恢复原来cc的值
   
   44 swap(x[i],x[j]);
   
   45 }
   
   46 }
   
   47 }
   
   48 ElemType Travelling<ElemType>::CalSum()
   
   49 {
   
   50 int maxi;
   
   51 bestc=1;//初始化为1
   
   52 for(int i=1 to n)
   
   53 for(int j=1 to n)
   
   54 if(a[i][j]>maxi)//遍历找到从节点i发出的最大费用的边
   
   55 maxi=a[i][j];
   
   56 if(maxi!=NoEdge)//如果没有
   
   57 return NoEdge;//直接返回无边标记
   
   58 bestc+=maxi;//否则加紧bestc
   
   59 for(int i=1 to n)
   
   60 x[i]=i;
   
   61 bestx[i]=i;//初始化x和bestx的顺序
   
   62 s=0;//初始化当前费用
   
   63 Recursive(2);//从第二层开始递归求回路
   
   64 return bestc;
   
   65 }

    

    

5. 算法分析：

   时间复杂度：

   在函数CalSum中,两个嵌套的for循环用来求bestc的初始值，一个for循环来初始化x和bestx，总时间为f(n)=n+n*n=O(n)。在函数Recursive中，在最坏的情况下可能需要更新当前最优解O((n-1)!)，每次更新bestx需要O(n)计算时间，从而整个算法的时间复杂度为O((n)!);

   空间复杂度：

   图的邻接矩阵用了一个二维数组，当前解和最优解分别用了两个一维数组，所以f(n)=n*n+n*2=O(n² ),算法的空间复杂度维O(n² )

代码见打包文件