动态规划分析题
东 华 大 学
《算法设计分析与综合实践》分析题作业
学生姓名: 曹晨 学号:171310402
请勿转载或抄袭
- 作业题目
二维0-1背包问题
给定n种物品和一背包,物品i的重量是wi,体积是bi,其价值为vi,背包的容量为c,容积为d。问应如何选择装入背包的物品,使得装入背包中的物品总价值最大?在选择装入背包的物品时,对每种物品i只有两种选择,即装入背包和不装入背包。不能将物品i装入背包多次,也不能只装入部分的物品i。试设计一个解决问题的动态规划算法,并分析算法的计算复杂性。
- 解题过程(针对算法设计题)
- 解题思路或算法设计思路。
这个问题和一维的背包问题类似,同样具有最优子结构性质,只需将二维数组变成三维数组来考虑两个变量的情况下的解法。其子问题的最优值为m[i][j][h],即背包容量为j,容积为h,可选择的物品为i,i+1,…,n时背包问题的最优值。由背包的最优子结构可以建立计算m[i][j][h],即m[i][j][h]=max(m[i-1][j][h],m[i-1][j-w[i-1]][h-b[i-1]]+v[i-1]);按照这个递归可以算出m(n,c,d)的最优值。
- 算法描述
算法描述如下:
//用于计算最优值的函数
1 int Knapsack(int c,int d,int***m,int *v,int w*){
2 for(i=1 to n)
3 for(j=0 to c)
4 for(h=0 to d)//三重循环遍历当容积为h容量为j时前0-i个物品的最优值
5 if(h>=b[0]&&j>=w[0])
6 m[i][j][h]=max(m[i-1][j][h],m[i-1][j-w[i-1]][h-b[i-1]]+v[i-1]);
7 for(i=1 to n)//遍历数组,找到最大值即为最大价值数
8 maxo=max(maxo,m[i][c][d])
9 return maxo
10 }
//用于求具体放入哪些物品时的函数
1 void Traceback(int ***m,int c,int d,int n)
2 {
3 for(i=n to 1)//遍历数组,反过来求最优解时装入的物品。
4 if( if(m[i][c][d]==m[i-1][c][d]))
5 x[i-1]=0;
6 else{
7 x[i-1]=1;
8 c=c-w[i-1];
9 d=d-b[i-1]
10 }//当第i件物品和第i-1件物品(容量和容积均减去第i件物品对应的指数)的最优解值相同时,没放入,否则放入背包里了
11 x[0]=(m[0][c][d])?1:0;//第一件物品没法和上一件比,当此时容积和容量的大小有一个小于到第一个物品的体积和重量,则第一个没放入
12 }
输入:
个数:5
容量:8
容积:7
5个物品的重量、体积和价值:
3 2 6
4 1 5
6 4 7
1 1 3
2 4 8
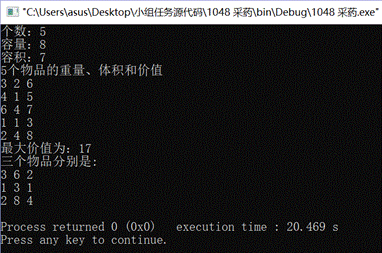
输出:
最大价值为:17
三个物品分别是:
3 6 2
1 3 1
2 8 4
- 算法分析:
时间复杂度:
用了三个叠套的for循环来寻找子问题的最优解,用了一个for循环来求最大值,一个for循环来求最优解时放入背包的物品,一个for循环来输出放入的物品。
f(n)=ncd+n+n+n=ncd+3n=O(ncd);
空间复杂度:
由于采用了三位数组来存储子问题的最优解,三个一维数组来存储每个物品的重量体积和价值,一个一维数组来存储在最优解时是否放入背包
f(n)=ncd+n+n+n+n=ncd+4n=O(ncd);



