分治法之众数问题
东 华 大 学
《算法分析设计与综合实践》实验报告
学生姓名:曹晨 学号:171310402 指导教师:章昭辉
实验时间:2019-3-13 实验地点:图文信息楼三号机房
请勿转载!!!
- 实验名称
众数问题
-
实验目的
对于给定的由n个自然数组成的多重集S,计算S的众数及其重数。
-
实验内容
给定含有n个元素的多重集合S,每个元素在S中出现的次数称为该元素的重数。多重集合S中重数最大的元素称为众数。例如{1,2,2,2,3,5}。多重集合S的众数为2,其重数为3。
数据输入:
输入第一行为多重集S中元素的个数n;在接下来的n行中,每行有一个自然数。
结果输出:
输出由两行,第一行为众数,第二行时重数
-
实验过程
自己的思路:
创建一个数组b[][2],遍历一遍数组,b中的结果如下
元素
个数
b[0]
1
1
b[1]
2
3
b[2]
3
1
b[3]
5
1
在数组b中找到个数最多的值为重数,对应的元素为众数,输出即可
参考答案及网上的思路:
|
1 |
2 |
2 |
2 |
3 |
5 |
l med r
👇
|
1 |
2 |
2 |
2 |
3 |
5 |
l l1 med r1 r
左子集 右子集
|
1 |
3 |
5 |
l,r l r
‧‧‧‧‧‧‧‧‧
每做完一次上述的操作,都要更新一下众数和重数。当重数的大小大于左(或右)子集的大小时,就不用在左(或右)子集中再做一次上述操作。
-
结果分析
这个结果是我用数组的办法编写的。所用的时间为9.683s
这个结果是我用分治法的办法编写的。所用的的时间为5.352s
由此可见,用分治法解这道题效率更高
-
实验总结
刚开始我没有想到可以用分治法来做,用的是数组来做。做完以后发现算法太过复杂,而且处理较大的n时,时间复杂度和空间复杂度都比较大。于是我参考了算法答案那本书,学到了分治法来解决这道题。但是在完成了用分治法的代码以后,我发现了问题:
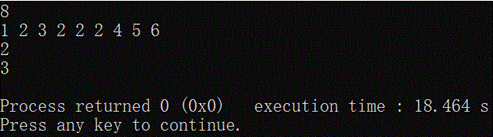
输出应该为:
2
4
分治法解决这道题有一个大前提:多重集中的元素是有序的(递增或者递减),所以很有必要给多重集加入一个排序的算法.
附录:(要求代码里各行要有注释)
自己的代码(性能不够好,太过复杂)
int main()
{
int n;
cin>>n;
int a[n];
for(int i=0;i<n;i++)
{
cin>>a[i];
}
f(n,a);
return 0;
}
void f(int n,int *a)//n为多重集元素的个数,a是存放数组的元素
{
int b[n][2];//b[][0]存放元素的种类,B[][1]存放每种元素的个数
b[0][0]=a[0];
b[0][1]=1;
int h=0;//数组b中已初始化的行的标号
int flag=0;//判断b中是否已经有该元素了
for(int i=1;i<n;i++)
{
for(int j=0;j<=h;j++)
{
if(a[i]==b[j][0])//判断元素a[i]是否已经在数组b中存在
{
b[j][1]++;
flag=1;
}
}//存在的话,把b[j][1]加1,flag变为1,否则不做操作
if(flag==0)
{
h++;
b[h][0]=a[i];
b[h][1]=1;
}
flag=0;
}//不存在的话,flag为0,此时把a[i]加入到数组之中,并把个数变为1
int temp=b[0][1];
int t=0;
for(int i=0;i<=h;i++)//寻找b中数目最多的那个元素
{
if(temp<b[i][1])
{
temp=b[i][1];
t=i;
}
}
cout<<b[t][0]<<endl<<temp<<endl;//输出众数和重数
}
参照答案和csdn博客所改的代码:
https://www.cnblogs.com/yangykaifa/p/7162192.html
https://blog.csdn.net/chencong3139/article/details/52863629
int main()
{
int n;
cin>>n;//元素个数
int a[n];
for(int i=0;i<n;i++)
{
cin>>a[i];
}//数组用于存放元素
int l=0;//数组的首个标号
int r=n-1;//数组的最后一个标号
int largest=0;//重数的初始化
int elem=-1;//众数的初始化
mode(a,l,r,largest,elem);//调用函数
cout<<elem<<endl<<largest<<endl;//输出众数和重数
return 0;
}
//用于求数组的中位数的函数↓
int median(int *a,int l,int r)
{
return a[(l+r)/2];
}
//以med来划分数组↓ !!!关键函数
void split(int *a,int med,int l,int r,int &l1,int &r1)
{
for(l1=l;l1<=r;l1++)
{
if(a[l1]==med)
break;
}//l1表示首个等于med的数组下标
for(r1=l1+1;r1<=r;r1++)
{
if(a[r1]!=med)
break;
}
r1--;
}//r1表示最后一个等于med的数组下标
void mode(int *a,int l,int r,int &largest,int &elem)
{
int l1,r1;//分割后左边子数组的右界和右边子数组的左界
int med=median(a,l,r);//midian函数用于找到数组的中位数
split(a,med,l,r,l1,r1);//以med中位数来分割数组
if(largest<r1-l1+1)
{
largest=r1-l1+1;
elem=med;
}//每次递归更新众数和重数的值
if(l1-l>largest)
mode(a,l,l1-1,largest,elem);//判断左边是否值得递归(只有l1-1大于largest才有必要搜寻)
if(r-r1>largest)
mode(a,r1+1,r,largest,elem);//判断右边是否值得递归
}



