博客作业—图

1.学习总结

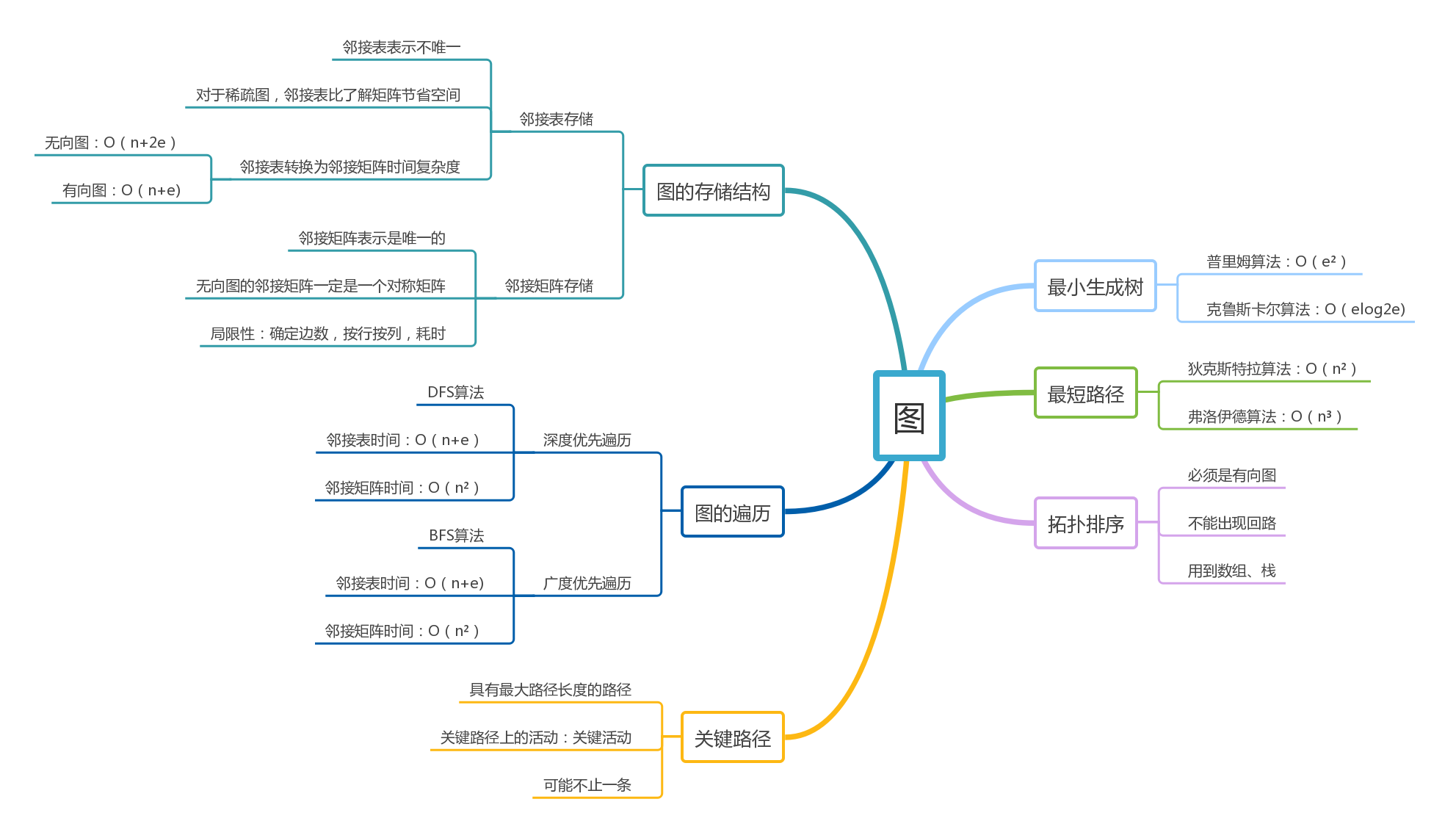
1.1图的思维导图

1.2 图结构学习体会

谈谈你对图结构中的几个经典算法学习体会。具体有：

• 深度遍历算法和广度遍历算法：理解起来相对容易，尤其是在邻接矩阵中，找起来很方便，重要的就是要细心，做到不重不漏
• Prim和Kruscal算法：prim算法把顶点分成已选和未选的思路很好，但相比来说kruscal算法找最小边更为精确，代码量也小
• Dijkstra算法：时间复杂度为O（n²），要很认真地去观察新添顶点后，点与点之间的距离能不能更小
• 拓扑排序算法：一定要有向图，要去判断有没有环路，有环路则为错误

2.PTA实验作业

---

1.1 题目1：7-1 图着色问题

1.2 设计思路

图着色问题是一个著名的NP完全问题。给定无向图,，问可否用K种颜色为V中的每一个顶点分配一种颜色，使得不会有两个相邻顶点具有同一种颜色？

但本题并不是要我们解决这个着色问题，而是对给定的一种颜色分配，判断这是否是图着色问题的一个解。

重点代码流程为：使用回溯法将visited数组初始化为0-->依次观察每一种颜色，若顶点之间的着色不冲突则转下一步骤，否则继续搜索-->若顶点全部着色，输出数组

-->若顶点是一个合法着色，则转处理下一个-->否则重置顶点颜色

1.3 代码截图

1.4 PTA提交列表说明

 

 

说明：主要是细节处理问题，自己应该清楚每个循环结构体开始和结束的地方！！！

---

2.1 题目2：7-2 排座位

2.2 设计思路

题目关于敌对和朋友问题说的很拗口，但简化起来：关系为1表示是朋友，-1表示是死对头--->朋友两顶点的权值为1，死对头两顶点权值为-1；

如果两位宾客之间是朋友，且没有敌对关系，则输出No problem；如果他们之间并不是朋友，但也不敌对，则输出OK；如果他们之间有敌对，然而也有共同的朋友，则输出OK but...；如果他们之间只有敌对关系，则输出No way。---->权值为1，No problem；没有连接，OK；有共同根，OK but...;权值为-1，No way。代码主要就是建图和判断两点关系。

2.3 代码截图

2.4 PTA提交列表说明

说明：没注意看清输出要求里面大小写和点，以后要认真审题！！！

3.1 题目3:7-5 畅通工程之最低成本建设问题

3.2 设计思路

成本问题就是最短路径问题，用最小生成树来求解问题，由输入数据建立带权的无向图，判断两顶点（两城镇）的

最短路径（最低成本建设）。

3.3 代码截图

3.4 PTA提交列表说明

 说明：对Prim算法的熟练度不够，改动课本源代码比较慢。

3.截图本周题目集的PTA最后排名

 

4. 阅读代码

六度空间是一个看似复杂的大数据结构，但经过图结构的简化，将人与人的关系建立起来，

更好地判断他们的关系，足以见得图结构的优势

1. #include<stdio.h>  
2. #include<malloc.h>  
3. #define MAX 10001//最大顶点数   
4. /** 
5. *解题思想： 
6. *对图进行广度搜索 
7. *得出每层中的顶点数 
8. *计算百分比 
9. */  
10. int BFS(int i, int N, int ** snap)  
11. {//       队列      遍历登记       队头  队尾  计数器 层数  
12. int q[MAX], visit[MAX], front, rear, count, level, last, tail, v, j;  
13. for (j = 0; j < 10001; j++)//初始化数组   
14. visit[j] = 0;  
15. visit[i] = 1;//开始结点   
16. front = rear = -1;//队列初始化   
17. count = 1;//计算六度空间的个数  
18. level = 0;//level计算层数，等于6时跳出  
19. last = i;//last为上一层最后的顶点  
20. q[++rear] = i;//入队 当前顶点所在层数  
21. while (front<rear) //遍历队列（六层以内）   
22. {  
23. /* 
24. *图的广度搜索原理解析： 
25. *类似二叉树的层序遍历 
26. *1、从所需要的顶点进入图（类似利用此顶点为树的根结点，构建一棵树） 
27. *2、根结点入队列 
28. *3、寻找与此顶点相连的所有顶点并放入队列中（图的临接矩阵中，储存的是每个顶点间的边的关系，而且无向图的临接矩阵一定为对称矩阵） 
29. *4、当顶点所在行遍历结束，取出队列的下一个顶点，重复。直至遍历所有的顶点 
30. */  
31. v = q[++front]; //出队   
32. for (j = 1; j <= N; j++)//遍历   
33. if (!visit[j] && snap[v][j] == 1)  
34. {//当结点没有记录而且此处结点为顶点时   
35. q[++rear] = j;//入队列   
36. visit[j] = 1;//记录对应位置   
37. count++;//计数器   
38. tail = j;//tail是当前层的最后一个顶点  
39. }  
40. if (v == last)  
41. {  
42. level++;//层数加一   
43. last = tail;//记录最后一个顶点   
44. }  
45. if (6 == level)//等于六层时，退出循环   
46. break;  
47. }  
48. return count;//返回六度空间内所有顶点数  
49. }  
50. int main(void)  
51. {  
52. int N, M;  
53. int count = 0;  
54. scanf("%d %d", &N, &M);  
55. int **snap;//实现动态分配二维数组  
56. /*注意： 
57. *******动态分配必须按照顺序分配 
58. *******同时数组释放内存的时候要按照先后顺序释放 
59. *******否则会出现野指针 
60. *******内存泄漏导致程序崩溃 
61. */  
62. snap = (int**)malloc(sizeof(int*) * (N + 1));  
63. if (snap == NULL)  
64. return -1;  
65. //动态分配内存存在失败的可能，所以  
66. //在进行动态分配内存后  
67. //应该进行对应的指针是否为空指针的判断   
68. int i, x, y, j;  
69. for (i = 0; i <= N; i++)  
70. {  
71. *(snap + i) = (int *)malloc(sizeof(int) * (N + 1));  
72. if (*(snap + i) == NULL)  
73. return -1;  
74. }  
75. for (i = 0; i < M; i++)  
76. {  
77. scanf("%d %d", &x, &y);//无向图对角线对称   
78. snap[x][y] = snap[y][x] = 1;//关系对等  
79. }  
80. for (i = 1; i <= N; i++)  
81. {  
82. count = BFS(i, N, snap);  
83. printf("%d: %.2f%%\n", i, (float)count / N * 100);  
84. }  
85. //直接进行头指针的内存释放不全等于所有指针内存的释放   
86. //free(snap);  
87. for (i = 0; i < N; i++)  
88. {  
89. free(*(snap + i));  
90. *(snap + i) = NULL;  
91. }  
92. free(snap);  
93. snap = NULL;  
95. return 0;  
96. }