Beta分布
用例子理解Bbta分布(一)
Beta分布可以看做是分布之上的分布。我们以抛硬币为例,不过,我们并不假设硬币是均匀的(也就是说:并不假设每次抛硬币,正面朝上的概率为0.5),所以抛硬币的正面朝上的概率p是未知的(只知道p∈[0,1])。如果进行一次二项分布试验,在这次二项分布试验中,抛硬币10000次,其中正面朝上7000次,反面朝上3000次,我们可以得到,正负面朝上的概率分别为{p,1-p}={0.7,0.3}。但是我们并不确信这个结果是正确的。我们想要做10000次二项分布试验,在每次二项分布试验中,均抛硬币10000次(说不定在其他二项分布实验中,得到的正负面朝上的概率是{0.2,0.8}或者{0.6,0.4},这些情况都有可能),那么,我们想要知道,在这样的多次重复二项分布实验中,抛硬币最后得到正负面朝上概率为{0.7,0.3}这样概率为多少?这就是在求抛硬币的概率分布之上的分布。这样的分布就叫做Beta分布。正如二项分布可以看做多次进行伯努利试验所得到的分布一样,Beta分布也可以看做是多次进行二项分布的试验所得到的分布,是分布之上的分布。
用例子理解Bbta分布(二)
有一枚硬币(不知道它是否公平),假如抛了三次,三次都是“花”,能够说明它两面都是“花”吗?
1. 贝叶斯推断
按照传统的算法,抛了三次得到三次“花”,那么“花”的概率应该是:P = 3/3 = 100%。但是抛三次实在太少了,完全有可能是运气问题。我们应该怎么办?
贝叶斯认为在实验之前,应根据不同的情况对硬币有所假设。不同的假设会得到不同的推断。
比如和滑不溜手的韦小宝玩。韦小宝可能拿出各种做过手脚的硬币,让我们猜不透,只能假设对硬币一无所知。这种假设之下,我们就只能根据实验结果来猜测。因此,实验结果是“扔三次,三次花”,倾向于认为韦小宝有可能作弊:

大侠陈近南用的可能是公平硬币:

而憨坏的多隆,真的有可能用两面“花”来和你玩:

各种假设称为先验分布,结合刚才“扔三次,三次花”的实验数据,推断出硬币的后验分布,这就是贝叶斯推断:

2.Beta分布
那么问题来了,“先验分布”,“后验分布”用数学怎么表示?对于扔硬币,Beta分布非常适合用来完成这个任务。
2.1 先验分布
Beta分布简记为:Beta(a,b),根据a,b参数的不同,形态各异:
在韦小宝面前,我们对硬币一无所知。贝叶斯说,一无所知也就是意味着任何概率都是一样的,都是有可能的,所以选用均匀分布。Beta(1,1)正好就是均匀分布:
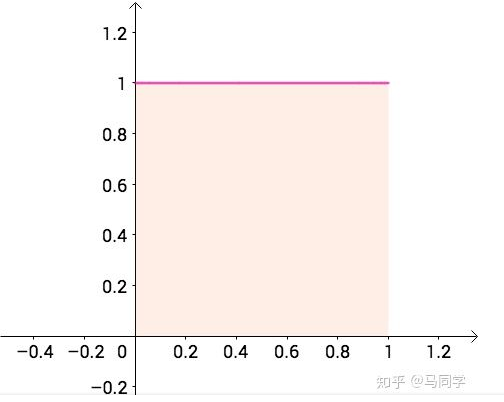
正直的陈近南,可能用的是公平硬币,也就是说概率在0、1之间(0表示“字”,1表示“花”),Beta(5,5,)可以表示这样的分布:
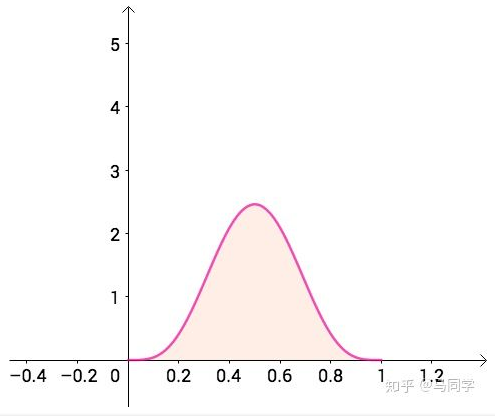
而憨坏的多隆,可能用了两面花,也就是说概率可能集中到1附近,Beta(5,1)可以表示这样的分布:
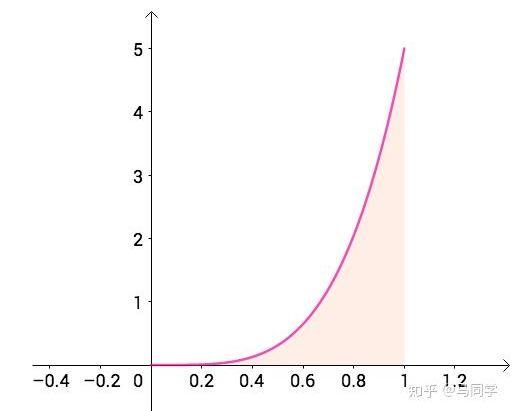
也就是说可以用Beat 分布来模拟各种先验分布:
一无所知:Beta(1,1)
公平硬币:Beta(5,5)
两面花:Beta(5,1)
2.2 后验分布
用Beta分布来模拟扔硬币的先验分布之后,通过贝叶斯推断,得到的后验分布依然是Beta分布:

具体到这个例子:
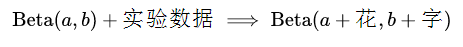
再具体到韦小宝的情况就是:
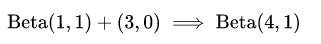
图像上的变化就是:
可以看到,作弊的可能性还是比较大的。
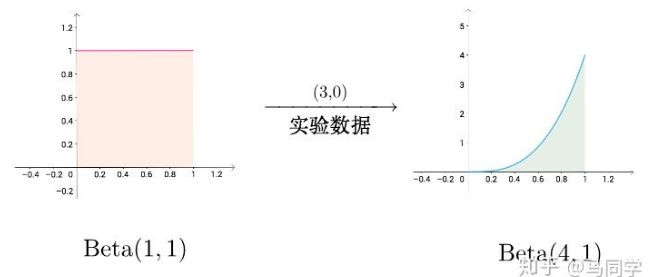
陈近南的情况:
结合试验数据之后,图像的中心从0.5往0.6方向移动了,作弊可能性有所增加,不过总体来看应该还是公平硬币的可能性大。
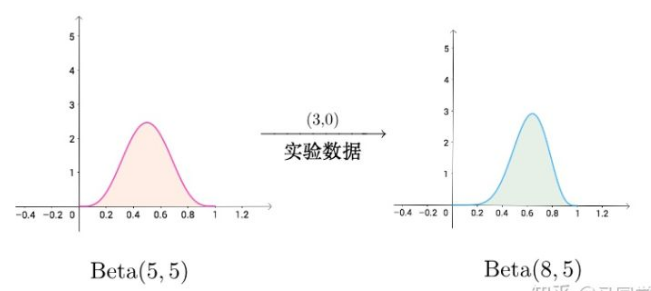
多隆的情况:
更向1集中,作弊的可能性非常高。
3 代数细节
3.1 贝叶斯推断
贝叶斯推断:

的应用到二项式分布的数学细节如下。假设实验数据 服从二项分布:
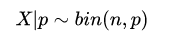
上面的式子根据贝叶斯定理可以表示为:
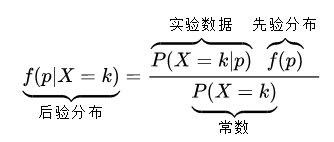
其中 为“花”的次数。分母与实验数据无关,可以视作常数:
因此,写成下面这样更容易看清楚重点(其中 表示两者之间成比例):

3.2 Beta分布


3.3 共轭先验
对于二项式分布,用Beta 分布作为先验分布,通过贝叶斯推断之后,后验分布依然是Beta分布:
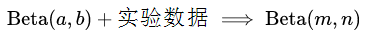
这种特性称为共轭先验。
参考资料:
伯努利分布、二项分布、Beta分布、多项分布和Dirichlet分布与他们之间的关系,以及在LDA中的应用【存疑】



