2021 上海 ICPC 区域赛
签到题：EDGI
铜题：H
银题：JKM
金牌：B
D Strange Fractions
设 \(x = {a \over b}\)，那么有 \({p\over q} = x + {1 \over x}\) ，可以转换为求解 \(qx^2-px+q = 0\) 的正整数根。
使用求根公式，判断 \(p^2-4*q^2\) 是否是完全平方数即可。然后取 \({a\over b}={p+d\over 2q}\) 。复杂度 \(O(T\log q)\)
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
int T;
ll p, q;
int main(){
scanf("%d", &T);
while(T--){
scanf("%lld%lld", &p, &q);
ll d = p * p - 4 * q;
if(d < 0) {
puts("0 0");
} else {
ll t = sqrt(d);
if(t * t == d) printf("%lld %lld\n", p + t, 2 * q);
else puts("0 0");
}
}
}
E Strange_Integers
整体排序后，贪心的去选即可。证明：设 \(f[i]\) 表示前 \(i\) 个能够选出的最多的个数，那么 \(f[i]\) 随着 \(i\) 递增，求解 \(f[j]\) 时（\(j\gt i\)），去找尽量大的 \(i\) 满足 \(a[j]-a[i] \ge k\) 。
#include <bits/stdc++.h>
using namespace std;
const int N = 100010;
int n, k, a[N];
int main(){
cin >> n >>k;
for(int i=1;i<=n;i++){
scanf("%d", &a[i]);
}
sort(a + 1, a + 1 + n);
int res = 1;
int last = a[1];
for(int i=2;i<=n;i++){
if(a[i] - last >= k) {
last = a[i];
res ++;
}
}
cout <<res <<endl;
return 0;
}
G Edge Groups
\(n\) （奇数）个点的树，\(n-1\) 条边分成 \({n-1\over 2}\) 组，每组两条边并且这两条边要有一个公共点，询问分组的方案数。
考虑树形DP，子树 \(x\) 中若有偶数个点，那么奇数条边必然无法分组，需要 \(x\) 连向其父亲的边。如果有奇数个点，那么偶数条边可以分组。
设 \(d[x]\) 为分组 \(x\) 子树中的边的方案数，设 \(x\) 的孩子 \(y\) 中，有 \(a\) 个 \(y\) 需要 \((x,y)\) 这条边与 \(y\) 子树中的边配对，有 \(b\) 个 \(y\) 是 \((x,y)\) 在 \(x\) 这里配对的。那么当 \(b\) 是奇数时还需要 \(x\) 与其父亲连接的边。
也就是说，\(x\) 有 \(a\) 个子树点数是偶数，\(b\) 个子树点数是奇数。现在只需要考虑把 \(b\) 个子树两两分组即可，如果 \(b\) 是奇数，那么还需要 \((x,fa)\) 加入其中。
\(n\) 个元素，每组两个分成 \({n\over 2}\) 组的方案数是 \(f[n]\)，有递推式 \(f[n] = f[n-2] * (n-1)\) 。
所以：
每个子树的方案数依旧独立，所以累计贡献时还是用乘法，只是其中 \(b\) 个是有顺序的，这个顺序个数就是 \(f\)。
#include<bits/stdc++.h>
using namespace std;
#define rep(i,j,k) for(int i=int(j);i<=int(k);i++)
#define per(i,j,k) for(int i=int(j);i>=int(k);i--)
typedef long long ll;
const int N = 100010, mod = 998244353;
int n, sz[N];
vector<int> g[N];
ll d[N], f[N];
void dfs(int x, int fa){
sz[x] = 1; d[x] = 1;
int cnt = 0;
for(auto &y : g[x]) {
if(y == fa) continue;
dfs(y, x);
sz[x] += sz[y];
d[x] = d[x] * d[y] % mod;
if(sz[y] & 1) cnt ++;
}
if(cnt & 1) cnt ++;
d[x] = d[x] * f[cnt] % mod;
}
int main(){
scanf("%d", &n);
for(int i=1;i<n;i++){
int x, y; scanf("%d%d", &x, &y);
g[x].push_back(y); g[y].push_back(x);
}
f[0] = 1;
for(int i=2;i<=n;i+=2){
f[i] = f[i-2] * (i-1) % mod;
}
dfs(1, 0);
printf("%lld\n", d[1]);
return 0;
}
H Life is a Game
\(n\) 个点 \(m\) 条边，有点权和边权，\(q\) 个询问，每个询问 \(x,k\) 表示从 \(x\) 出发，带着 \(k\) 的能力，通过一条边的条件是能力大于这条边的权值，当第一次到达一个点时可以将该点的权值累加到能力上，求可以获得的最大能力。
考虑离线询问，每个点带有若干个询问，每个询问包含初试能力值和询问ID。然后从小到大枚举每条边\((x,y,w)\)，设 \(v[x]\) 是 \(x\) 的点权，那么对于从 \(x\) 出发的询问，如果能力值 \(k+v[x] < w\)，那么说明它无法到达除去 \(x\) 之外的所有点，它的答案就是 \(k+v[x]\)，紧接着把该询问从 \(x\) 的询问集合中删除。之后对于 \(y\) 做同样的处理。
此时，\(x\) 和 \(y\) 中询问都可以通过 \((x,y,w)\) 这条边，所以，可以将 \(x\) 与 \(y\) 合并成一个集合，然后该集合的点权和就是 \(v[x]+v[y]\)。这里可以用一个带权并查集合并。另外询问也需要合并，按照启发式合并的思想，每次小的集合向大的集合合并即可。
总体复杂度为 \(O(m\log m+q\log ^2 q)\) 。
关于启发式合并的思想简单提一下，每次小的集合向大的集合合并，那么对于小的集合而言，大小扩大二倍以上，所以每个点从小的集合删除再加入大的集合的次数不会超过 \(\log_2^n\)，整体复杂度就是 \(n\log_2^n\)。本题中因为需要对询问按照能力值排序，所以需要用 multiset 维护，所以是两个 log 的复杂度即 \(q\log^2 q\)
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 100010;
int n, m, q;
struct Edge
{
int x, y, w;
bool operator<(const Edge &b) const
{
return w < b.w;
}
} e[N];
int f[N], v[N], rs[N];
multiset<pair<int, int>> st[N];
int get(int x) { return x == f[x] ? f[x] : f[x] = get(f[x]); }
int main()
{
cin >> n >> m >> q;
for (int i = 1; i <= n; i++)
scanf("%d", &v[i]), f[i] = i;
for (int i = 1; i <= m; i++)
{
int x, y;
scanf("%d%d%d", &e[i].x, &e[i].y, &e[i].w);
}
sort(e + 1, e + 1 + m);
for (int i = 1; i <= q; i++)
{
int x, k;
scanf("%d%d", &x, &k);
st[x].insert({k, i});
}
int p = 1;
for (int i = 1; i <= m; i++)
{
int x = e[i].x, y = e[i].y, w = e[i].w;
x = get(x);
y = get(y);
if (x == y)
continue;
// 从 x 出发的集合无法跨过 w
while (st[x].size() && (*st[x].begin()).first < w - v[x])
{
int id = st[x].begin()->second;
rs[id] = v[x] + st[x].begin()->first;
st[x].erase(st[x].begin());
}
while (st[y].size() && (*st[y].begin()).first < w - v[y])
{
int id = st[y].begin()->second;
rs[id] = v[y] + st[y].begin()->first;
st[y].erase(st[y].begin());
}
// 启发式合并，从小的集合合并到大的集合中
if (st[x].size() > st[y].size())
swap(x, y);
while (st[x].size())
{
st[y].insert(*st[x].begin());
st[x].erase(st[x].begin());
}
f[x] = y;
v[y] += v[x];
}
// 还有一些询问留在最后处理
for (int i = 1; i <= n; i++)
{
int x = get(i);
for (auto &t : st[x])
{
rs[t.second] = v[x] + t.first;
}
st[x].clear();
}
for (int i = 1; i <= q; i++)
{
printf("%d\n", rs[i]);
}
}
I Steadily Growing Steam
\(n\) 个卡牌，有价值 \(v_i\) 和点数 \(t_i\) ，你需要从中选出两组卡牌使得其点数和相等，然后最大化这两组的价值和。另外你可以选择不超过 \(k\) 个不同的卡牌，使得其 \(t_i\) 变成 \(2t_i\)。
\(k \le n \le 100, t_i\le 13, |v_i|\le 10^9\)。
考虑背包，我们仅关心这两组的点数和之差，所以可以把这个当做背包体积，如果第 \(i\) 个卡牌放入第一个集合，体积增加 \(t_i\)，否则体积减少 \(t_i\)，最后只需要取体积为 0 时候的答案即可。
另外还有一个体积是使卡牌点数翻倍的次数，所以状态可以定义为 \(d[i][j][w]\)，表示前 \(i\) 张卡牌，翻转恰好 \(j\) 次，两个集合体积差为 \(w\) 时的最大价值和。那么转移方程有：
此时，时间复杂度 \(O(n^3t_{max})\)，其中 \(t_{max} = 26\) 。注意到空间复杂度也是 \(O(n^3t_{max})\)，显然需要滚动数组优化。
#include<bits/stdc++.h>
using namespace std;
#define rep(i,j,k) for(int i=int(j);i<=int(k);i++)
#define per(i,j,k) for(int i=int(j);i>=int(k);i--)
typedef long long ll;
const int N = 105, M = 2605;
int n, k, v[N], t[N], T = 1300;
ll d[2][N][M];
/*
t_max = 26, 总和是 2600，但两个集合的差最多只需要维护 [-1300,1300] 即可，因为差距更大的话最终不会回到 0
数组访问下标不能为负数，所以加一个偏移量 T 即可。
*/
int main(){
scanf("%d%d", &n, &k);
rep(i,1,n) scanf("%d%d", &v[i], &t[i]);
memset(d, 0xcf, sizeof d); // v[i] 范围是 [-1e9,1e9]，所以答案提前初始化为负无穷
d[0][0][T] = 0; // 一开始什么都不选，答案为 0
int z = 1; // 滚动数组的下标
for(int i=1;i<=n;i++){
memset(d[z], 0xcf, sizeof d[z]);
for(int j=0;j<=k;j++){
for(int w=-1300;w<=1300;w++){
for(int p=-2;p<=2;p++){ // 5 种物品，体积分别为 -2t[i],-t[i],0,t[i],2t[i]，对应的价值为 v[i],v[i],0,v[i],v[i]
int wt = w + p * t[i]; // 转移后的体积
if(wt < -1300 || wt > 1300) continue; // 超出范围就过滤掉
if(j > 0) { // j > 0 表示 5 种物品都可以考虑转移
// 转移代码简略了一些，第一个点是 abs(p) = 2 时，要从 j - 1转移；第二个点是 p != 0 时价值为 v[i]
d[z][j][wt+T] = max(d[z][j][wt+T], d[z^1][j - (abs(p) == 2)][w + T] + (p == 0 ? 0 : v[i]));
} else if(abs(p) <= 1) { // j = 0 只能考虑不加倍点数的转移
d[z][j][wt+T] = max(d[z][j][wt+T], d[z^1][j - (abs(p) == 2)][w + T] + (p == 0 ? 0 : v[i]));
}
}
}
}
z^=1;
}
ll res = 0;
// 状态定义为恰好翻倍 k 次的最大价值，所以要遍历所有的 [1,k]。
for(int i=0;i<=k;i++) res = max(res, d[n&1][i][T]);
printf("%lld\n", res);
}
J Two Binary Strings Problem
给出两个长度为 \(n(n\le 50000)\) 的 01 串 \(A,B\)，对于每一个 \(1\le k\le n\)，遍历对于所有的 \(1\le i \le n\)，定义 $C_i $ 为集合 \(\{A_{max(i-k+1,1)},...,A_{i-1},A_i\}\) 里面的众数（题目定义：如果 1 的个数严格多于一半，就是 1，否则是 0），如果每个 \(C_i = B_i\) 成立，那么就输出 1，否则输出 0。
题意很绕，举个例子：
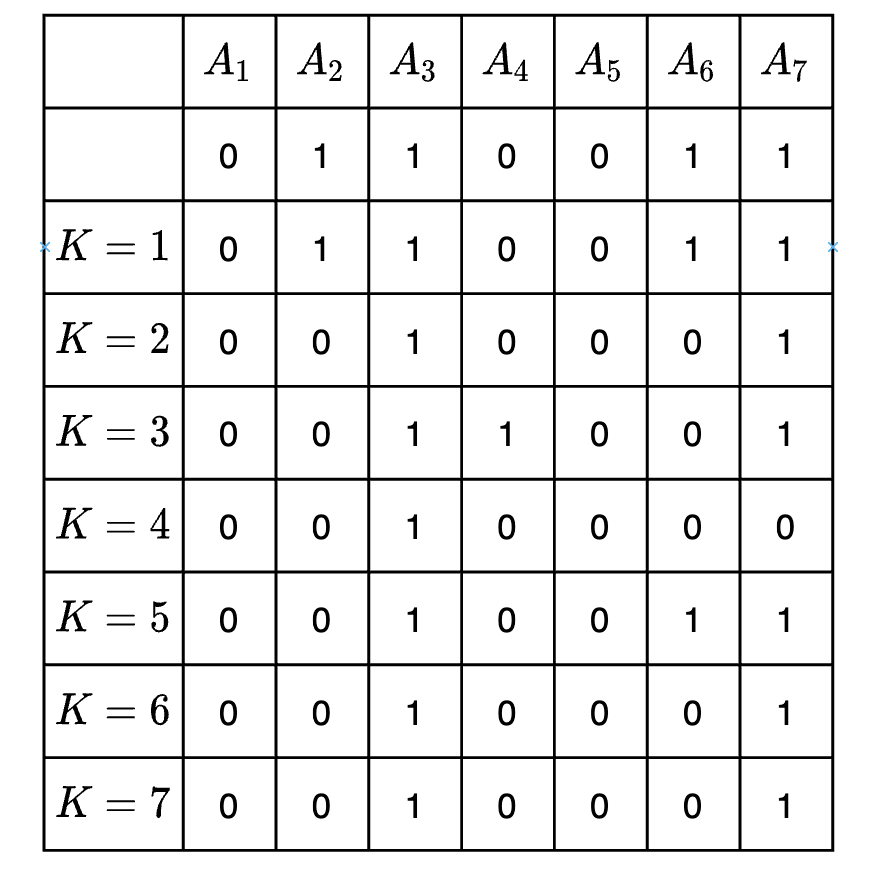
\(A = 0110011\)，对于每个 \(K\)，可以将其转换成每一行上的 \(C\)，如果第 \(i\) 行上的 \(C=B\)，那么就输出 1，否则输出 0。
这题需要找规律递推，不妨借助这个图，去发现一些规律。
考虑对于每个 \(A_i\)，一次性求出 \(k\in [1,n]\) 时的所有 \(C_i\)。可以用 bitset 快速维护，并且利用之前的答案递推。
当前枚举 \(i\)，试图找到一个最近的 \(j\)，满足 \(A_{j+1},\cdots,A_i\) 中 0 和 1 的个数相同。考虑如果借助计算出的 \(n\) 个 \(C_j\) 去递推 \(n\) 个 \(C_i\)。
如果 \(A_i=1\)，那么当 \(k = 1,2,\cdots,i-j-1\) 时，\(C_i=1\)。因为这一段数字中，1的个数永远比 0 的个数多；当 \(k=i-j\) 时，\(C_i=0\)，因为此时 0 和 1 的个数恰好一样多。那么当 \(k=t>i-j\) 时，就可以使用 \(C_j\) 去递推了。原因在于每个位置，1 和 0 的大小关系是等同的。
递推例子：
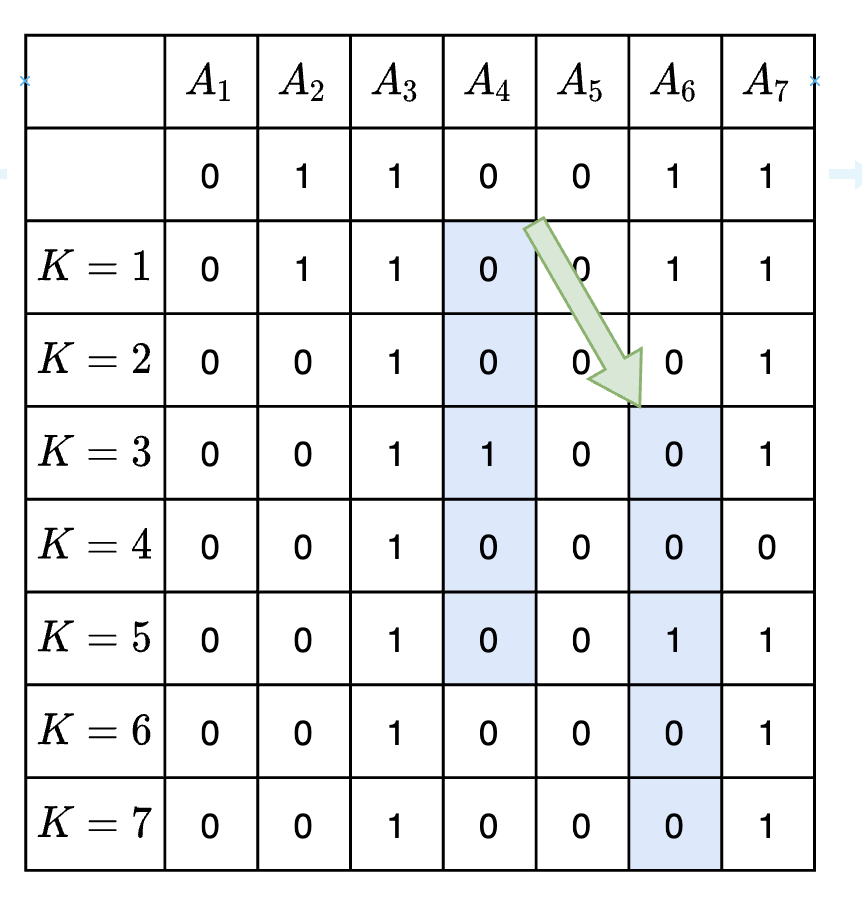
细节上如何递推：第 \(i\) 列的 \(n\) 个数字可以看做一个 \(n\) 位二进制（第 \(p\) 位对应 \(k=p+1\) 时的 \(C_i\)），使用 bitset 维护，叫做 \(f_i\)
找到上面描述的那个 \(j\)，如果找不到：
- 如果 \(A_i=1\)，那么 \(f_i\) 的所有 \(n\) 位都是 1
- 如果 \(A_i=1\)，那么 \(f_i\) 的所有 \(n\) 位都是 0
如果找到了 \(j\)：
- 如果 \(A_i = 1\)，那么 \(f_i\) 的 \(0\sim i-j-2\) 位都是 1（对应 \(k=1,\cdots,i-j-1\)），第 \(i-j-1\) 位是 0。然后 \(f_i = f_i | (f_{j}\ll (i-j))\)
- 如果 \(A_i=0\)，那么 \(f_i\) 的 \(0\sim i-j-1\) 位都是 0，然后 \(f_i = f_i|(f_j\ll (i-j))\)
最后要计算所有合法的 \(k\)，用一个长度为 \(n\) 的二进制数 \(st\) 表示合法状态，起初所有位上都是 1，遍历所有 \(i\)，只需要每次与\(f_i\) 中的合法状态做位与运算即可。当 \(B_i=1\) 时，\(f_i\) 中为 1 的位合法，否则 \(f_i\) 中为 0 的位合法。
其他详细情况可见代码。细节蛮多，可以考虑下标从 0 开始，会省去二进制数字中第 0 位的特殊处理。
#include<bits/stdc++.h>
using namespace std;
#define rep(i,j,k) for(int i=int(j);i<=int(k);i++)
#define per(i,j,k) for(int i=int(j);i>=int(k);i--)
typedef long long ll;
const int N = 50010;
int T, n;
char a[N], b[N];
bitset<N> c[N], cn, rs;
void solve(){
unordered_map<int,int> mp; mp[0] = -1;
int dis = 0;
// 先制作一个 0~n-1 位都是 1 的二进制数字
cn.reset(); rs.reset();
for(int i=0;i<n;i++) cn[i] = 1;
rs = cn; // 保存答案，也就是合法状态 st
for(int i=0;i<n;i++){
dis += (a[i] == '1' ? 1 : -1);
c[i].reset(); // c[i] 全部置为 0
if(mp.count(dis)) {
int j = mp[dis];
if(a[i] == '1') { // c[i] 的 0 ~ i-j-2 位都是1
c[i] |= cn >> (n - (i - j - 1));
}
if(j >= 0) // 如果 j = -1，不需要或运算
c[i] |= c[j] << (i - j);
} else { // 不存在 j
if(a[i] == '1') c[i] = cn;
}
if(c[i][i] == 1) { // 如果看不懂，思考上面的 C_3 的后缀 1
c[i] |= (cn >> i) << i;
}
mp[dis] = i;
if(b[i] == '1') {
rs &= ~(c[i] ^ cn);
} else {
rs &= ~c[i];
}
}
for(int i=0;i<n;i++) {
if(rs[i] == 1) putchar('1');
else putchar('0');
}
puts("");
}
int main(){
scanf("%d", &T);
while(T--){
scanf("%d", &n);
scanf("%s%s", a, b);
solve();
}
}
K Circle of Life
构造一个长度为 \(n\) 的 01 串，每一次变换的规则如下：
- 第 \(i\) 位如果为 1，那么变换后第 \(i+1\) 和第 \(i-1\) 位为 1。最左边和最右边的溢出不需要管。
- 如果\(i\) 和\(i+2\) 位都为 1，那么这两个 1 会在 \(i+1\) 发生冲撞抵消，第 \(i+1\) 位变换后为 0。
- 如果 \(i\) 和 \(i+1\) 位都为 1，那么变换后 \(i\) 和 \(i+1\) 位也为 0。
要求变换前与变换后，串内必须有 1，并且你需要保证构造出的串，可以在 \(2n\) 次变换内，出现两个完全相同的串。
打表找规律即可。附打表代码：
#include<bits/stdc++.h>
using namespace std;
#define rep(i,j,k) for(int i=int(j);i<=int(k);i++)
#define per(i,j,k) for(int i=int(j);i>=int(k);i--)
typedef long long ll;
bool check(string s){
for(auto &c : s) if(c == '1') return true;
return false;
}
bool ok(string s) {
unordered_map<string,int> mp;
int cnt = 0;
while(check(s)) { // 每次变换需要保证二进制串中有 1
mp[s] = 1;
string t = s;
for(int i=0;i<s.length();i++){ // 遍历 s 的每一位
t[i] = '0';
int flag = i > 0 ? s[i-1] == '1' : false; // 查看 s[i-1] 是否为 1
int flag2 = i + 1 < s.length() ? s[i + 1] == '1' : false; // 查看 s[i+1] 是否为 1
int flag3 = s[i] == '1'; // 查看 s[i] 是否为 1
// t[i] 为 1 当且仅当 (s[i-1] 或 s[i+1] 其中有一个是 1 并且 s[i] 为 0)
if(flag + flag2 + flag3 == 1 && flag3 == 0) t[i] = '1';
}
if(mp[t]) return true; // 如果出现相同，则合法
s = t;
cnt ++;
if(cnt > 2 * s.length()) return false; // 如果变换次数超过上限，返回false
}
return false;
}
void solve(int n) {
cout << "group " << n << " : "<< endl;
for(int i=0;i<(1<<n);i++){ // 二进制枚举
string s = "";
for(int j=0;j<n;j++){
if(i >> j & 1) s += "1";
else s += "0";
}
if(ok(s)) {
cout << s << endl;
// break;
}
}
}
int main(){
int n; // 输入 n，找到长度为 n 的所有合法串
cin >> n;
solve(n);
}
打出表来之后，可以先观察长度为 2、3、4、5、6、7、8 等长度的串。发现可以使用 1001 作为一个单元去构造后面延长的循环串。
AC代码：
#include <bits/stdc++.h>
using namespace std;
#define rep(i, j, k) for (int i = int(j); i <= int(k); i++)
#define per(i, j, k) for (int i = int(j); i >= int(k); i--)
typedef long long ll;
int n;
string s[] = {"0", "0", "01", "", "1001", "10001", "011001", "0101001"};
void solve() {
cin >> n;
if (n == 3) {
puts("Unlucky");
} else {
if (n <= 7) {
cout << s[n] << endl;
} else {
int cnt = 0;
if (n % 4 == 0) {
cnt = n / 4;
} else if (n % 4 == 1) {
cout << s[5];
cnt = n / 4 - 1;
} else if (n % 4 == 2) {
cout << s[2];
cnt = n / 4;
} else {
cout << s[7];
cnt = n / 4 - 1;
}
for (int i = 0; i < cnt; i++)
cout << "1001";
cout << endl;
}
}
}
int main() { solve(); }
