HDU-4773 Problem of Apollonius （圆的反演）

参考：

知识点：圆的反演

反演中心 O，半径R，若 P 与 P' 满足：

点 \(P'\) 在射线\(\overrightarrow {OP}\)上
\(|OP|\cdot |OP'| = R^2\)

则 P' 是 P 关于圆 O 的反演

性质：

圆外反演到圆内，反之亦然，圆O上的点反演为其自身
不过点O的圆A，其反演的圆也不过点O
过O的圆A，其反演图像是过点O的直线
两个圆相切，则他们的反演图像也相切

反演公式：

记圆O半径\(R\),圆心坐标\((x_0,y_0)\)

圆A半径\(r_1\)，圆心坐标\((x_1, y_1)\)

则圆A关于圆O的反演：圆B的半径为：

\[r_2={1\over 2}R^2({1\over |OA|-r_1}-{1\over |OA|+r_1}) \]

另外圆心B与O的距离\(|OB|\) 有：

\[r_2={1\over 2}R^2({1\over |OA|-r_1}+{1\over |OA|+r_1}) \]

圆心B坐标：

\[x_2 = x_0 + {|OB|\over|OA|} (x1 - x_0) \\ y_2 = y_0 + {|OB|\over|OA|} (y1 - y_0) \]

//圆 c 关于 p 反演所得到的圆
circle inverse(circle c, Point p, db R){
    db OA = c.p.distance(p);
    db x = OA - c.r, y = OA + c.r;
    circle res;
    res.r = 0.5 * R * R * (1.0/x - 1.0/y);
    db OB = 0.5 * R * R * (1.0/x + 1.0/y);
    res.p = p + (c.p - p) * (OB/OA);
    return res;
}

// AB直线关于圆P反演
circle inverse_l2c(Point p, Point A, Point B, db R){
    circle res;
    Point q = lineprog(p, A, B); //p在AB上面的映射
    db dis = q.distance(p);
    res.r = R * R * 0.5 / dis;
    res.p = p + (q - p) / dis * res.r;
    return res;
}

回到这一题：

根据性质3可以知道，反演不改变相切的关系，所以关于圆P(半径随意定)，将两个圆反演，求出这两个圆的切线，然后再将切线反演后，得到与原本的两个圆相外切的两个圆

将两个圆反演之后，这两个圆只需要求外公切线即可，并且这个外公切线，还需要满足一些条件才能被选做答案

首先为什么要求外公切线：

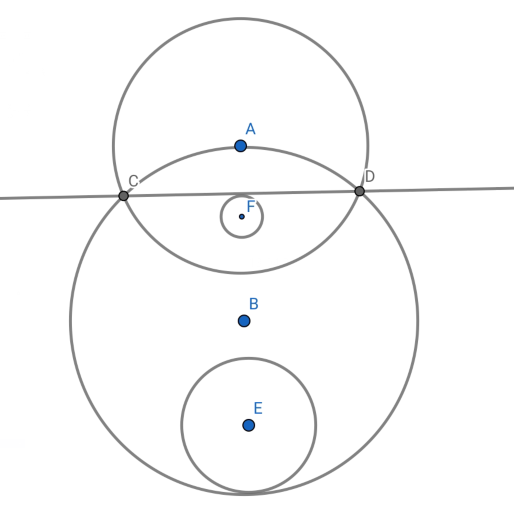
设点A在圆B上

圆B关于圆A反演得到直线CD，现在圆E是内切于圆B中，关于圆A反演得到圆F，可以发现圆心F，与点A是在CD异侧的，其实这个现象不难解释，从圆反演的定义即可推导出。

那么相反的，如果一个圆外切于圆B，那么关于圆A的反演得到的圆的圆心，一定与A在CD的同侧。

这样就解释了为什么题目中的两个圆反演之后需要求外公切线，另外，这条外公切线还必须使得点A和那两个反演圆的圆心在同侧

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int inf = 0x3f3f3f3f;
#define dbg(x...) do { cout << "\033[32;1m" << #x <<" -> "; err(x); } while (0)
void err() { cout << "\033[39;0m" << endl; }
template<class T, class... Ts> void err(const T& arg,const Ts&... args) { cout << arg << " "; err(args...); }
typedef double db;
const db eps = 1e-8;
const db pi = acos(-1);
int sgn(db x){
    if(fabs(x) < eps)return 0;
    if(x > 0) return 1;
    else return -1;
}
inline db sqr(db x){return x * x; }
struct Point{
    db x, y;
    Point(){}
    Point(db x, db y):x(x),y(y){}
    void input(){
        scanf("%lf%lf", &x, &y);
    }
    Point operator - (const Point &b){
        return Point(x - b.x, y - b.y);
    }
    db operator ^ (const Point b){
        return x * b.y - y * b.x;
    }
    db operator * (const Point b){
        return x * b.x + y * b.y;
    }
    Point operator + (const Point &b){
        return Point(x + b.x, y + b.y);
    }
    db distance(const Point &b){
        return hypot(x-b.x, y-b.y);
    }
    Point operator *(const db &k)const{
        return Point(x * k, y * k);
    }
    Point operator /(const db &k)const{
        return Point(x / k, y / k);
    }
    Point rotleft(){
        return Point(-y, x);
    }
    db len2(){
        return x * x + y * y;
    }
}p, a[10], b[10];
// p 在 AB 的投影
Point lineprog(Point p, Point A, Point B){
    return A + ( ( (B-A) * ((B-A) * (p-A)) ) / (B-A).len2());
}
struct circle{
    Point p;
    db r;
    circle(){}
    circle(Point p, db r):p(p),r(r){}
    void input(){
        p.input();
        scanf("%lf", &r);
    }
    Point point(double a){
        return Point(p.x + cos(a) * r, p.y + sin(a) * r);
    }
}c1, c2;
/*
getTangents 函数求出了所有的公切线，由于题目保证了两个圆没有公共点，那么这两个点一定会有四条公切线，我们只需要前两条即外公切线。
*/
// a[i] 存放第 i 条公切线与 圆A 的交点
int getTangents(circle A, circle B, Point*a, Point *b){
    int cnt = 0;
    // 以A为半径更大的那个圆进行计算
    if(A.r < B.r) return getTangents(B, A, b, a);
    db d2 = (A.p-B.p).len2();  // 圆心距平方
    db rdiff = A.r - B.r;        // 半径差
    db rsum = A.r + B.r;        //半径和
    if(d2 < rdiff * rdiff) return 0;     // 情况1，内含,没有公切线
    Point AB = B.p - A.p;                // 向量AB，其模对应圆心距
    db base = atan2(AB.y, AB.x);        // 求出向量AB对应的极角
    if(d2 == 0 && A.r == B.r) return -1;// 情况3，两个圆重合，无限多切线
    if(d2 == rdiff * rdiff){             // 情况2，内切，有一条公切线
        a[cnt] = A.point(base);            
        b[cnt] = B.point(base);cnt++;
        return 1;
    }
    // 求外公切线
    db ang = acos((A.r - B.r) / sqrt(d2)); //求阿尔法
    // 两条外公切线， 此题所需要的公切线
    a[cnt] = A.point(base+ang); b[cnt] = B.point(base+ang); cnt++;
    a[cnt] = A.point(base-ang); b[cnt] = B.point(base-ang); cnt++;
    if(d2 == rsum * rsum){  // 情况5，外切，if里面求出内公切线
        a[cnt] = A.point(base); b[cnt] = B.point(pi+base); cnt++;
    }
    else if(d2 > rsum * rsum){    //情况6，相离，再求出内公切线
        db ang = acos((A.r + B.r) / sqrt(d2));
        a[cnt] = A.point(base + ang); b[cnt] = B.point(pi+base+ang);cnt++;
        a[cnt] = A.point(base - ang); b[cnt] = B.point(pi+base-ang);cnt++;
    }
    // 此时，d2 < rsum * rsum 代表情况 4 只有两条外公切线
    return cnt;
}
//圆 c 关于 p 反演所得到的圆
circle inverse(circle c, Point p, db R){
    db OA = c.p.distance(p);
    db x = OA - c.r, y = OA + c.r;
    circle res;
    res.r = 0.5 * R * R * (1.0/x - 1.0/y);
    db OB = 0.5 * R * R * (1.0/x + 1.0/y);
    res.p = p + (c.p - p) * (OB/OA);
    return res;
}
// 由直线反演得到圆
circle inverse_l2c(Point p, Point A, Point B, db R){
    circle res;
    Point q = lineprog(p, A, B);
    db dis = q.distance(p);
    res.r = R * R * 0.5 / dis;
    res.p = p + (q - p) / dis * res.r;
    return res;
}
// 判断点CD 是否在 AB 同侧
bool sameside(Point A, Point B, Point C, Point D){
    return sgn((C-A) ^ (B-A)) == sgn((D-A) ^ (B-A));
}
int main(){
    int T;scanf("%d", &T);
    while(T--){
        c1.input();
        c2.input();
        p.input();
        c1 = inverse(c1, p, 1.0);
        c2 = inverse(c2, p, 1.0);
        int cnt = getTangents(c1, c2, a, b);
        vector<circle> res;
        for(int i=0;i<2;i++){
            if(sameside(a[i], b[i], c1.p, c2.p) && sameside(a[i], b[i], c1.p, p)){
                circle t = inverse_l2c(p, a[i], b[i], 1.0);
                res.push_back(t);
            }
        }
        printf("%d\n",(int)res.size());
        for(int i=0;i<res.size();i++){
            circle t = res[i];
            printf("%.8f %.8f %.8f\n", t.p.x, t.p.y, t.r);
        }
    }
    return 0;
}

posted @ 2020-04-27 13:17 kpole 阅读(225) 评论(0) 编辑收藏举报

刷新页面返回顶部

今夕

HDU-4773 Problem of Apollonius （圆的反演）

公告