两个圆的公切线
两个圆的公切线
圆上任意一点拥有唯一的圆心角
struct circle{
Point p;
double r;
// 通过圆心角求圆上某一点
Point point(double a){
return Point(p.x + cos(a) * r, c.y + sin(a) * r);
}
}
根据两个圆的位置关系来确定情况
- 两个圆内含,没有公共点,没有公切线
- 两圆内切,有一个条公切线
- 两圆完全重合,有无数条公切线
- 两圆相交。有2条公切线
- 两圆外切,有3条公切线
- 两圆相离,有4条公切线
1 与 3 什么都不求,情况 2 可以直接求出直线AB的极角进而转换为圆心角来求切点,连接切点和圆心,旋转90度即可得到切线。
情况 4 有两条外公切线,求出圆心距 \(d\) 以及\(|AG|\) 即可求出 \(\alpha\) 的大小,根据 \(\vec{AB}\) 的极角进行旋转即可求出切点,进而得到切线
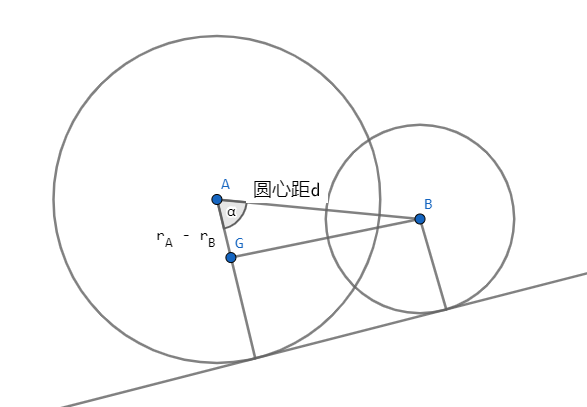
情况 5 的内切线类似情况2
情况 6 的外公切线与情况4完全一样
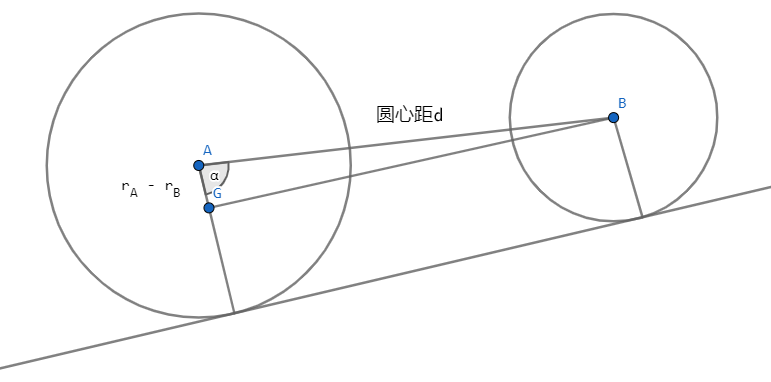
情况 6 的内切线也是先求出圆心角 \(\alpha\) ,如何求?\(\cos \alpha = \frac{A_r+B_r}{|AB|}\)
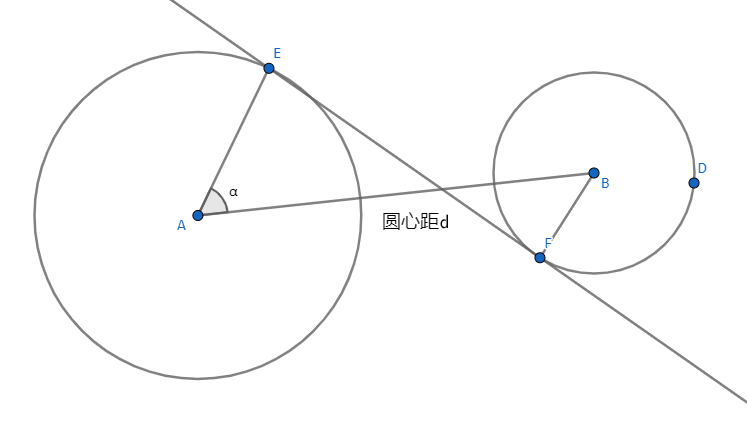
// a[i] 存放第 i 条公切线与 圆A 的交点
int getTangents(circle A, circle B, Point*a, Point *b){
int cnt = 0;
// 以A为半径更大的那个圆进行计算
if(A.r < B.r) return getTangents(B, A, b, a);
db d2 = (A.p-B.p).len2(); // 圆心距平方
db rdiff = A.r - B.r; // 半径差
db rsum = A.r + B.r; //半径和
if(d2 < rdiff * rdiff) return 0; // 情况1,内含,没有公切线
Vector AB = B.p - A.p; // 向量AB,其模对应圆心距
db base = atan2(AB.y, AB.x); // 求出向量AB对应的极角
if(d2 == 0 && A.r == B.r) return -1;// 情况3,两个圆重合,无限多切线
if(d2 == rdiff * rdiff){ // 情况2,内切,有一条公切线
a[cnt] = A.point(base);
b[cnt] = B.point(base);cnt++;
return 1;
}
// 求外公切线
db ang = acos((A.r - B.r) / sqrt(d2)); //求阿尔法
// 两条外公切线
a[cnt] = A.point(base+ang); b[cnt] = B.point(base+ang); cnt++;
a[cnt] = A.point(base-ang); b[cnt] = B.point(base-ang); cnt++;
if(d2 == rsum * rsum){ // 情况5,外切,if里面求出内公切线
a[cnt] = A.point(base); b[cnt] = B.point(pi+base); cnt++;
}
else if(d2 > rsum * rsum){ //情况6,相离,再求出内公切线
db ang = acos((A.r + B.r) / sqrt(d2));
a[cnt] = A.point(base + ang); b[cnt] = B.point(pi+base+ang);cnt++;
a[cnt] = A.point(base - ang); b[cnt] = B.point(pi+base-ang);cnt++;
}
// 此时,d2 < rsum * rsum 代表情况 4 只有两条外公切线
return cnt;
}
例题测试:https://onlinejudge.u-aizu.ac.jp/courses/library/4/CGL/7/CGL_7_G
注:转载请注明出处



 浙公网安备 33010602011771号
浙公网安备 33010602011771号