数字图像处理——图像增强

图像增强

图像增强的目的是：改善图像的视觉效果或使图像更适合于人或机器的分析处理

\[图像增强 \begin{cases} 空域法 \begin{cases} 点操作 \begin{cases} 直接灰度变换\\ 直方图修正 \end{cases}\\ 邻域操作 \begin{cases} 图像平滑\\ 图像锐化 \end{cases} \end{cases}\\ 频域法 \begin{cases} 低通滤波\\ 高通滤波 \end{cases} \end{cases} \]

点操作

直接灰度变换

\(g(x,y)=T[f(x,y)]\)

\(T\) => 灰度映射函数

坐标位置 \((x,y)\) 为 \(f\) 的自变量，表示当前灰度值，经过函数\(T\) 转变为\(g\)，
注意在T函数中\(f(x,y)\)为其自变量

直接灰度变换又可以分为：

• 线性变换
• 分段线性变换
• 非线性变换

线性变换 & 分段线性变换

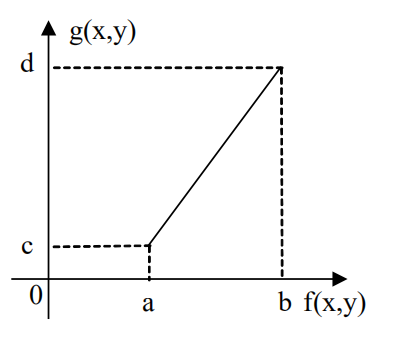
对于\(f(x,y)\)灰度范围为\([a,b]\)的部分，进行线性变换

\[g(x,y) = {d-c\over b-a}[f(x,y)-a]+c \]

我们可以用它来做什么？

举个简单的例子，我们可以很容易的通过调整灰度分布，使得图片白的部分更白，黑的部分更黑

void increase(Mat &inputImage, Mat& outputImage){
	outputImage = inputImage.clone();
	int rows = outputImage.rows;
	int cols = outputImage.rows;
	for (int i = 0; i < rows; i++){
		for (int j = 0; j < cols; j++){
			Vec3b & tmp = outputImage.at<Vec3b>(i, j);
			for (int k = 0; k < 3; k++){
				if (tmp[k] < 48)
					tmp[k] = tmp[k] / 1.5;
				else if (tmp[k] > 191)
					tmp[k] = (tmp[k] - 192) * 0.5 + 223;
				else tmp[k] = (tmp[k] - 38) * 1.33;
			}
		}
	}

效果图：

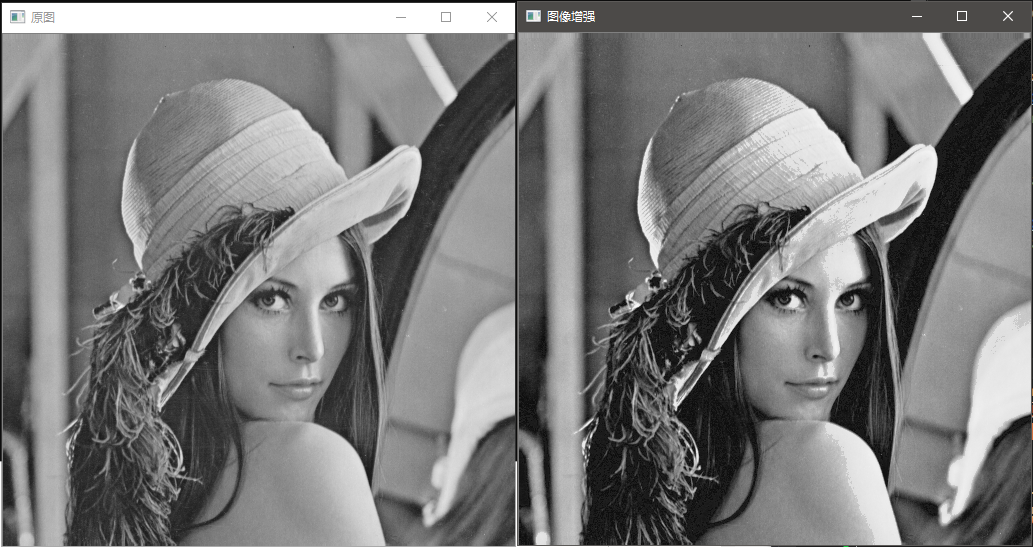
非线性灰度变换

\[g(x,y)=clog_{10}[1+f(x,y)] \]

直方图

在数字图像处理中，直方图是最简单并且最有用的工具

灰度直方图是灰度级的函数，描述的是图像中该灰度级的像素个数

横坐标表示灰度级，纵坐标表示图像中该灰度级出现的像素个数

数据表示：

变量	含义
n	图像的像素总数
L	灰度级的个数
\(r_k\)	第 k 个灰度级
\(n_k\)	第 k 个灰度级的像素数
\(p_r(r_k)\)	该灰度级出现的频率

则 归一化形式：

\[p_r(r_k) = {n_k\over n},~k = 0,1,2,\cdots,L-1 \]

公式利于归纳但是不利于理解，我们举个例子说明：

原始图像数据（每个位置上面的数字表示灰度级）

1	2	3	4	5	6
6	4	3	2	2	1
1	6	6	4	6	6
3	4	5	6	6	6
1	4	6	6	2	3
1	3	6	4	6	6

直方图

灰度系数	1	2	3	4	5	6
像素个数	5	4	5	6	2	14

归一化直方图数据

1/6	2/6	3/6	4/6	5/6	6/6
5/36	4/36	5/36	6/36	2/36	14/36

图像略

直方图性质

1. 直方图未反映某一灰度级像素所在位置，即丢失了位置信息
2. 一幅图像对应一个灰度直方图，但是不同的图像可能有相同的直方图
3. 灰度直方图具有可加性，整幅图像的直方图等于素有不重叠子区域的直方图之和

直方图用途

1. 反映图像的亮度、对比度、清晰度。用来判断一幅图像是否合理地利用了全部被允许的灰度级范围
2. 图像分割阈值选取，如果某图像的灰度直方图具有二峰性，那么这个图像的较亮区域与较暗区域可以较好分离，取谷底做为阈值点

直方图计算

先求出图像灰度级总数，然后遍历图像，对应像素点的灰度级的像素个数++，最后归一化即可

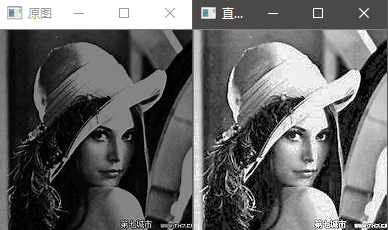
直方图均衡化

目的:将\(p_r(k_r)\) 修正为均匀分布形式，使动态范围增加，图像清晰度增加，对比度增加

方法：

1. 求出灰度直方图
2. 计算累积分布\(p'_s(s_k) = \sum_{j=0}^kp_r(r_j)\)
3. 计算新的灰度值\(s_k=int[(L-1)p's(s_k)+0.5]\)

\(r_k\)	\(n_k\)	\(p_r(r_k)\)	\(p'_s(s_k)\)	\(s_k\)	\(N'_k\)	\(p_s(s_k)\)
0	790	0.19	0.19	1	0	0
1	1023	0.25	0.44	3	790	0.19
2	850	0.21	0.65	5	0	0
3	656	0.16	0.81	6	1023	0.25
4	329	0.08	0.89	6	0	0
5	245	0.06	0.95	7	850	0.21
6	122	0.03	0.98	7	985	0.24
7	81	0.02	1.00	7	488	0.11

新的 \(N'_k\) 由上一级的\(n_k\) 而来

//可以直接调用opencv库写好的方法
void equalization(Mat &input, Mat &output){
	Mat imageRGB[3];
	split(input, imageRGB);
	for (int i = 0; i < 3;i++)
		equalizeHist(imageRGB[i], imageRGB[i]);
	merge(imageRGB, 3, output);
}