2019牛客暑期多校训练营（第九场） E All men are brothers

传送门

知识点：并查集+组合数学

并查集合并操作可以理解为使得两个集合的人互相成为朋友，也就是两个集合并在了一起，答案是要求从所有人中挑出四个互相不是朋友的四个人，比较基础的组合数学知识，但因为每个集合的大小预先不知，所以变得难以计算。

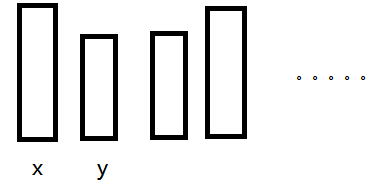
假设我们现在算出了合并前的答案，在合并x和y时，设 \(sz[x]\) 为\(x\)所在集合的集合大小，\(sz[y]\) 同理。考虑这两个集合对答案的贡献。有三种情况：

1. 从x所在集合中取一个人，然后再从其他非y集合中挑选出三个互不在同一集合的人
2. 从y所在集合中取一个人，然后再从其他非x集合中挑选出三个互不在同一集合的人
3. 从x,y所在集合中各取一个人，然后再从其他集合中挑选出两个互不在同一集合的人

考虑合并之后

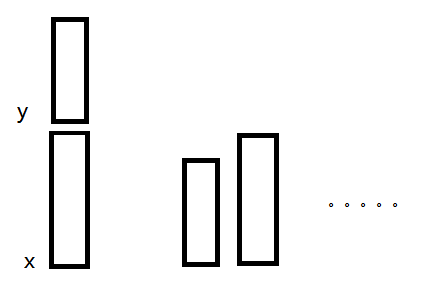
可以发现合并之后x和y在同一集合，仔细观察上面说到的情况1、2，它们对答案的贡献并没有因为合并操作而改变。只有情况3，在合并之后，该贡献被消灭，所以要用上一次的答案减去这个情况，就是合并之后的答案。

该怎么计算？情况3的答案等同于从非x,y的集合中挑两个集合并从这两个集合中各选一个人的情况总数。

举个例子，比如除去x,y所在的集合，剩下的集合的个数分别是

3 4 3 2

那么应该这么计算：

\((3*4 + 3*3 + 3 * 2) + (4*3+4*2) + (3*2)\)

等同于

\[((3+4+3+2) * (3+4+3+2) - (3^2 + 4^2+3^2+2^2)) \over 2 \]

总人数为n，sum为每个集合大小的平方和，那么情况3的总数为

\[num = {(n-sz[x]-sz[y])^2-(sum-sz[x]^2-sz[y]^2)\over 2} \]

然后 res -= num 更新答案即可

最后更新一下sum和 sz[x]或sz[y](取决于用哪个作为所在集合代表元素)

res初始化为\(C_n^4\)

由于n 是1e5,所以对n分情况讨论求\(C_n^4\)

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 100010;
ll n,m;
ll fa[N],sz[N];
int find(int x){
    return x == fa[x] ? x : fa[x] = find(fa[x]);
}
int main(){
    scanf("%lld%lld",&n,&m);
    for(int i=1;i<=n;i++)fa[i] = i,sz[i] = 1ll;
    if(n < 4){
        printf("0\n");
        while(m--){
            int x,y;scanf("%d%d",&x,&y);
            printf("0\n");
        }
        return 0;
    }
    ll res = 0;
    if(n % 4 == 0){
        res = n / 4 * (n-1) / 3 * (n-2) / 2 * (n-3);
    }
    else if(n % 4 == 1){
        res = n * (n-1) / 4 * (n-2) / 3 * (n-3) / 2;
    }
    else if(n % 4 == 2){
        res = n / 2 * (n-1) * (n-2) / 4 * (n-3) / 3;
    }
    else{
        res = n / 3 * (n-1)/2 * (n-2) / 1 * (n-3)/4;
    }
    printf("%lld\n",res);
    ll sum = n;
    while(m--){
        int x,y;
        scanf("%d%d",&x,&y);
        x = find(x);
        y = find(y);
        if(x == y){//如果已经在同一集合就不更新答案
            printf("%lld\n",res);
            continue;
        }
        sum -= sz[x] * sz[x];
        sum -= sz[y] * sz[y];
        res -= (sz[x] * sz[y]) * (((n - sz[x] - sz[y]) * (n - sz[x] - sz[y]) - sum)/2);
        fa[x] = y;
        sz[y] += sz[x];
        sum += sz[y] * sz[y];
        if(res < 0)res = 0;//res不能减成负数
        printf("%lld\n",res);
    }
    return 0;
}