2019牛客暑期多校训练营(第六场)C Palindrome Mouse (回文树+DFS)
题意
给一个字符串s,然后将s中所有本质不同回文子串放到一个集合S里面,问S中的两个元素\(a,b\)满足\(a\)是\(b\)的子串的个数。
分析
首先要会回文树(回文自动机,一种有限状态自动机)
然后可以很轻松的求出来S集合,我们拿出一个样例画出回文树看一下
abacaba
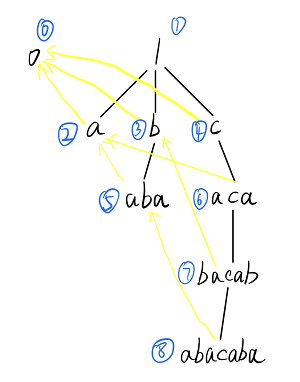
注: 上图中结点序号只是为了方便描述,与实际建树并不一定相同
0和1分别为偶数根和奇数根,黄边为fail边,总共有7个本质不同的回文串。
在计算答案时,我们从上到下统计,例如计算aba作为母串时的答案,那么子串有\(a\),\(b\)两个,
在计算\(bacab\)时,有\(aca, a, c, b,\) 四个。不难发现,如果把黄边也加入到整个树后,变成一张图,当我们计算某一结点(具体意义为一个回文串,比如7号节点)的答案时,我们要计算它的"祖先"(具有实际意义,即代表一个回文串,例如7号结点祖先为2,3,4,6)。
为了不重复记录,有必要标记我们已经考虑过的结点(也就是计算一个答案之后(比如7)再计算它的子节点的答案时(比如8),我们要把子节点的fail所指结点(比如5)和它自己(7)算进去),而在加这些新结点进行计算时要保证他们之前没有考虑过(比如5,但是7就不需要了,7肯定在之前没有考虑过)
但是不能只对5号结点标记访问,还需要对7标记已经访问,你可以看下面这个例子

在计算7号时,我们要把7号fail所指结点加到答案中去,但是按照我们之前的计算流程可以发现,i 已经在\(ehihe\)的祖先中了,所以不能重复添加。(因为这个坑wa了一发)
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 100010;
int T;
char s[N];
int n;
ll res;
namespace PAT{
const int SZ = 2e5+10;
int ch[SZ][26],fail[SZ],cnt[SZ],len[SZ],tot,last,dep[SZ];
int vis[SZ];
void init(int n){
for(int i=0;i<=n+10;i++){
fail[i] = cnt[i] = len[i] = vis[i] = dep[i] = 0;
for(int j=0;j<26;j++)ch[i][j] = 0;
}
s[0] = -1;fail[0] = 1;last = 0;
len[0] = 0;len[1] = -1,tot = 1;
dep[0] = dep[1] = 0;
}
inline int newnode(int x){
len[++tot] = x;return tot;
}
inline int getfail(int x,int n){
while(s[n-len[x]-1] != s[n])x = fail[x];
return x;
}
void create(char *s,int n){
s[0] = -1;
for(int i=1;i<=n;++i){
int t = s[i]- 'a';
int p = getfail(last,i);
if(!ch[p][t]){
int q = newnode(len[p]+2);
fail[q] = ch[getfail(fail[p],i)][t];
ch[p][t] = q;
}
++cnt[last = ch[p][t]];
}
}
int dfs(int p,ll tot){
//printf("%d %d\n",p,tot);
res += tot;
int isadd = (p!=0&&p!=1);//如果爸爸是0号和1号,没实际意义,不计入答案
vis[p] = 1;
for(int i=0;i<26;i++){
if(ch[p][i]){
int nxt = ch[p][i];
if(vis[fail[nxt]])
dfs(nxt,tot+isadd);
else{
vis[fail[nxt]] = 1;
int isaddfail = (fail[nxt]!=0 && fail[nxt] != 1);
dfs(nxt,tot+isadd+isaddfail);
vis[fail[nxt]] = 0;
}
}
}
vis[p] = 0;
}
void calc(){
dfs(0,0);
dfs(1,0);
}
}
int main(){
scanf("%d",&T);
int cas = 0;
while(T--){
scanf("%s",s+1);
n = strlen(s+1);
PAT::init(n);
PAT::create(s,n);
res = 0;
PAT::calc();
printf("Case #%d: %lld\n",++cas,res);
}
return 0;
}
注:转载请注明出处


