CF-1096C Polygon for the Angle
CF-1096C Polygon for the Angle
https://codeforces.com/contest/1096/problem/C
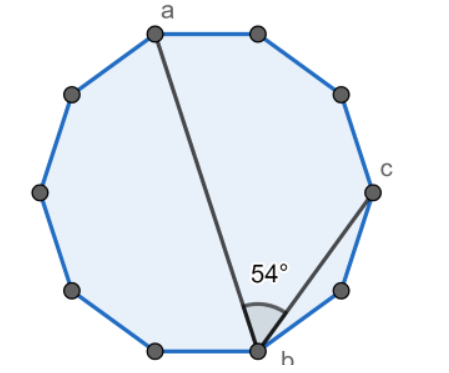
题意:给一个角度ang(1<=ang<=180) 然后输出如图所示规则的最小正n边形的边数
分析:abc三点构成一个三角形,而三角形内角的比例就对应于它们各自对应的那段边数比。如图,54度对应三份,剩下的分别对应五份和两份。
所以,对于任意一个角度ang,先求出g=gcd(ang,180),即每一边可以对应多少度,然后 n=180/g 即为正n边形的边数,wait wait!是不是有点太快了,别忘了我们的前提条件,我们是用三角形内角比例等于对应边数比得到的结论,我们要让它满足能够组成三角形这一条件,所以发现当 ang/180==(n-1)/n 时(想一想为什么是这样),就无法组成三角形(因为只剩下一份了,不够与ang组成三角形),这个时候只需将 n乘以2即可。
#include <bits/stdc++.h>
using namespace std;
int T,ang,n;
int main()
{
cin>>T;
while(T--)
{
cin >> ang;
int n = 180/__gcd(ang,180);
if(ang * n / 180 == n-1){
n*=2;
}
cout << n << endl;
}
}
注:转载请注明出处



