社团划分 Fast Unfolding&Fast newman（附代码和数据）

我来填坑啦qwq...

​ 大二的时候上离散课老师让实现社区划分算法，当时在网上找了一个类似的代码，但是有bug，自己调了调能用就交上去了，顺手在原博客下评论了一句。没想到两年后，我的评论炸了。。。。

竟然有21个回复，所以我回去翻了翻之前的数据备份，找到了源代码和数据，在此处分享一下，并填了两年前的坑（我真不是故意现在才填的）。原博客讲解fast unfolding链接在此

​ 第一个是大家都要的fast_unfolding算法，后面会贴所用数据的链接（之前的代码风格是真的烂）。

"""
    函数作用：加载数据，从指定文件中按行读取
    数据格式： Vertex1    Vertex2    Weight
               节点1       节点2      权重
    返回值：  保存节点的字典Vector_dict和保存边的字典edge_dict
"""


def loadData(filePath):
    # Step1： 打开文件，
    # 并初始化保存节点的Vector_dict和保存边的edge_dict
    f = open(filePath)
    vector_dict = {}
    edge_dict = {}
    # Step2：按行读取文件中信息，并根据特定格式对数据做出划分
    for line in f.readlines():
        # x.split()是根据括号内的内容分开
        # x.strip()是消除字符串头尾的指定字符串
        # 将每行数据划分为长度为3的List
        lines = line.strip().split("\t")
        # 因为做的是一个无向图，所以两个节点都要遍历
        for i in range(2):
            if lines[i] not in vector_dict:
                # 如果此节点不在保存节点的字典中
                # 将节点作为key放入字典，然后将value设为True
                vector_dict[lines[i]] = True
                # 初始化这个节点包含的边
                edge_list = []
            else:
                # 如果此节点在保存节点的字典中
                # 获取此节点之前的边集及边的权重
                edge_list = edge_dict[lines[i]]
            # 将边上的另一个节点及边的权重作为一个元素放入列表
            edge_list.append(lines[1-i]+":"+lines[2])
            # 更新字典中此节点包含的边
            edge_dict[lines[i]] = edge_list
    # Step3：返回包含节点的字典和包含边的字典
    return vector_dict, edge_dict


"""
    函数作用：计算模块度Q值，
    输入：划分好的社团节点集合vector_dict，边的集合edge_dict
    输出：模块度Q的值
    模块度计算的具体表达式如下(化简版)
    
    Q=∑_c〖[(∑In)/2m-〖((∑tot)/2m)〗^2]〗
    其中，∑In表示社区c内部的权重，
    ∑tot表示与社区c内部点连接的边的权重和
    原始模块度计算公式
    Q=(1/2m) * ∑_(i,j)〖[A_(i,j)-(k_i k_j)/2m]δ(c_i,c_j)〗
    其中，m表示网络中所有的权重和，A_(i,j)表示节点i到节点j之间边的权重
    m=1/2 ∑_(i,j)A_(i,j) 
    K_i表示和节点i连接的边的权重合。K_i=∑_j A_(i,j) 
    C_i表示顶点分配到的社区
    δ（c_i，c_j）用于判断顶点i和顶点j是否被划分在同一个社区中
"""


def modularity(vector_dict, edge_dict):
    Q = 0.0
    m = 0
    # Step1：对每一个点遍历，计算出权重合m
    for i in edge_dict.keys():
        edge_list = edge_dict[i]
        for j in range(len(edge_list)):
            l = edge_list[j].strip().split(":")
            m += float(l[1].strip())
    # Step2：找到每个社区的节点集合
    # Hint：vector_dict中
    # Key的值为节点，Value的值为社区号
    community_dict = {}
    for i in vector_dict.keys():
        if vector_dict[i] not in community_dict:
            community_list = []
        else:
            community_list = community_dict[vector_dict[i]]
        community_list.append(i)
        community_dict[vector_dict[i]] = community_list
    # Step3：计算∑In和∑tot
    # Hint：利用刚刚划分好的社区字典community_list
    # 对每个社区i分别计算∑In和∑tot
    for i in community_dict.keys():
        sum_in = 0.0
        sum_tot = 0.0
        # 找出来同一个社区的节点
        vector_list = community_dict[i]
        for j in range(len(vector_list)):
            # vector_list[j]含有的边集
            link_list = edge_dict[vector_list[j]]
            tmp_dict = {}
            for link_mem in link_list:
                l = link_mem.strip().split(":")
                # 先把边的另一个点放进去，值是权重
                tmp_dict[l[0]] = l[1]
            for k in range(0, len(vector_list)):
                if vector_list[k] in tmp_dict:
                    sum_in += float(tmp_dict[vector_list[k]])
        # 由于一条边储存了两次，所以计算的值也是实际的2倍
        # sum_tot计算较为简单，直接将点对应边的权重加和即可
        for vec in vector_list:
            link_list = edge_dict[vec]
            for i in link_list:
                l = i.strip().split(":")
                sum_tot += float(l[1])
        Q += ((sum_in / m) - (sum_tot/m)*(sum_tot/m))
    # Step4：将计算的Q值返回
    return Q


"""
    函数作用：更改社区归属，迭代每次结果，找到最大模块度的最大值
    输入：当前社区划分状态vector_dict，含有边的字典edge_dict及当前Q值
    输出：Q值最佳时的社区划分状态以及此时的模块度的值
"""


def change_community(vector_dict, edge_dict, Q):
    # Step1：初始化临时社区划分
    vector_tmp_dict = {}
    for key in vector_dict:
        vector_tmp_dict[key] = vector_dict[key]
    # Step2：遍历社团划分方式
    # Hint：如果两个节点之间有一条边，尝试将他们归为同一个社区
    # 然后计算模块度，若模块度变大，保留此次划分；若模块度减小，忽略此次划分
    for key in vector_tmp_dict.keys():
        neighbor_vector_list = edge_dict[key]
        # 当前的边
        for vec in neighbor_vector_list:
            # ori_com是当前点所在的社区
            ori_com = vector_tmp_dict[key]
            vec_v = vec.strip().split(":")
            if ori_com != vector_tmp_dict[vec_v[0]]:
                vector_tmp_dict[key] = vector_tmp_dict[vec_v[0]]
                Q_new = modularity(vector_tmp_dict, edge_dict)
                if (Q_new - Q) > 0:
                    Q = Q_new
                else:
                    vector_tmp_dict[key] = ori_com
    # Step3：返回新的社团划分以及新的模块度值
    return vector_tmp_dict, Q


"""
    函数作用：计算此时的社区数量，然后更新社区的名字(从0开始排列)
    输入：包含节点信息的社区划分的字典vector_dict
    输出：此时的社区数量
"""


def modify_community(vector_dict):
    # Step1：初始化计数器
    community_dict = {}
    community_num = 0
    # Step2：计算社区数量(第一个社区是0)
    for community_values in vector_dict.values():
        if community_values not in community_dict:
            community_dict[community_values] = community_num
            community_num += 1
    # Step3：更新社区名字
    for key in vector_dict.keys():
        vector_dict[key] = community_dict[vector_dict[key]]
    # Step4：返回社区数量
    return community_num


"""
    函数作用：重新构造社区网络，对原社区网络缩点
    函数使用条件：当前社区网络的模块度已达最大值
    输入：包含节点信息的社区划分的字典vector_dict，包含现有边的字典edge_dict
    当前社区数量community_num
    输出：新的包含节点信息的社区划分，新的边，原始社区节点划分
"""


def rebuild_graph(vector_dict, edge_dict, community_num):
    # Step1：初始化新的字典
    vector_new_dict = {}
    edge_new_dict = {}
    # cal the inner connection in every community
    community_dict = {}
    # Step2：根据原社区划分，将社区值设为community_dict的key
    # 将在同一个社区的节点作为对应key的value
    for key in vector_dict.keys():
        if vector_dict[key] not in community_dict:
            community_list = []
        else:
            community_list = community_dict[vector_dict[key]]
        community_list.append(key)
        community_dict[vector_dict[key]] = community_list
    # Step3：初始化新的包含社区划分的字典
    # 即将每一个社区中的人缩为一个点
    for key in community_dict.keys():
        vector_new_dict[str(key)] = str(key)
    # Step4.1：构造新的边，将每个社区内部边的权重作为新的边的权重
    # 然后令新边为一个社区的自环。一个社区缩为一个点后，产生一条由当前社区指向自己的边
    # 其权重为社区内部边权重的总和
    for i in community_dict.keys():
        sum_in = 0.0
        # 当前社区内的节点，计算社区内部的sum_in
        vector_list = community_dict[i]
        if '0' in vector_list:
            print(vector_list)
            print(i)
        for j in range(0,len(vector_list)):
            # 当前社区内某个节点包含的边
            link_list = edge_dict[vector_list[j]]
            tmp_dict = {}
            for link_mem in link_list:
                l = link_mem.strip().split(":")
                tmp_dict[l[0]] = l[1]
            for k in range(0, len(vector_list)):
                if vector_list[k] in tmp_dict:
                    sum_in += float(tmp_dict[vector_list[k]])
        # 初始化，每个节点都有指向自己的一条边
        inner_list = []
        inner_list.append(str(i) + ":" + str(sum_in))
        edge_new_dict[str(i)] = inner_list
    # Step4.2：计算两社区之间边的权重和，然后将权重和作为缩点后两社区边的权重
    community_list = list(community_dict.keys())
    for i in range(len(community_list)):
        for j in range(len(community_list)):
            if i != j:
                sum_outer = 0.0
                # 把两个社区的点都拿出来
                member_list_1 = community_dict[community_list[i]]
                member_list_2 = community_dict[community_list[j]]
                for i_1 in range(len(member_list_1)):
                    tmp_dict = {}
                    tmp_list = edge_dict[member_list_1[i_1]]
                    for k in range(len(tmp_list)):
                        tmp = tmp_list[k].strip().split(":")
                        tmp_dict[tmp[0]] = tmp[1]
                    for j_1 in range(len(member_list_2)):
                        if member_list_2[j_1] in tmp_dict:
                            sum_outer += float(tmp_dict[member_list_2[j_1]])
                # 如果i,j两个社区之间有联系，把和对应社区的联系设为新点之间的权重
                if sum_outer != 0:
                    inner_list = edge_new_dict[str(community_list[i])]
                    inner_list.append(str(j) + ":" + str(sum_outer))
                    edge_new_dict[str(community_list[i])] = inner_list
    # Step5：返回新构造的社区，边集，以及原始的社区节点划分
    return vector_new_dict, edge_new_dict, community_dict


"""
    函数作用：fast_unfolding的框架，调用各个子函数
    输入：原始的节点和原始的边
    输出：社区划分的过程以及最终的社区划分
"""


def fast_unfolding(vector_dict, edge_dict):
    # Step1：初始化原始节点，将每个节点划为一个社区
    for i in vector_dict.keys():
        vector_dict[i] = i
    # Step2：不断计算并迭代模块度，直至模块度达到当前划分的最大值
    Q = modularity(vector_dict, edge_dict)
    Q_new = 0.0
    while (Q_new != Q):
        Q_new = Q
        vector_dict, Q = change_community(vector_dict, edge_dict, Q)
    community_num = modify_community(vector_dict)
    # Step3：输出第一次迭代后的结果
    print("Q = ", Q)
    print(community_num)
    '''
    print("vector_dict.key : ", vector_dict.keys())
    print("vector_dict.value : ", vector_dict.values())
    '''
    # Step4：不断缩点，更新模块度的值
    Q_best = Q
    while True:
        # Step4.1：重建社区网络，缩点
        print("\n rebuild")
        vector_new_dict, edge_new_dict, community_dict = rebuild_graph(vector_dict, edge_dict, community_num)
        print("community_dict : ", community_dict)
        # Step4.2：重新计算模块度
        Q_new = 0.0
        while (Q_new != Q):
            Q_new = Q
            vector_new_dict, Q = change_community(vector_new_dict, edge_new_dict, Q)
        community_num = modify_community(vector_new_dict)
        # Step4.3：输出本次迭代的结果
        print("Q = ", Q)
        print("community_num : ", community_num)
        if (Q_best == Q):
            break
        Q_best = Q
        # Step4.4：
        vector_result = {}
        for key in community_dict.keys():
            value_of_vector = community_dict[key]
            for i in range(len(value_of_vector)):
                # 社区中的每个点为key，转化为社区
                vector_result[value_of_vector[i]] = str(vector_new_dict[str(key)])
        for key in vector_result.keys():
            vector_dict[key] = vector_result[key]
        # print("vector_dict.key : ", vector_dict.keys())
        # print("vector_dict.value : ", vector_dict.values())
    # Step5：输出最终解
    vector_result = {}
    for key in community_dict.keys():
        value_of_vector = community_dict[key]
        for i in range(len(value_of_vector)):
            vector_result[value_of_vector[i]] = str(vector_new_dict[str(key)])
    for key in vector_result.keys():
        vector_dict[key] = vector_result[key]
    print("Q_best : ", Q_best)
    print("vector_result.key : ", vector_dict.keys())
    print("vector_result.value : ", vector_dict.values())


if __name__ == "__main__":
    vector_dict, edge_dict=loadData("./data.txt")
    fast_unfolding(vector_dict, edge_dict)

代码中的data.txt点击此处从百度网盘获得（提取码gugh）。
算法运行结果如下图所示，进行了几次缩点，Q值在不断提升（squeezed text是python IDLE输出时缩进的，正常应该是输出的一堆结果）。

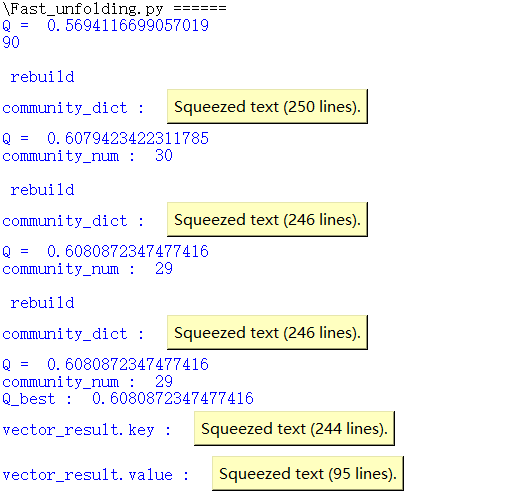
下面一个算法是fast newman，这个我忘了当时怎么搞的了，总之是社区划分算法，现在还能跑，里面有数据demo，也一并分享出来。

#-*- coding:utf-8 –*-

# 创建关系矩阵
def create_relation_matrix(List, n):
    adjacent_matrix = create_matrix(n, 0)
    for relation in List:
        adjacent_matrix[relation[0]][relation[1]] = 1
        adjacent_matrix[relation[1]][relation[0]] = 1
    return adjacent_matrix
# 输出列表
def printf(List):
    for x in List:
        print (x)
# 列表去重
def list_unique(List):
    new_list = []
    for id in List:
        if id not in new_list:
            new_list.append(id)
    return new_list
# 创建矩阵，number为矩阵一维个数，number为填充数字
def create_matrix(number, amount):
    matrix = []
    for i in range(0, number):
        tmp = []
        for j in range(0, number):
            tmp.append(amount)
        matrix.append(tmp)
    return matrix
# 查找包含该元素的所有位置
def find_index(List, node):
    return [i for i, j in enumerate(List) if j == node]

# 获取模块度
def get_modularity(node_list, node_club, club_list, node_matrix):
    uni = list_unique(club_list)
    # 更新社团位置
    for node in uni:
        idices = find_index(club_list, node)
        for i in idices:
            node_club[i] = uni.index(node)
    Q = 0
    m = sum([sum(node) for node in node_matrix])/2  # 网络的边的数目
    k = len(list_unique(node_club))  # 当前社团数目
    e = create_matrix(k, 0)  # 构造0矩阵
    for i in range(k):
        idx = find_index(node_club, i)
        labelsi = idx
        for j in range(k):
            idx = find_index(node_club, j)
            labelsj = idx
            for ii in labelsi:
                for jj in labelsj:
                    e[i][j] = e[i][j]+node_matrix[ii][jj]  # e[i][j]代表i社团与j社团之间有多少连接
    e = [[float(j)/(2*m) for j in i] for i in e]
    a = []
    for i in range(k):
        ai = sum(e[i])
        a.append(ai)
        Q = Q + e[i][i]-ai**2
    return Q, e, a, node_club
def fast_newman(node_list, List,n,divide_num):
    adjacent_matrix=create_relation_matrix(List, n)
    n = len(adjacent_matrix)
    max_id = n
    Z = []
    # 初始划分，node_list是节点标号，node_club是社团标号的变换，club_list是社团标号
    node_club = [0 for i in range(n)]
    club_list = [i for i in range(n)]
    step = 1
    while len(list_unique(club_list)) != 1:  # 计算满足条件的个数
        Q, e, a, node_club = get_modularity(node_list, node_club, club_list, adjacent_matrix)
        k = len(e)  # 社团数目
        DeltaQs = []
        DeltaQs_i = []
        DeltaQs_j = []
        for i in range(k):
            for j in range(k):
                if i != j:
                    DeltaQ = 2*(e[i][j]-a[i]*a[j])
                    DeltaQs.append(DeltaQ)
                    DeltaQs_i.append(i)
                    DeltaQs_j.append(j)
        maxDeltaQ = max(DeltaQs)  # 选择最大Q值的社团进行合并
        id_club = DeltaQs.index(maxDeltaQ)
        i = DeltaQs_i[id_club]
        j = DeltaQs_j[id_club]
        max_id = max_id + 1
        c_id1 = find_index(node_club, i)  # 获取社团i的标号
        c_id2 = find_index(node_club, j)  # 获取社团j的标号
        id1 = list_unique([club_list[item] for item in c_id1])  # 找到社团i的所有节点
        id2 = list_unique([club_list[item] for item in c_id2])  # 找到社团j的所有节点
        for item in c_id1:
            club_list[item] = max_id

        for item in c_id2:
            club_list[item] = max_id
        Z.append([id1, id2, len(c_id1+c_id2)])
        step = step + 1
        result_name = []
        result_index = []
        for item in list_unique(club_list):
            tmp = find_index(club_list, item)
            result_name.append([node_list[t] for t in tmp])
            result_index.append(tmp)
        if len(result_name) <= divide_num:
            break
    club_link=[]
    for item in List:
        if club_list[item[0]]!=club_list[item[1]]:
            club_link.append(item)

    return result_name,result_index,club_link
if __name__ == '__main__':
    List = [[0, 1], [1, 2], [1, 3], [3, 4], [3, 5], [3, 6], [4, 5], [1, 5]]
    node_list = ["node0", "node1", "node2", "node3", "node4", "node5", "node6"]
    print (fast_newman(node_list, List, 7, 3))

以上。