「2019纪中集训Day17」解题报告
T1、倾斜的线
平面上给定 \(n \ (n \leq 10 ^ 5)\) 个整点,选两个点使经过他们的直线斜率在数值上最接近 \(\frac{P}{Q} \ (1 \leq P,Q \leq 10 ^ 9)\);
以最简分数形式输出这个斜率,保证答案大于 \(0\),且不会有横坐标或纵坐标相等的点。
\(Sol\):
过每个点作一条斜率为 \(\frac{P}{Q}\) 的直线,把点按照直线的截距排序;
对于排序后的点,不难证明一个点的最优答案一定是它和与它相邻的某个点所在的直线。
时间复杂度 \(O(n \log_2 n)\)。
这道题好像不太能用整数做,直接 \(long \ double\) 即可。
\(Source\):
//#pragma GCC optimize(3,"Ofast","inline")
#include <cstdio>
#include <algorithm>
#include <cmath>
typedef long double db;
int in() {
int x = 0; char c = getchar(); bool f = 0;
while (c < '0' || c > '9')
f |= c == '-', c = getchar();
while (c >= '0' && c <= '9')
x = (x << 1) + (x << 3) + (c ^ 48), c = getchar();
return f ? -x : x;
}
template<typename T>inline void chk_min(T &_, T __) { _ = _ < __ ? _ : __; }
template<typename T>inline void chk_max(T &_, T __) { _ = _ > __ ? _ : __; }
const int N = 2e5 + 5;
const db eps = 1e-15;
struct node {
int x, y;
} a[N];
int n, P, Q;
inline bool cmp(const node &i, const node &j) {
return 1ll * P * i.x - 1ll * Q * i.y < 1ll * P * j.x - 1ll * Q * j.y;
}
int gcd(int _, int __) {
return __ ? gcd(__, _ % __) : _;
}
int main() {
//freopen("in", "r", stdin);
freopen("slope.in", "r", stdin);
freopen("slope.out", "w", stdout);
n = in(), P = in(), Q = in();
int d = gcd(P, Q); P /= d, Q /= d;
for (int i = 1; i <= n; ++i)
a[i].x = in(), a[i].y = in();
std::sort(a + 1, a + 1 + n, cmp);
int ansx = 1, ansy = 2;
db min = (db)(a[1].y - a[2].y) / (db)(a[1].x - a[2].x), base = (db)P / Q, M;
for (int i = 3; i <= n; ++i) {
M = (db)(a[i].y - a[i - 1].y) / (db)(a[i].x - a[i - 1].x);
if (fabs(fabs(M - base) - fabs(min - base)) < eps) {
if (M - base < eps)
ansx = i - 1, ansy = i;
} else if (fabs(M - base) - fabs(min - base) < eps) {
min = M, ansx = i - 1, ansy = i;
}
}
d = gcd(std::abs(a[ansx].y - a[ansy].y), std::abs(a[ansx].x - a[ansy].x));
printf("%d/%d\n", std::abs(a[ansx].y - a[ansy].y) / d, std::abs(a[ansx].x - a[ansy].x) / d);
return 0;
}
T2、最小值
给定一个长度为 \(n \ (n \leq 2 \times 10 ^ 5)\) 的整数序列 \(a\)。
定义一个区间 \([l,r]\) 的价值为 \(f( \min_{i = l} ^ {r} a_i )\), 其中: \(f(x) = Ax ^ 3 + B x ^ 2 + C x + D\)。
把序列 \(a\) 划分成若干区间,求最大价值和。
\(|f(x)| \leq 10 ^ {13}\),输入数据在 \(int\) 以内。
\(Sol\):
记 \(dp_i\) 表示序列前 \(i\) 位划分出的最大价值,显然有:
单调栈优化即可。
时间复杂度 \(O(n)\)。
\(Source\):
#include <cstdio>
#include <cstring>
#include <algorithm>
int in() {
int x = 0; char c = getchar(); bool f = 0;
while (c < '0' || c > '9')
f |= c == '-', c = getchar();
while (c >= '0' && c <= '9')
x = (x << 1) + (x << 3) + (c ^ 48), c = getchar();
return f ? -x : x;
}
template<typename T>inline void chk_min(T &_, T __) { _ = _ < __ ? _ : __; }
template<typename T>inline void chk_max(T &_, T __) { _ = _ > __ ? _ : __; }
const int N = 2e5 + 5;
int n, a[N], A, B, C, D;
std::pair<int, long long> sta[N];
int tp;
long long dp[N];
inline long long f(const int x) {
return 1ll * x * (1ll * x * (1ll * x * A + B) + C) + D;
}
int main() {
//freopen("in", "r", stdin);
freopen("min.in", "r", stdin);
freopen("min.out", "w", stdout);
n = in(), A = in(), B = in(), C = in(), D = in();
for (int i = 1; i <= n; ++i)
a[i] = in();
dp[0] = 0;
long long tmp;
for (int i = 1; i <= n; ++i) {
tmp = dp[i - 1];
while (tp && a[sta[tp].first] >= a[i])
chk_max(tmp, sta[tp--].second);
dp[i] = tmp + f(a[i]);
if (tp)
chk_max(dp[i], dp[sta[tp].first]);
sta[++tp] = std::make_pair(i, tmp);
}
printf("%lld\n", dp[n]);
return 0;
}
T3、安排
给定两个长度为 \(n \ (n \leq 2 ^ {12})\) 的排列 \(A,B\),现需通过以下操作将 \(A\) 变成 \(B\):
选择一个区间 \([l,r]\),交换这个区间里最大和最小的元素。
操作次数不能超过 \(345678\),输出一种方案。
\(Sol\):
老虎蒜头神仙题。
这个操作十分的不可控,要尽量让它可控,我们只能对一个有序区间进行操作。
不难发现,该操作 (交换) 是可逆的,因此可以将 \(A,B\) 分别排序,再按实际操作顺序输出。
排序的话,堆排、快排等算法显然不好用,考虑归并。
归并的关键在于如何合并两个排好序的区间,这里用到了快排的思想,如下图;
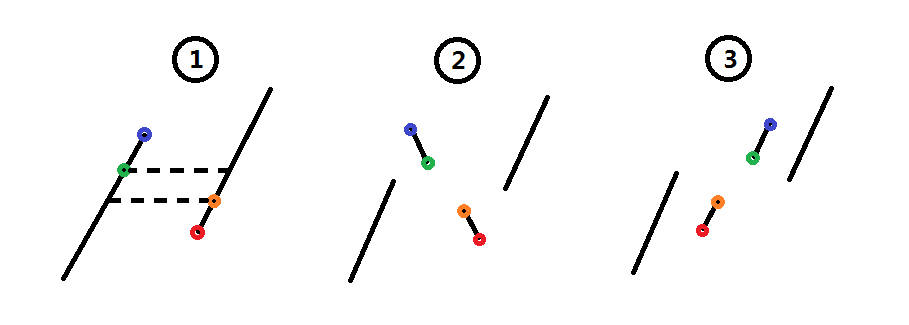
这样可以把两个区间分成两个新的部分,并且右边一定比左边大,递归即可。
这样合并一次的复杂度是 \(O(n \log_2 n)\)。
根据主定理,有 \(T(n) = 2T( \frac{n}{2} ) + n \log_2n = n \log_2 ^ 2 n\),总复杂度 \(O(n \log_2^2 n)\)。
我合并时写了随机化 (逃);
由于一些不可描述的边界问题,我也不知道这份代码对不对 (但它过了),欢迎 \(hack\)。
\(Source\):
//#pragma GCC optimize(3,"Ofast","inline")
#include <cstdio>
#include <algorithm>
#include <vector>
#include <cstdlib>
int in() {
int x = 0; char c = getchar(); bool f = 0;
while (c < '0' || c > '9')
f |= c == '-', c = getchar();
while (c >= '0' && c <= '9')
x = (x << 1) + (x << 3) + (c ^ 48), c = getchar();
return f ? -x : x;
}
template<typename T>inline void chk_min(T &_, T __) { _ = _ < __ ? _ : __; }
template<typename T>inline void chk_max(T &_, T __) { _ = _ > __ ? _ : __; }
const int N = 1e4 + 5;
int n, a[N], b[N];
std::vector<std::pair<int, int> > opt[2];
inline void swap(int &x, int &y) {
int t = x; x = y, y = t;
}
void rever(int l, int r, int k, int *f) {
while (l < r) {
swap(f[l], f[r]);
opt[k].push_back(std::make_pair(l++, r--));
}
}
void quick_merge(int l, int mid, int r, int k, int *f) {
if (l >= r)
return ;
if (l + 1 == r) {
if (f[l] > f[r])
rever(l, r, k, f);
return ;
}
if (f[mid] < f[mid + 1])
return ;
if (f[l] > f[r]) {
rever(l, mid, k, f);
rever(mid + 1, r, k, f);
rever(l, r, k, f);
return ;
}
int p1 = std::upper_bound(f + l, f + mid + 1, f[mid + 1]) - f;
int p2 = std::upper_bound(f + mid + 1, f + r + 1, f[mid]) - f - 1;
int p3, p4;
if (mid - p1 + 1 < p2 - mid) {
if (r - mid <= 1000) {
p4 = (mid + 1 + p2) >> 1;
} else {
p4 = rand() % (p2 - mid) + mid + 1;
}
p3 = std::upper_bound(f + p1, f + mid + 1, f[p4]) - f;
} else {
if (mid - p1 + 1 <= 1000) {
p3 = (p1 + mid) >> 1;
} else {
p3 = rand() % (mid - p1 + 1) + p1;
}
p4 = std::upper_bound(f + mid + 1, f + p2 + 1, f[p3]) - f - 1;
}
rever(p3, mid, k, f);
rever(mid + 1, p4, k, f);
rever(p3, p4, k, f);
quick_merge(l, p3 - 1, p3 - 1 + p4 - mid, k, f);
quick_merge(p4 - (mid - p3), p4, r, k, f);
}
void merge_sort(int l, int r, int k, int *f) {
if (l == r)
return ;
int mid = (l + r) >> 1;
merge_sort(l, mid, k, f), merge_sort(mid + 1, r, k, f);
quick_merge(l, mid, r, k, f);
//for (int i = 1; i <= n; ++i)
// printf("%d ", f[i]);
//puts("");
}
int main() {
//freopen("in", "r", stdin);
freopen("swap.in", "r", stdin);
freopen("swap.out", "w", stdout);
srand(40051326);
n = in();
for (int i = 1; i <= n; ++i)
a[i] = in();
for (int i = 1; i <= n; ++i)
b[i] = in();
merge_sort(1, n, 0, a);
merge_sort(1, n, 1, b);
printf("%d\n", (int)(opt[0].size() + opt[1].size()));
for (unsigned i = 0; i < opt[0].size(); ++i)
printf("%d %d\n", opt[0][i].first, opt[0][i].second);
std::reverse(opt[1].begin(), opt[1].end());
for (unsigned i = 0; i < opt[1].size(); ++i)
printf("%d %d\n", opt[1][i].first, opt[1][i].second);
return 0;
}

