zkw线段树学习笔记
zkw线段树学习笔记
今天模拟赛线段树被卡常了,由于我自带常数 \(buff\),所以学了下zkw线段树。
平常的线段树无论是修改还是查询,都是从根开始递归找到区间的,而zkw线段树直接从叶子结点开始操作。
建树
首先,我们需要把线段树补成一个堆形态的树,原序列在最后一层(最后一层的左右要留空,后面再讲为什么),这样一来,就可以轻松得出:原序列里第 \(x\) 个元素在线段树里的编号就是 \(x+2^k\) (其中 \(k\) 为线段树的深度,根节点深度为 \(0\) )
大概就是这样 :
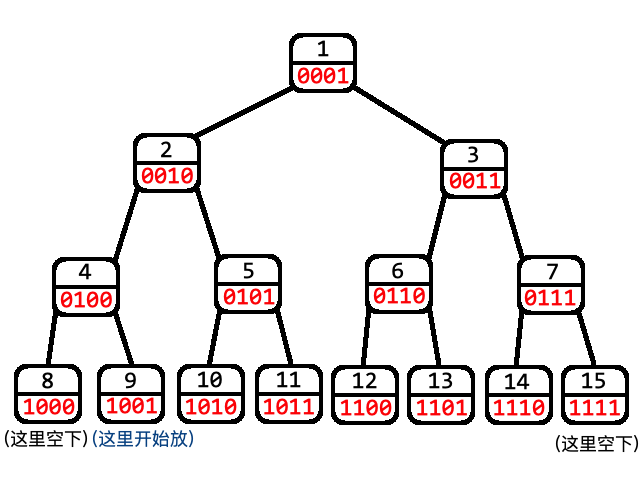
不难发现最后一层节点掐头去尾,就是原序列编号加上二进制最高位上的 \(1\)。
代码实现也非常简单:
segment_tree(const int n = 0) {
for (M = 1; M - 2 < n; M <<= 1); //M是最后一层的节点个数
for (int i = 1; i <= n; ++i)
t[i + M] = in();
for (int i = M - 1; i; --i)
t[i] = t[i << 1] + t[i << 1 | 1]; //合并子树信息
}
单点查询
直接查
单点修改
。。直接上代码:
void update(int p) {
for (p += M; p; p >>= 1) t[p] += k;
}
区间操作
若当前操作区间为 \([x,y]\),可以把它先转为开区间 \((x-1,y+1)\) (最后一层左右要留空的原因),设此开区间左右端点在线段树的编号为 \(l,r\)。
\(l, r\) 同时向它们的父亲节点跳,若 \(l\) 是它父亲的左儿子,则它父亲的右儿子被操作( \(r\) 与 \(l\) 对称),直到 \(l,r\) 的父亲相同。
可以配合图片理解:
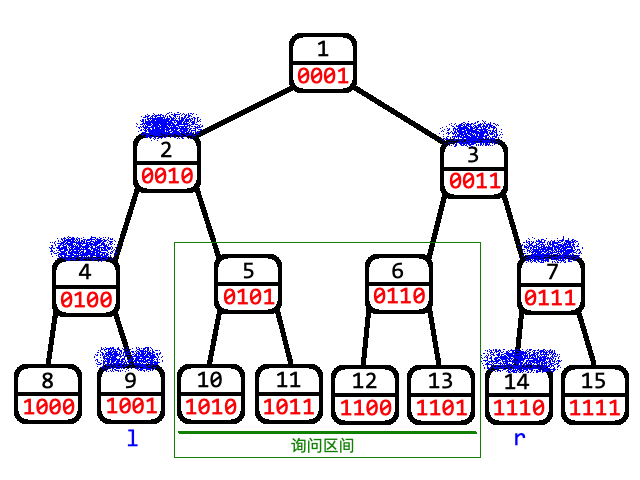
上图中:蓝色为 \(l,r\) 会跳到的点。因为查询区间为 \(l\) 右边和 \(r\) 左边组成的区间,当 \(l\) 为父亲的左儿子时,它父亲的右儿子一定在它左边( \(r\) 与 \(l\) 对称)。
区间修改、查询
这里以区间加法为例;
在普通的线段树中,一般用 \(lazy\) \(tag\) 来解决这个问题,zkw线段树同样可以,但从上向下操作、下放 \(lazy\) \(tag\) 等操作并不优雅 常数大。
可以采用标记永久化,随用随查,按zkw的说法——永久化的标记就是值。
考虑上文提到的区间操作的过程,自下向上走的过程中,根据遇到的标记来计算贡献。
具体实现细节可以看代码:
void modify(int l, int r, long long k) {
int lnum = 0, rnum = 0, now = 1;
//lnum 表示当前左端点走到的子树有多少个元素在修改区间内 (rnum与lnum对称)
//now 表示当前端点走到的这一层有多少个叶子节点
for (l = l + M - 1, r = r + M + 1; l ^ r ^ 1; l >>= 1, r >>= 1, now <<= 1) {
t[l] += k * lnum, t[r] += k * rnum;
if (~l & 1) t[l ^ 1] += k * now, add[l ^ 1] += k, lnum += now;
if (r & 1) t[r ^ 1] += k * now, add[r ^ 1] += k, rnum += now;
}
for (; l; l >>= 1, r >>= 1)
t[l] += k * lnum, t[r] += k * rnum;
}
long long query(int l, int r) {
int lnum = 0, rnum = 0, now = 1;
long long ret = 0;
for (l = l + M - 1, r = r + M + 1; l ^ r ^ 1; l >>= 1, r >>= 1, now <<= 1) {
if (add[l]) ret += add[l] * lnum;
if (add[r]) ret += add[r] * rnum;
if (~l & 1) ret += t[l ^ 1], lnum += now;
if (r & 1) ret += t[r ^ 1], rnum += now;
}
for (; l; l >>= 1, r >>= 1)
ret += add[l] * lnum, ret += add[r] * rnum;
return ret;
}
参考文献:《统计的力量》—— zkw


 浙公网安备 33010602011771号
浙公网安备 33010602011771号