kruskal重构树学习笔记
\(kruskal\) 重构树学习笔记
前言
\(8102IONCC\) 中考到了,本蒟蒻不会,所以学一下。
前置知识
\(kruskal\) 求最小(大)生成树,树上求 \(lca\)。
算法详解
\(kruskal\) 重构树可以解决瓶颈路问题(如:\(noip2013\) \(d1t3\) 货车运输,可以当做模板题来做,本文中也将此题作为例题);
我们来思考一下 \(kruskal\) 求最小(大)生成树的过程(后文中以最大生成树为例),大致过程可以概述为:将图中所有边从大到小排序,枚举,如果该边左右两端的点不在同一个联通块里就连起来,即:该边在最大生成树上。(其中联通块用 \(dsu\) 维护)
\(kruskal\) 重构树就是把最大生成树上的边建成树,实现过程:在 \(kruskal\) 算法进行过程中,对于每次要连接的两个联通块 \(A\) 和 \(B\),用一个新的节点当做 \(A\) \(B\) 在重构树中的父亲节点,并把新节点的点权设为连接联通块的边的边权,以此操作来代替连边操作,联通块同样用 \(dsu\) ,只不过是把 \(A\) \(B\) 并入新节点。
有一个比较明显的性质:最后建成的树一定是一个堆(大根堆小根堆视情况而定),因为边是按大小顺序枚举的,如果我表达不太清楚 \((QAQ)\) ,可以配合图解来学习。
具体来说,如果 \(kruskal\) 求最大生成树的过程是这样的:
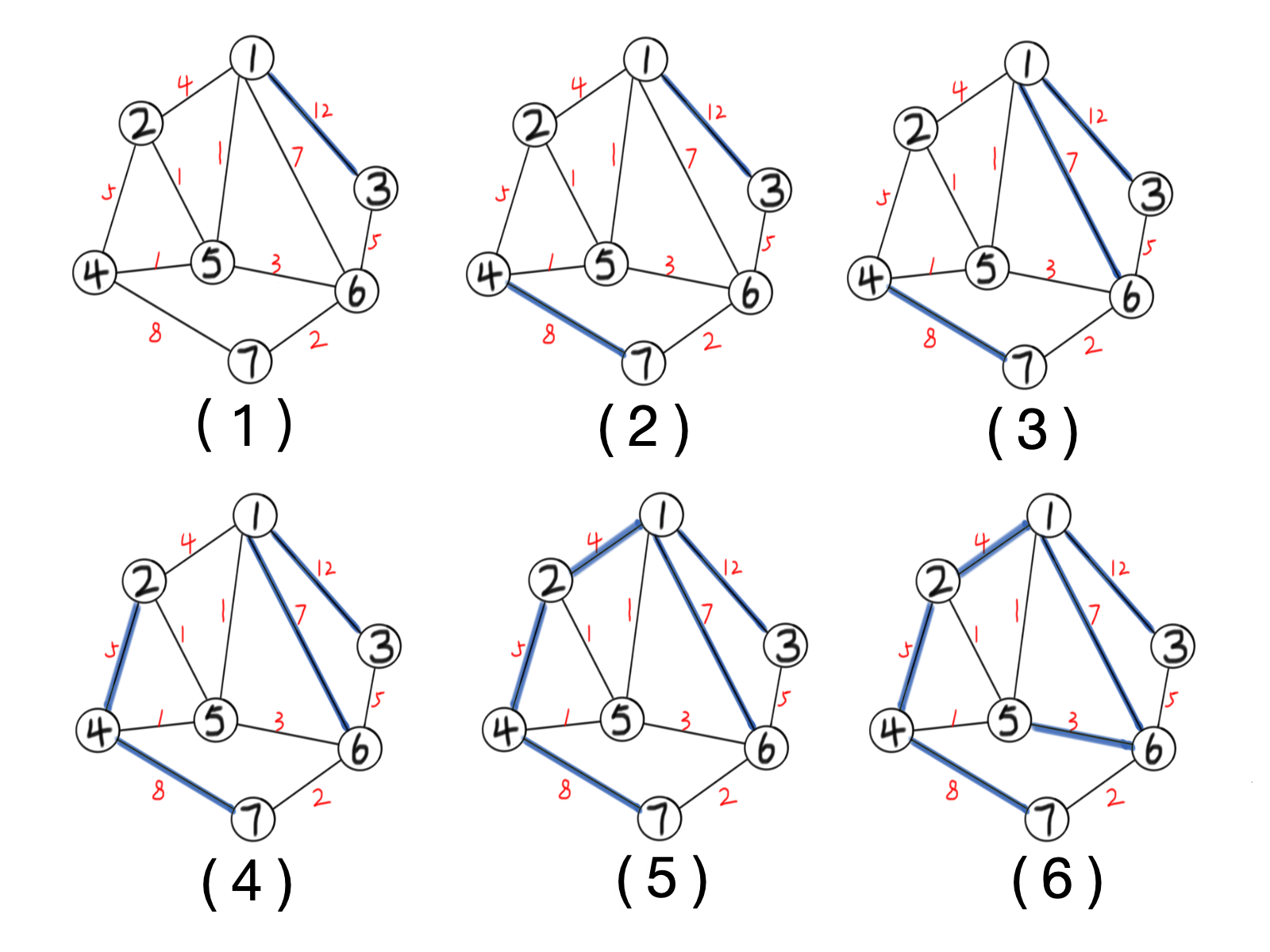
那么建树过程大概就是这样的(蓝色是新建节点):
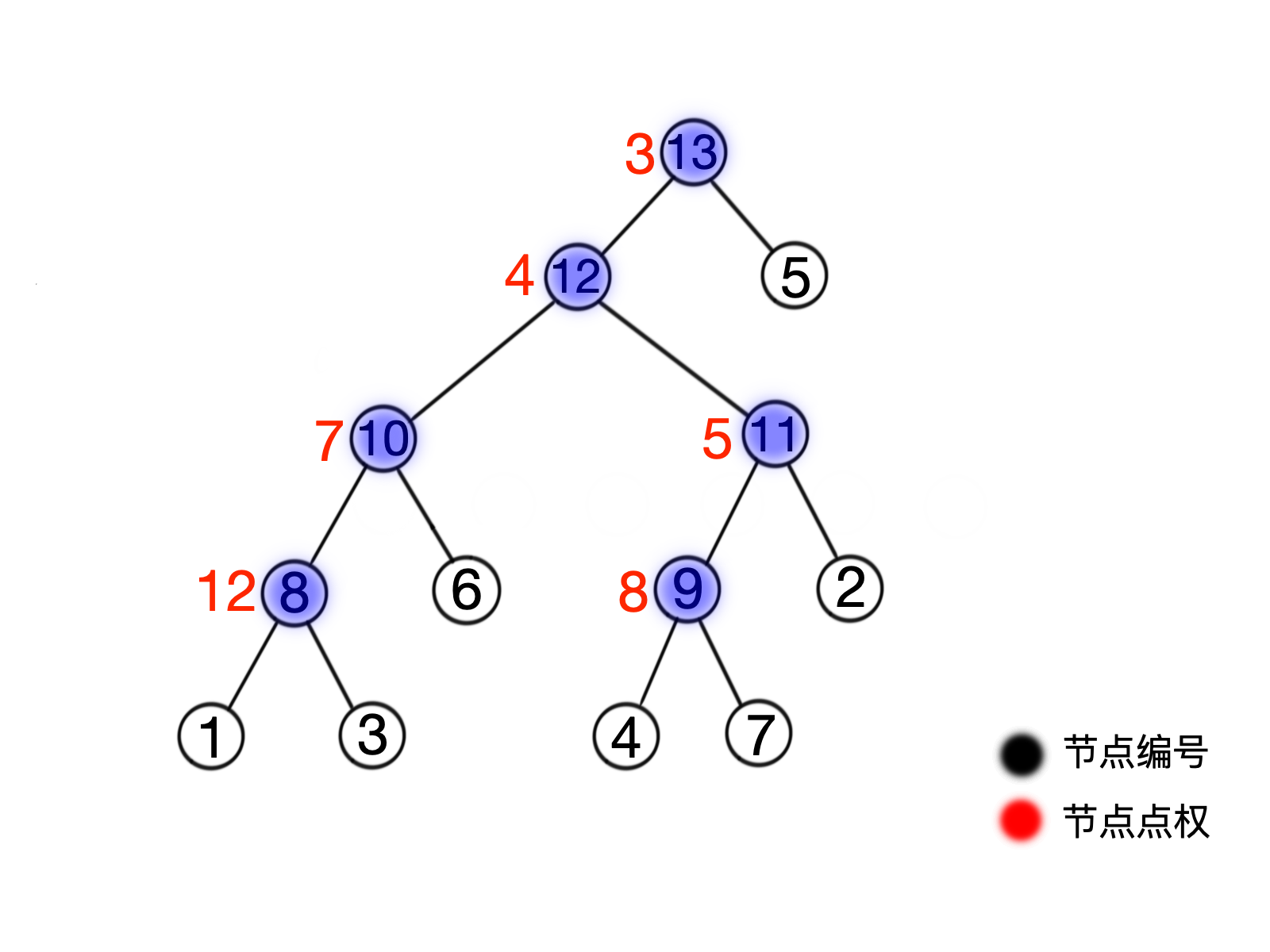
可以很直观地看到这真的是个堆,上文已经提到,不再赘述。
\(u,v\) 之间的瓶颈路,即:\(u,v\) 在重构树中的 \(lca\) 的点权。因为建树过程和 \(kruskal\) 同步进行,所以每个新建节点的点权是可以连接两棵子树所在联通块的最大边权,同时因为堆的性质 \(lca\) 是整颗以 \(lca\) 为根的子树中的最小值。(本人语文水平不及格,可以结合图片和 \(kruskal\) 的过程来理解)
\(p.s.\) 同样可以利用该性质证明瓶颈路一定在最大生成树上。
例题
\((noip2013\) \(d1t3)\)
这是一道模板题。
代码如下:
#include <cstdio>
#include <cstring>
#include <algorithm>
inline int in() {
int x=0;char c=getchar();bool f=false;
while(c<'0'||c>'9') f|=c=='-', c=getchar();
while(c>='0'&&c<='9') x=(x<<1)+(x<<3)+(c^48), c=getchar();
return f?-x:x;
}
const int N = 1e5+5, M = 5e5+5;
struct info {
int l, r, w;
inline bool operator < (const info &x) const {
return this->w > x.w;
}
}a[M+N];
int n, m, tot, fa[N<<1];
namespace kruskal_tree {
struct edge {
int next, to;
}e[N];
int head[N<<1], val[N<<1], cnt=1, size[N<<1], hson[N<<1], fro[N<<1], dep[N<<1];
inline void jb(int u, int v) {
e[++cnt]=(edge){head[u], v};
head[u]=cnt;
}
void dfs_h(int u) {
size[u]=1;
for(int i=head[u];i;i=e[i].next) {
int v=e[i].to;
fa[v]=u, size[u]+=size[v], dep[v]=dep[u]+1;
if(size[v]>size[hson[u]]) hson[u]=v;
dfs_h(v);
}
}
void dfs_f(int u, int father) {
fro[u]=father;
if(hson[u]) dfs_f(hson[u], father);
for(int i=head[u];i;i=e[i].next)
if(e[i].to!=hson[u]) dfs_f(e[i].to, e[i].to);
}
inline int lca(int u, int v) {
while(fro[u]!=fro[v]) {
if(dep[fro[u]]>dep[fro[v]]) std::swap(u, v);
v=fa[fro[v]];
}
return dep[u]<dep[v]?u:v;
}
inline void pre() {
dep[tot]=1;
dfs_h(tot); dfs_f(tot, tot);
}
inline int calc(int u, int v) {
return val[lca(u, v)];
}
}
int get_fa(int u) {
return fa[u]==u?u:fa[u]=get_fa(fa[u]);
}
inline void kruskal(info *e) {
tot=n;
std::sort(e+1, e+1+m);
for(int i=1;i<=n<<1;++i) fa[i]=i;
for(int i=1;i<=m;++i) {
int fx=get_fa(e[i].l), fy=get_fa(e[i].r);
if(fx==fy) continue;
fa[fx]=fa[fy]=++tot, kruskal_tree::val[tot]=e[i].w;
kruskal_tree::jb(tot, fx), kruskal_tree::jb(tot, fy);
}
kruskal_tree::pre();
}
int main() {
n=in(), m=in();
for(int i=1;i<=m;++i)
a[i].l=in(), a[i].r=in(), a[i].w=in();
for(int i=1;i<=n;++i)
a[++m]=(info){0, i, -1};
kruskal(a);
int q=in();
while(q--) {
int u=in(), v=in();
printf("%d\n", kruskal_tree::calc(u, v));
}
return 0;
}
\((noi2018\) \(d1t1)\)
一句话题解: \(dijsktra\) 预处理 \(1\) 为起点的最短路(权值为长度);建好 \(kruskal\) 重构树(海拔为权值),每次查询 \(v\) 时树上倍增一直跳就好了 \(qwq\)。
时间复杂度:\(\Theta \Big(T \times \big (mlogm+(q+n)logn \big) \Big)\)
代码如下:
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <queue>
typedef long long ll;
inline int in() {
int x=0;char c=getchar();bool f=false;
while(c<'0'||c>'9') f|=c=='-', c=getchar();
while(c>='0'&&c<='9') x=(x<<1)+(x<<3)+(c^48), c=getchar();
return f?-x:x;
}
const int N = 2e5+5, M = 4e5+5;
struct info {
int l, r, w;
friend inline bool operator < (const info &x, const info &y) {
return x.w > y.w;
}
}a[M];
struct edge {
int next, to, w;
}e[M<<1];
int head[N], cnt, n, m, tot, fa[M], d[N];
bool vis[N];
template<typename T>
inline void chk_min(T &_, T __) { _=_<__?_:__; }
namespace kt {
struct edge {
int next, to;
}e[N<<1];
int cnt=1, head[N<<1], min[N<<1], dep[N<<1], fa[19][N<<1], a[N<<1], L[19];
inline void jb(int u, int v) {
e[++cnt]=(edge){head[u], v};
head[u]=cnt;
}
void dfs(int u) {
for(int i=1;i<=18;++i)
if(dep[u]>L[i]) fa[i][u]=fa[i-1][fa[i-1][u]];
else break;
min[u]=2147483647;
if(1<=u&&u<=n) min[u]=d[u], a[u]=2147483647;
for(int i=head[u];i;i=e[i].next) {
int v=e[i].to;
dep[v]=dep[u]+1, fa[0][v]=u;
dfs(v);
chk_min(min[u], min[v]);
}
}
inline int query(int u, int s) {
for(int i=18;i>=0;--i)
if(dep[u]>L[i]&&a[fa[i][u]]>s)
u=fa[i][u];
return min[u];
}
}
inline void add_edge(int u, int v, int w) {
e[++cnt]=(edge){head[u], v, w}, head[u]=cnt;
e[++cnt]=(edge){head[v], u, w}, head[v]=cnt;
}
typedef std::pair <int, int> pii;
inline void dijkstra() {
std::priority_queue <pii> q;
memset(d, -1, sizeof(d));
memset(vis, false, sizeof(vis));
d[1]=0;
q.push(pii(0, 1));
while(!q.empty()) {
int u=q.top().second; q.pop();
if(vis[u]) continue;
vis[u]=true;
for(int i=head[u];i;i=e[i].next) {
int v=e[i].to;
if(d[u]+e[i].w<d[v]||d[v]==-1)
d[v]=d[u]+e[i].w, q.push(pii(-d[v], v));
}
}
}
int get_fa(int u) {
return fa[u]==u?u:fa[u]=get_fa(fa[u]);
}
inline void kruskal(info *e) {
tot=n;
for(int i=1;i<=n<<1;++i) fa[i]=i;
std::sort(e+1, e+1+m);
for(int i=1;i<=m;++i) {
int fx=get_fa(e[i].l), fy=get_fa(e[i].r);
if(fx==fy) continue;
++tot, kt::a[tot]=e[i].w;
kt::jb(tot, fx), kt::jb(tot, fy);
fa[fx]=fa[fy]=tot;
}
}
inline void init() {
cnt=kt::cnt=1;
memset(head, 0, sizeof(head));
memset(kt::head, 0, sizeof(kt::head));
}
int main() {
int T=in();
kt::L[0]=1;
for(int i=1;i<=18;++i) kt::L[i]=kt::L[i-1]<<1;
while(T--) {
init();
n=in(), m=in();
for(int i=1, u, v, l, h;i<=m;++i) {
u=in(), v=in(), l=in(), h=in();
a[i]=(info){u, v, h};
add_edge(u, v, l);
}
dijkstra();
kruskal(a);
kt::dep[tot]=1;
kt::dfs(tot);
int q=in(), k=in(), s=in(), ans=0, v, a;
while(q--) {
int v=(in()+(ll)k*ans-1)%n+1, a=(in()+(ll)k*ans)%(s+1);
ans=kt::query(v, a);
printf("%d\n", ans);
}
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号