FFT学习笔记
快速傅里叶变换FFT(Fast Fourior Transform)
先说一下它能干嘛qwq
傅里叶变换有两种,连续傅里叶变换和离散傅里叶变换,OI中主要用来快速计算多项式卷积。
等一下,卷积是啥》》
卷积可以通俗地理解成把两个多项式相乘,比如 : \((x^2+x)*(x+2)=x^3+2x^2+2x\)
对于多项式的系数来说,就是求这个柿子:
给定两个多项式 \(A(x), B(x):\)
相乘得到 \(C(x):\)
直接暴力计算复杂度是 \(O(n^2),\) 显然不够优秀\(,\) 所以要用FFT快速计算\(;\)
前置知识
复数初步\(;\) 多项式表达 \(\ldots \ldots\)
正文部分
一、多项式的表达
系数表达\(:\) 一般我们写的形如 \(x^2+5x-1\) 这样的柿子可以表示为向量 \(\vec {a}=(1,5,-1)\)
点值表达\(:\) 给定\(n\)个点\(,\) 可以确定一个\(n-1\)次多项式\(;\) 一个多项式有无数种点值表达\(;\)
将点值表达转换为系数表达的过程叫做插值\(,\) 常用的有拉格朗日插值法 \(;\)
显然对于两个多项式的点值表达横坐标采样点相同\(,\) 就可以直接相乘,时间复杂度\(O(n)\)。
二、复数\((complex)\)初步 \(:\) 单位根
\(n\) 次单位根指满足 \(z^n=1\) 的复数,一共有 \(n\) 个\(,\) 即 \(\omega_n^k=e^{\frac{2 \pi ik}{n}}\) \(,\) $k \in [0 , n-1]; $ (强烈吐槽数学公式渲染qaq
根据欧拉公式 \(e^{i\theta}=\cos(\theta)+i\sin(\theta)\) \(,\) 所以 \(\omega_n^k=cos(\frac{2k \pi}{n})+i\sin(\frac{2k \pi}{n});\)
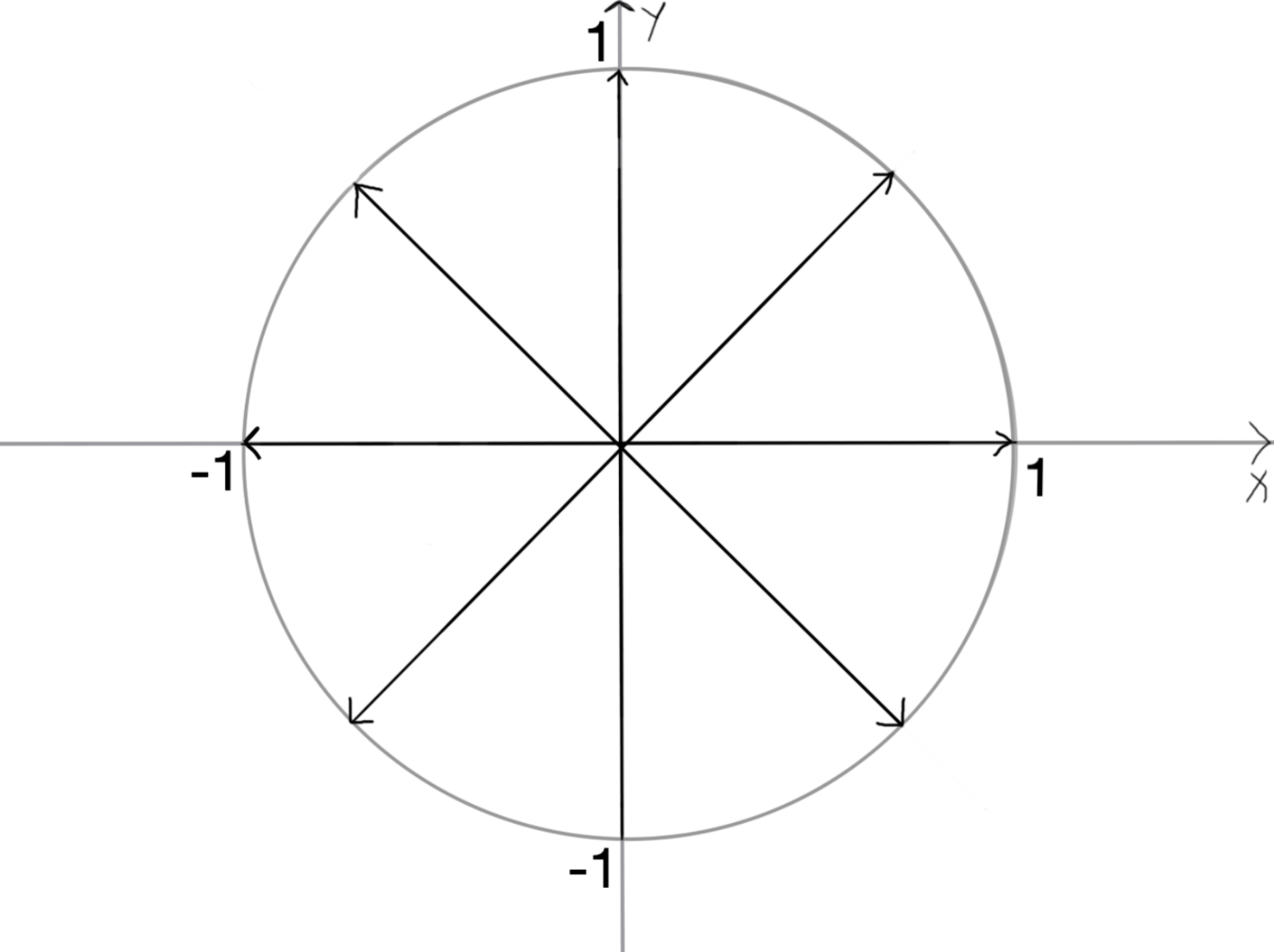
几何意义\(:\) \(n\) 次单位根均匀分布在复平面的单位圆上\(;\) \(p.s.\) 复数相乘\(:\) 模长相乘\(,\) 幅角相加
\(n=8\) 时\(,\) 如下图\(:\)
三、DFT与IDFT
\(1.DFT\)
DFT$(Discrete $ \(Fourier\) \(Transform)\) 可以在 \(O(n\) \(lb\) \(n)\) 的时间内把多项式的系数表达转为点值表达\(;\)
一个多项式的系数表达 \(\vec a=(a_0,a_1,a_2……a_n-1)\) 可以写成一个矩阵列向量\(a:\)
把\(n\)个单位复数根带入该多项式可以得到如下方程组\(;\)
其中\(,\) \(A\)即为点值表达;
写成矩阵形式\(:\)
\(2.IDFT\)
为了方便表示\(,\) 不妨设:
再回顾一下IDFT要解决的问题\(,\) 已知点值表达\(,\) 求系数表达\(,\) 即\(:\) 已知 \(A\) 求 \(a\)
根据DFT的过程\(,\) 显然可以得到\(:\) \(V \cdot a=A\)
问题就转化为 \(a=V^{-1} \cdot A\)
接下来开始填鸭\(:\)
(1) 已知一个复数 \(z=a+bi\) \(,\) 则它的共轭复数为 \(z'=a-bi\) \(,\) 显然 $ z \cdot z' = a^2 + b^2,$
且 \(\omega_n^k\) 的共轭复数为 \(\omega_n^{-k}\) (可以考虑单位根的几何意义)\(;\)
不难发现 \(D\) 中的每个数都是 \(V\) 中对应位置上的共轭复数\(;\)
\(D\) 即为 \(V\) 的共轭矩阵;
(2) 两个共轭复数相乘是一个实数,可以尝试性地写出 \(E=V \cdot D ;\)
当 \(i=j\) 时\(,\) \(e_{i,j}=\sum_{k=0}^{n-1}v_{i,k} \cdot d_{k,j}=\sum_{k=0}^{n-1} (\omega_n^{i-j})^k=n\)
当 $ i \ne j $ 时\(,\) \(e_{i,j}=\sum_{k=0}^{n-1}v_{i,k} \cdot d_{k,j}=\sum_{k=0}^{n-1}(\omega_n^{(i-j)})^k,\) 不难发现这是个等比数列\(,\) 所以\(:\)
\(e_{i,j}=\frac{\omega_n^{(i-j)n}-1} {\omega_n ^ {i-j} - 1}=0\)
综上\(,\) \(E\)是一个$n \times n $ 的矩阵\(:\)
线性代数中\(,\) 矩阵主对角线上的数都是 \(n\) 的矩阵可以看成是数 \(n,\) 这个可以通过矩阵乘法验证\(,\) 不再赘述\(;\)
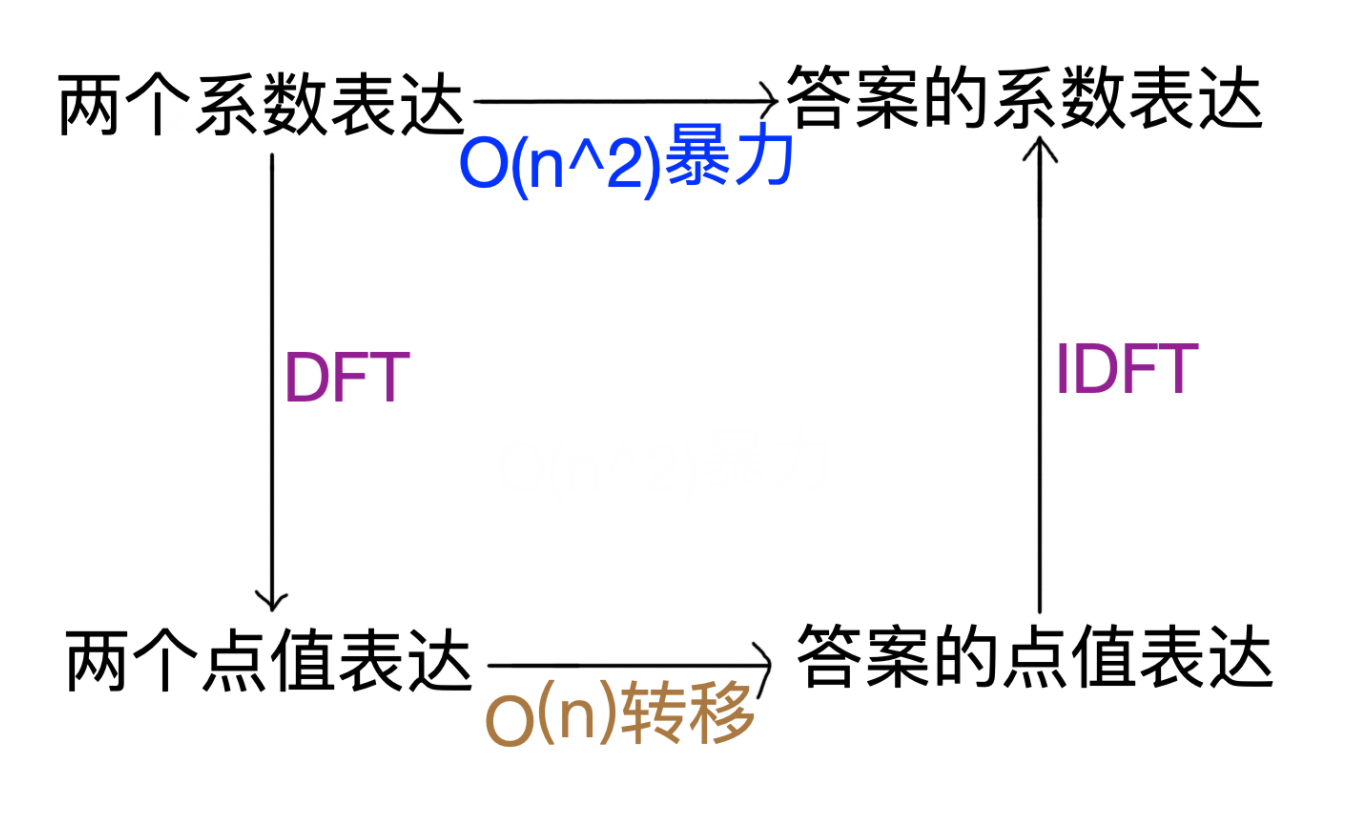
至此\(,\) 求多项式卷积的复杂度仍然是 \(O(n^2),\) 后面的内容就是加速的方法,这里附一张图方便理解\(:\)
四、FFT的实现
\(p.s.\) 这里默认 \(n=2^k, k \in Z\)
关于单位根的一些性质\(:\)
1.消去引理 \(\omega_{dn}^{dk}=e^{\frac{2 \pi idk}{dn}}=e^{\frac{2 \pi ik}{n}}=\omega_n^k\)
2.折半引理 \(\omega_n^{k+ \frac{n}{2}}=-\omega_n^k\)
\(prf:\) \(\because \omega_n^n=1\)
\(\therefore \omega_n^{\frac{n}{2}} = \pm 1\)
又 \(\because \omega_n^{\frac{n}{2}} \ne \omega_n^n\)
\(\therefore \omega_n^{\frac{n}{2}}=-1\)
\(\therefore \omega_n^{k+ \frac{n}{2}}=-\omega_n^k\)
设 \(A_0(x)=a_0x^0+a_2x+a_4x^2+ \cdots +a_{n-2}x^{\frac{n}2-1},\) \(A_1(x)=a_1x^0+a_3x^1+a_5x^2+ \cdots +a_{n-1}x^{\frac{n}2-1}\)
则 \(A(x)=A_0(x^2)+xA_1(x^2);\)
把 \(x=\omega_n^k\) 代入\(,\) 根据消去引理可得\(:\) \((\omega_n^k)^2 = \omega_{\frac{n}{2}}^k\)
所以柿子可以写成\(:\)
直接递归实现就好了\(,\) 和之前说的一样\(,\) 要把 \(n\) 补齐 \(2\) 的次幂\(,\) 代码如下\(;\)
\(p.s.\) 有个小的常数优化 \(——\) 复数手写\(,\) 不用 \(stl\)
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
typedef double db;
typedef long long ll;
inline int in() {
int x=0;char c=getchar();
while(c<'0'||c>'9') c=getchar();
while(c>='0'&&c<='9') x=(x<<1)+(x<<3)+(c^48), c=getchar();
return x;
}
template<typename T>
inline void out(T x) {
int cnt=0;
static char s[20];
do s[cnt++]=x%10; while(x/=10);
while(cnt--) putchar(s[cnt]+48);
putchar(' ');
}
const int N = (int)3e6+5;
const db PI=acos(-1);
struct cp {
db real, imag;
cp(db x=0, db y=0) { this->real=x, this->imag=y; }
inline cp operator + (const cp x) { return cp(this->real+x.real, this->imag+x.imag); }
inline cp operator - (const cp x) { return cp(this->real-x.real, this->imag-x.imag); }
inline cp operator * (const cp x) {
return cp(this->real*x.real-this->imag*x.imag, this->real*x.imag+this->imag*x.real);
}
};
cp x[N], y[N];
int n, m, nn;
void fft(int n, cp *a, int k) {
if(n==1) return ;
int nn=n>>1;
cp a0[nn+1], a1[nn+1];
for(int i=0;i<nn;i++) a0[i]=a[i<<1], a1[i]=a[i<<1|1];
fft(nn, a0, k); fft(nn, a1, k);
cp omega_n(cos(2*PI/n), sin(k*2*PI/n)), omega(1, 0);
for(int i=0;i<nn;i++) {
a[i]=a0[i]+omega*a1[i];
a[i+nn]=a0[i]-omega*a1[i];
omega=omega*omega_n;
}
}
int main() {
n=in(), m=in();
for(int i=0;i<=n;i++) x[i].real=in();
for(int i=0;i<=m;i++) y[i].real=in();
m+=n, nn=1;
while(nn<=m) nn<<=1;
fft(nn, x, 1); fft(nn, y, 1);
for(int i=0;i<nn;i++) x[i]=x[i]*y[i];
fft(nn, x, -1);
for(int i=0;i<=m;i++) out((int)(x[i].real/nn+0.5));
putchar('\n');
return 0;
}
五、迭代实现
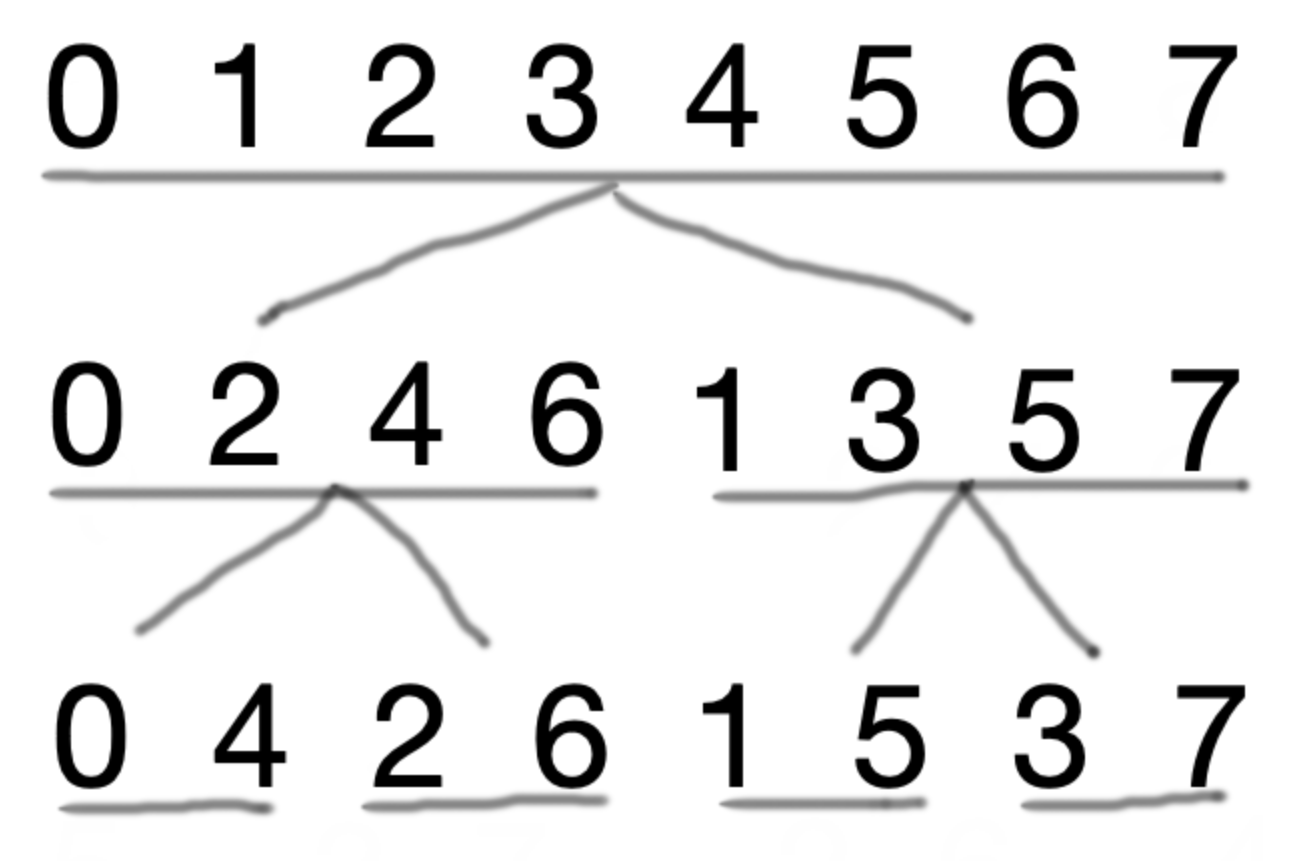
在递归实现时\(,\) 把当前的 \(A\) 奇偶分组\(,\) 实际上是按末尾二进制位分组\(,\) 不妨考虑 \([0, n-1]\) 的二进制\(;\)
每次递归分组时\(,\) 显然二进制是从最低位到最高位产生影响\(,\) 可以得到如下结论\(:\)
\(A\) 中的每个数在递归终止时所在的位置的编号\(,\) 就是把它开始所在位置二进制反过来得到的\(;\)
简单验证一下:
| Before | - | - | End |
|---|---|---|---|
| 0 | 000 | 000 | 0 |
| 1 | 001 | 100 | 4 |
| 2 | 010 | 010 | 2 |
| 3 | 011 | 110 | 6 |
| 4 | 100 | 001 | 1 |
| 5 | 101 | 101 | 5 |
| 6 | 110 | 011 | 3 |
| 7 | 111 | 111 | 7 |
那么问题来了\(,\) 代码怎么实现》》》
\(rev_i=rev_{i/2}/2+(i\) \(mod\) \(2)*(\frac{n}{2})\)
把 \(i\) 右移一位\(,\) 反过来\(,\) 再把之前在开头的 \(0\) 移走\(,\) 再把最后一位的贡献计算出来即可\(;\)
上代码 \(:\)
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
typedef double db;
typedef long long ll;
inline int in() {
int x=0;char c=getchar();
while(c<'0'||c>'9') c=getchar();
while(c>='0'&&c<='9') x=(x<<1)+(x<<3)+(c^48), c=getchar();
return x;
}
template<typename T>
inline void out(T x) {
int cnt=0;
static char s[20];
do s[cnt++]=x%10; while(x/=10);
while(cnt--) putchar(s[cnt]+48);
putchar(' ');
}
const int N = (int)3e6+5;
const db PI=acos(-1);
struct cp {
db real, imag;
cp(db x=0, db y=0) { this->real=x, this->imag=y; }
inline cp operator + (const cp x) { return cp(this->real+x.real, this->imag+x.imag); }
inline cp operator - (const cp x) { return cp(this->real-x.real, this->imag-x.imag); }
inline cp operator * (const cp x) {
return cp(this->real*x.real-this->imag*x.imag, this->real*x.imag+this->imag*x.real);
}
};
cp x[N], y[N];
int n, m, nn, rev[N];
inline void fft(const int n, cp *a, const int k) {
for(int i=1;i<=n;i++) if(i<rev[i]) std::swap(a[i], a[rev[i]]);
for(int len=2;len<=n;len<<=1) {
cp omega_n(cos(2*PI/len), sin(2*PI*k/len));
int m=len>>1;
for(int i=0;i<n;i+=len) {
cp omega(1, 0);
for(int j=i;j<i+m;j++) {
cp t1=a[j], t2=omega*a[j+m];
a[j]=t1+t2, a[j+m]=t1-t2;
omega=omega*omega_n;
}
}
}
if(k==-1)
for(int i=0;i<n;i++) a[i].real=(int)(a[i].real/n+0.5);
}
int main() {
n=in(), m=in();
for(int i=0;i<=n;i++) x[i].real=in();
for(int i=0;i<=m;i++) y[i].real=in();
m+=n, nn=1;
while(nn<=m) nn<<=1;
for(int i=1;i<nn;i++) rev[i]=(rev[i>>1]>>1)|(i&1)*(nn>>1);
fft(nn, x, 1); fft(nn, y, 1);
for(int i=0;i<nn;i++) x[i]=x[i]*y[i];
fft(nn, x, -1);
for(int i=0;i<=m;i++) out((int)(x[i].real));
putchar('\n');
return 0;
}

