0.PTA得分截图

1.本周学习总结(0-5分)
1.1 总结树及串内容
BF算法
bf的原理:从目标串T的的第一个字符起与模式串P的第一个字符比较。
若相等,则继续对字符进行后续的比较;否则目标串从第二个字符起与模式串的第一个字符重新比较。
直至模式串中的每个字符依次和目标串中的一个连续的字符序列相等为止,此时称为匹配成功,否则匹配失败。
举个例子,如果给定文本串S“BBC ABCDAB ABCDABCDABDE”,和模式串P“ABCDABD”,现在要拿模式串P去跟文本串S匹配,整个过程如下所示:
1、S[0]为B,P[0]为A,不匹配,执行第②条指令:“如果失配(即S[i]! = P[j]),令i = i - (j - 1),j = 0”,S[1]跟P[0]匹配,相当于模式串要往右移动一位(i=1,j=0)

- S[1]跟P[0]还是不匹配,继续执行第②条指令:“如果失配(即S[i]! = P[j]),令i = i - (j - 1),j = 0”,S[2]跟P[0]匹配(i=2,j=0),从而模式串不断的向右移动一位(不断的执行“令i = i - (j - 1),j = 0”,i从2变到4,j一直为0)

- 直到S[4]跟P[0]匹配成功(i=4,j=0),此时按照上面的暴力匹配算法的思路,转而执行第①条指令:“如果当前字符匹配成功(即S[i] == P[j]),则i++,j++”,可得S[i]为S[5],P[j]为P[1],即接下来S[5]跟P[1]匹配(i=5,j=1)

- S[5]跟P[1]匹配成功,继续执行第①条指令:“如果当前字符匹配成功(即S[i] == P[j]),则i++,j++”,得到S[6]跟P[2]匹配(i=6,j=2),如此进行下去

- 直到S[10]为空格字符,P[6]为字符D(i=10,j=6),因为不匹配,重新执行第②条指令:“如果失配(即S[i]! = P[j]),令i = i - (j - 1),j = 0”,相当于S[5]跟P[0]匹配(i=5,j=0)

- 至此,我们可以看到,如果按照暴力匹配算法的思路,尽管之前文本串和模式串已经分别匹配到了S[9]、P[5],但因为S[10]跟P[6]不匹配,所以文本串回溯到S[5],模式串回溯到P[0],从而让S[5]跟P[0]匹配。

KMP算法
kmp算法的原理:通过子串的对称性,将匹配效率提高的方法
next[i]就是计算子串的对称性,下面通过1个例子来看如何构造。
例子1:cacca有5个前缀,求出其对应的next数组。
前缀2为ca,显然首尾没有相同的字符,next[2] = 0
前缀3为cac,显然首尾有共同的字符c,故next[3] = 1
前缀4为cacc,首尾有共同的字符c,故next[4] = 1
前缀5为cacca,首尾有共同的字符ca,故next[5] = 2
kmp算法流程:
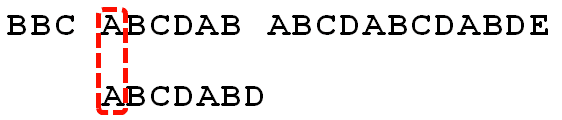
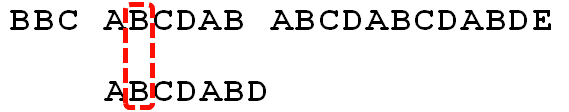

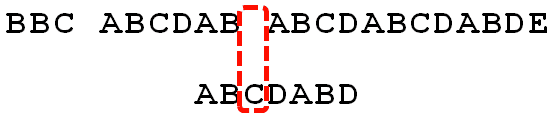
假设现在文本串S匹配到i位置,模式串P匹配到j位置
当前字符匹配成功(即S[i] == P[j],图一),都令k++,j++,继续匹配下一个字符;
当前字符匹配失败(即S[i] != P[j],图二),则令 k不变,j = next[j]。此举意味着失配时,模式串P相对于文本串S向右移动了j - next [j]位。
换言之,当匹配失败时,模式串向右移动的位数为:失配字符所在位置 - 失配字符对应的next 值
二叉树结构
顺序结构
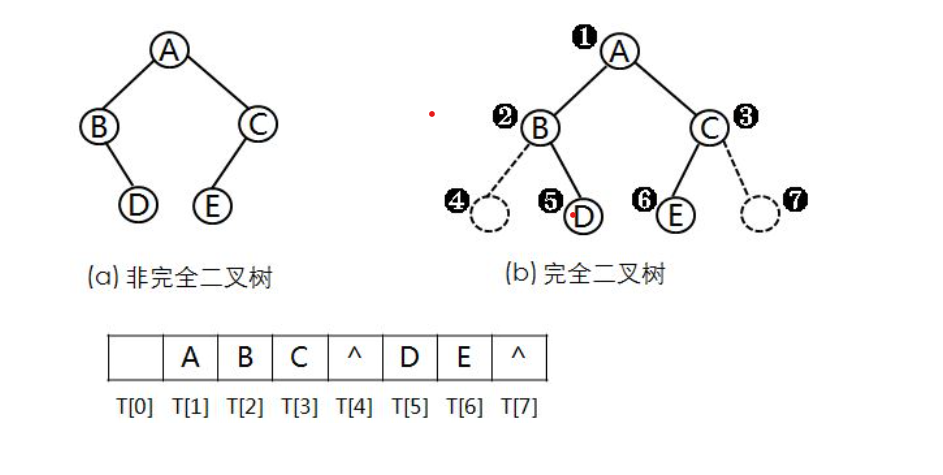
二叉树的顺序存储:用一组连续的存储单元存放二叉树中的结点。即用一维数组存储二叉树中的结点。因此,必须把二叉树的所有结点安排成一个恰当的序列,结点在这个序列中的相互位置能反映出结点之间的逻辑关系。用编号的方法从树根起,自上层至下层,每层自左至右地给所有结点编号。
在非完全二叉树中添加一些并不存在的空结点使之变成完全二叉树,(把不存在的结点设置为“^”)不过这样做有可能会造成空间的浪费,如下图所示,然后再用一维数组顺序存储二叉树。
链式存储结构
二叉树的每个结点最多有两个孩子,因此,每个结点除了存储自身的数据外,还应设置两个指针分别指向左、右孩子结点。
结点结构如下图所示:

操作
前序遍历:
void PreOrder(BTreeNode* BT) {
if(BT != NULL) {
cout << BT->data << ' ';
PreOrder(BT->left);
PreOrder(BT->right);
}
}
中序遍历:
void InOrder(BTreeNode* BT) {
if(BT != NULL) {
InOrder(BT->left);
cout << BT->data << ' ';
InOrder(BT->right);
}
}
后序遍历:
void PostOrder(BTreeNode* BT) {
if(BT != NULL) {
PostOrder(BT->left);
PostOrder(BT->right);
cout << BT->data << ' ';
}
}
层次遍历:
void AllPath2(BTree b)
{
int k;
BTree p;
QuType *qu;
InitQueue(qu);
b->parent=-1;
enQueue(qu,b);
while (!QueueEmpty(qu))
{
deQueue(qu,p);
if (p->lchild==NULL && p->rchild==NULL)
{
k=qu->front;
while (qu->data[k]->parent!=-1)
{
printf("%c->",qu->data[k]->data);
k=qu->data[k]->parent;
}
printf("%c\n",qu->data[k]->data);
}
}
}
先序建树:
BTree CreatTree(string str, int &i)
{
BTree bt;
if (i > len - 1) return NULL;
if (str[i] == '#') return NULL;
bt = new BTNode;
bt->data = str[i];
bt->lchild = CreatTree(str, ++i);
bt->rchild = CreatTree(str, ++i);
return bt;
}
中序建树:
BTree CreatTree(string str, int &i)
{
BTree bt;
if (i > len - 1) return NULL;
if (str[i] == '#') return NULL;
bt = new BTNode;
bt->lchild = CreatTree(str, ++i);
bt->data = str[i];
bt->rchild = CreatTree(str, ++i);
return bt;
}
后序建树:
BTree CreatTree(string str, int &i)
{
BTree bt;
if (i > len - 1) return NULL;
if (str[i] == '#') return NULL;
bt = new BTNode;
bt->lchild = CreatTree(str, ++i);
bt->rchild = CreatTree(str, ++i);
bt->data = str[i];
return bt;
}
线索二叉树
二叉树的结点上加上线索的二叉树称为线索二叉树,对二叉树以某种遍历方式(如先序、中序、后序或层次等)进行遍历,使其变为线索二叉树的过程称为对二叉树进行线索化。
线索二叉树中的线索能记录每个结点前驱和后继信息。为了区别线索指针和孩子指针,在每个结点中设置两个标志ltag和rtag。
当tag和rtag为0时,leftChild和rightChild分别是指向左孩子和右孩子的指针;否则,leftChild是指向结点前驱的线索(pre),rightChild是指向结点的后继线索(suc)。由于标志只占用一个二进位,每个结点所需要的存储空间节省很多。

其中:ltag=0 时lchild指向左儿子;ltag=1 时lchild指向前驱;rtag=0 时rchild指向右儿子;rtag=1 时rchild指向后继。
哈夫曼树
哈夫曼树,又称最优树,是一类带权路径长度最短的树。首先有几个概念需要清楚:
1、路径和路径长度
从树中一个结点到另一个结点之间的分支构成两个结点的路径,路径上的分支数目叫做路径长度。树的路径长度是从树根到每一个结点的路径长度之和。
2、带权路径长度
结点的带权路径长度为从该结点到树根之间的路径长度与结点上权的乘积。树的带权路径长度为树中所有叶子结点的带权路径长度之和,通常记作WPL。
若有n个权值为w1,w2,...,wn的结点构成一棵有n个叶子结点的二叉树,则树的带权路径最小的二叉树叫做哈夫曼树或最优二叉树。

在上图中,3棵二叉树都有4个叶子结点a、b、c、d,分别带权7、5、2、4,则它们的带权路径长度为
(a)WPL = 72 + 52 + 22 + 42 = 36
(b)WPL = 42 + 73 + 53 + 21 = 46
(c)WPL = 71 + 52 + 23 + 43 = 35
其中(c)的WPL最小,可以验证,(c)恰为哈夫曼树。
并查集
把每个数据所在集合初始化为其自身。
查找元素所在的集合,即根节点。
根节点父亲为本身
将两个元素所在的集合合并为一个集合。
合并之前,应先判断两个元素所在树的高度。
1.2 对树的认识及学习体会
太难了,我觉得我很多都不会!!!!!!!!!!!!!
2.阅读代码
2.1题目及解题代码

class Solution {
public:
bool isSymmetric(TreeNode* root) {
if(!root) return true;
return __isSymmetric(root->left, root->right);
}
bool __isSymmetric(TreeNode* root1, TreeNode* root2){
bool flag1, flag2;
if(root1==nullptr){
if(root2!=nullptr) return false;
return true;
}
else if(root1!=nullptr){
if(root2==nullptr) return false;
//
if(root1->val!=root2->val) return false;
flag1 = __isSymmetric(root1->left, root2->right);
flag2 = __isSymmetric(root1->right, root2->left);
}
return flag1&&flag2;
}
};
2.1.1 该题的设计思路
通过递归判断对称性
2.1.2 该题的伪代码
if两个子树都为空
return false;
else return true;
else if(root1不为空)
if(root2) return false;
if两个子树都不为空
return false;
递归
2.1.3 运行结果
2.1.4分析该题目解题优势及难点
题目思路清晰,对递归要求较高




