0.PTA得分截图

1.本周学习总结(0-4分)
1.1 总结栈和队列内容
栈的存储结构及操作
一、栈
其实本质还是线性表:限定仅在表尾进行插入或删除操作。 俗称:后进先出 (LIFO=last in first out结构),也可说是先进后出(FILO)。
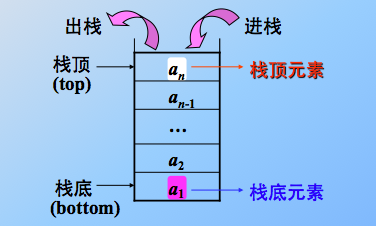
顺序栈:利用一组地址连续的存储单元依次存放自栈底到栈顶的数据元素,同时附设指针 top 指示栈顶元素在顺序栈中的位置,附设指针 base 指示栈底的位置。 同样,应该采用可以动态增长存储容量的结构。且注意,如果栈已经空了,再继续出栈操作,则发生元素下溢,如果栈满了,再继续入栈操作,则发生元素上溢。栈底指针 base 初始为空,说明栈不存在,栈顶指针 top 初始指向 base,则说明栈空,元素入栈,则 top++,元素出栈,则 top--,故,栈顶指针指示的位置其实是栈顶元素的下一位(不是栈顶元素的位置)。
1empty()函数
2size()函数
3push()压栈函数
4pop()出栈函数
5top()输出栈顶元素函数
6
7
8
9 typedef struct{
10 int stackSize;//栈容量
11 char *base;//栈底指针
12 char *top;//栈顶指针
13 } SqStack;
14
15 //初始化
16 //本质还是使用动态数组
17 void initStack(SqStack *s)
18 {
19 s->base = (char *)malloc(STACK_SIZE * sizeof(char));
20 //分配成功
21 if (s->base != NULL) {
22 //空栈
23 s->top = s->base;
24 s->stackSize = STACK_SIZE;
25 }
26 else
27 {
28 puts("分配失败!");
29 }
30 }
31
32 //判空
33 bool isEmpty(SqStack s)
34 {
35 return s.top == s.base ? true : false;
36 }
37
38 //判满
39 bool isFull(SqStack s)
40 {
41 return (s.top - s.base) >= STACK_SIZE ? true : false;
42 }
43
44 //求当前长度
45 int getLength(SqStack s)
46 {
47 int i = 0;
48 char *q = s.top;
49
50 while (q != s.base) {
51 q--;
52 i++;
53 }
54
55 return i;
56 }
57
58 //求栈顶元素
59 char getTop(SqStack s, char topElement)
60 {
61 if (isEmpty(s)) {
62 puts("栈空!");
63 }
64
65 topElement = *(s.top - 1);
66 return topElement;
67 }
68
69 //入栈
70 void push(SqStack *s, char topElement)
71 {
72 char *q = NULL;
73
74 if (isFull(*s)) {
75 q = (char *)realloc(s->base, STACK_INCREMENT * sizeof(char));
76
77 if (NULL == q) {
78 exit(0);
79 }
80
81 s->base = q;
82 s->stackSize = s->stackSize + STACK_INCREMENT;
83 }
84 //进栈
85 *s->top++ = topElement;
86 }
87
88 //出栈
89 void pop(SqStack *s, char *topElement)
90 {
91 if (isEmpty(*s)) {
92 exit(0);
93 }
94
95 s->top--;
96 *topElement = *s->top;
97 }
98
99 //遍历
100 void traversal(SqStack s)
101 {
102 for (int i = 0; i < getLength(s); i++) {
103 printf("栈中元素遍历:%c \n", s.base[i]);
104 }
105 }
106
107 //清空
108 void cleanStack(SqStack *s)
109 {
110 if (!isEmpty(*s)) {
111 s->top = s->base;
112 puts("栈已经清空!");
113 }
114 }
115
116 //销毁
117 void destroyStack(SqStack *s)
118 {
119 if (s->base != NULL) {
120 free(s->base);
121 s->base = NULL;
122 s->top = NULL;
123 s->stackSize = 0;
124 puts("栈成功销毁!");
125 }
126 }
栈的应用
- 进制转换
在计算机中存储的数据都是二进制,所以往往需要把十进制数据转换成二进制,转换的过程实际就是除2取余数,这其中我们可以看到最先求得余数实际是个位数,书写一个数据的时候都是先书写高位的数据,而后依次到个位。这正好和栈后进先出的特性吻合,因此可以使用栈来存储。
例如:十进制的25转换成2进制
25 25/2 25%2 n 0==n/2 y=n%2
25 12 1
12 6 0
6 3 0
3 1 1
1 0 1
根据最后得到的是高位,先除余得到的是个位,最后得到的二进制值是:11001 - 括号匹配
判断一个表达式的”(“和”)”是否匹配,思路是这样的:遇到”(“则入栈,遇到”)”则从栈顶弹出”(“与之配成一对,当整个表达式扫描完毕时:
(1) 若栈内为空,则说明(与)是匹配的。
(2) 若表达式扫描完毕,栈内仍有(则说明左括号是多的。
(3) 若当)被扫描到,栈里却没有(能弹出了,说明)多,表达式中)也是多的。 - 表达式求值
算法思想:
(1) 首先置操作数栈OPND为空栈,表达式的起始符#为运算符栈OPTR的栈底元素;
(2) 依次读入表达式中的每个字符
若运算符是‘#’或栈顶是‘#’,结束计算,返回OPND栈顶值。
if(是操作数) → 则PUSH( OPND,操作数);
if(是运算符) → 则与OPTR栈顶元素进行比较,按优先级进行操作;
优先级操作细则如下:
① if栈顶元素<输入算符,则算符压入OPTR栈,并接收下一字符
② if栈顶元素=运算符但≠‘#’,则脱括号(弹出左括号)并收下一字;
③ if栈顶元素>运算符,则退栈、按栈顶计算,将结果压入OPND栈。
④ 且该未入栈的运算符要保留,继续与下一个栈顶元素比较!
表达式求值过程的描述:3*(7 – 2 )
队列的存储结构及操作
队列是一种特殊的线性表,特殊之处在于它只允许在表的前端(front)进行删除操作,而在表的后端(rear)进行插入操作,和栈一样,队列是一种操作受限制的线性表。进行插入操作的端称为队尾,进行删除操作的端称为队头。队列中没有元素时,称为空队列。
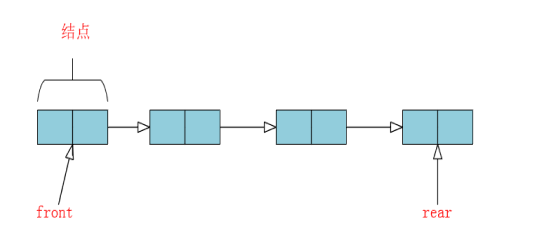
链式队列的构建:
//链式队列 链式结构+队列
//链式结构体 =单链表的基本单元:结点
struct Node{
int data;//数据域
struct Node* next; //指针域
};
//队列结构体=头指针+尾指针+队列大小
struct Queue{
struct Node* front;//指向结点的头指针
struct Node* rear;//指向结点的尾指针
int queueSize; //队列大小/长度
};
创建结点:
//创建结点
struct Node* createNode(int data){
struct Node* newNode=(struct Node*)malloc(sizeof(struct Node));
newNode->next=NULL;
newNode->data=data;
return newNode;
};
队列的初始化:
//队列初始化
struct Queue* createQueue(){
struct Queue* queue=(struct Queue*)malloc(sizeof(struct Queue));//分配内存空间
queue->front=queue->rear=NULL;//头指针和尾指针在一起为空
queue->queueSize=0;//队列大小为0
return queue;
}
入队操作:
void push(struct Queue* queue,int data){
struct Node* newNode=createNode(data);
if(queue->queueSize==0)
queue->front=newNode;
else
queue->rear->next=newNode;
queue->rear=newNode;
queue->queueSize++;
}
获取对头元素:
//获取对头元素
int queryFront(struct Queue* queue) {
if(queue->queueSize==0){
printf("队列为空无法获取对头元素");
printf("\n");
return -1;
}
return queue->front->data;
}
判断队列是否为空:
//判断队列是否为空
int empty(struct Queue* queue){
if(queue->queueSize==0)
return 0;
else
return 1;
}
出队操作:
//出队操作
void pop (struct Queue* queue){
if(queue->queueSize==0){
printf("队列为空不能出队");
exit(0);
}else{
struct Node* newFrontNode=queue->front->next;
free(queue->front);
queue->front=newFrontNode;
queue->queueSize--;
}
}
队列应用
在具体的程序设计中,只要涉及到先进先出的设计,即采用了队列的思想。
队列的一个典型应用就是求解——迷宫问题。
迷宫问题是指:给定给定一个M×N的迷宫图、入口与出口、行走规则。求一条从指定入口到出口的路径。
所求路径必须是简单路径,即路径不重复。
迷宫问题可以用栈或者队列来求解。其中使用队列求解出的路径是最短路径。
迷宫采用二维数组来表示,其中路用0表示,墙用1表示。为了求解问题的方便,通常在数组的周围加上围墙,即在周围加上两行和两列。形成M+2行,N+2列的迷宫数组。
求解思路:使用顺序队列(使用顺序队列的原因是:出队入队操作并不会删除结点,只是改变了队首队尾指针的值,最终还要通过队列中已出队节点来回溯得到路径),队列中的数据元素类型为格点坐标(i,j)和路径中上一格点在队列中的位置pre的封装。pre的设置是为了找到终点后由终点通过pre回溯到起点从而逆序打印出路径(采用递归实现)。在将一个能走的格点入队后,循环搜索它周围的四个格点,并将其中能走的入队,所以必须制定四个方向的搜索顺序(最后若有多条最短路径,则打印出哪一条由搜索顺序决定)。由于路径不重复,所以在在入队后将一个迷宫格点的值赋为-1,避免重复搜索。整体思路类似于广度优先搜索。
1.2.谈谈你对栈和队列的认识及学习体会。
通过课本上对于栈和队列的基本操作函数的学习,不仅学会了如何入栈出栈、入队出队,而且了解了栈空、栈满的条件,并了解了共享栈、链栈、循环队列......等更深入的知识。有过之前对于顺序表的学习,这些都还是比较简单的。当然,无论是栈的后入先出还是队列的先入先出,需要对栈和队列的概念的理解要深刻
2.PTA实验作业(0-2分)
2.1.符号配对
2.1.1代码截图
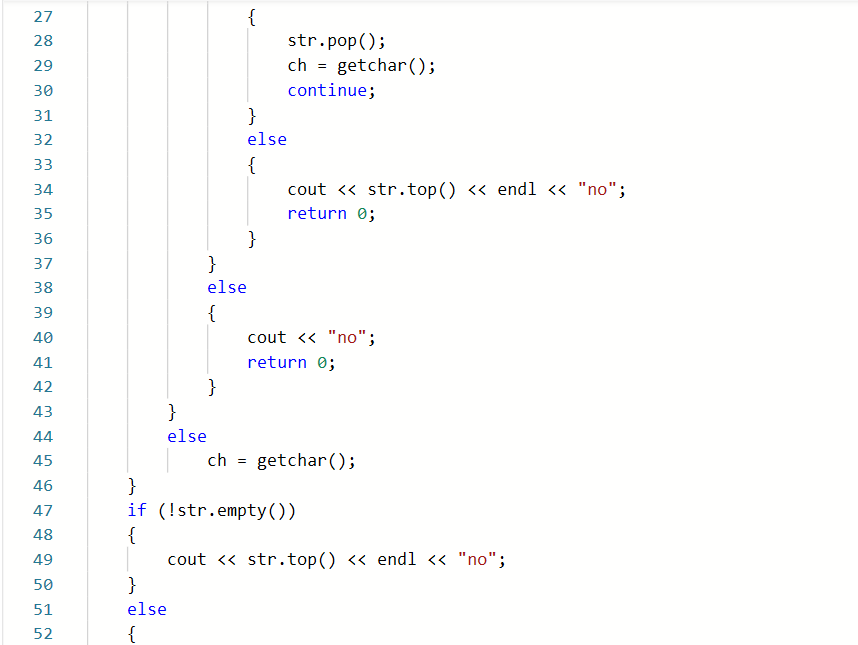
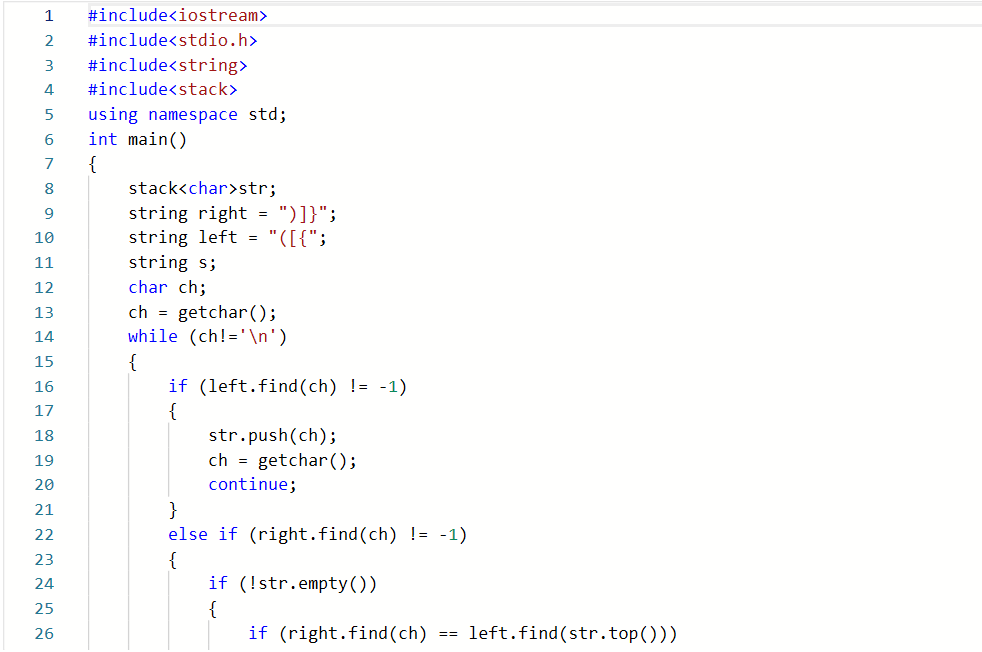
2.1.2本题PTA提交列表说明。

一直部分正确的原因:循环内的条件写错了,导致有时候在特定情况下,跳过一些符号
2.2.银行业务队列简单模拟
2.2.1代码截图
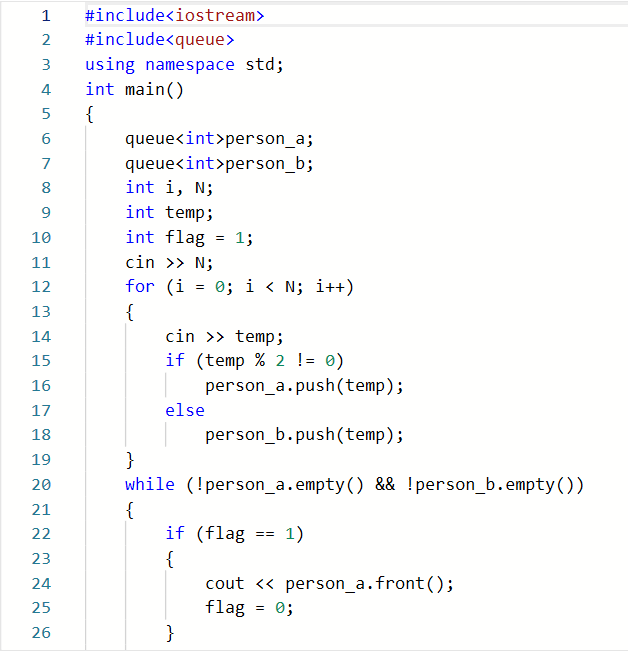
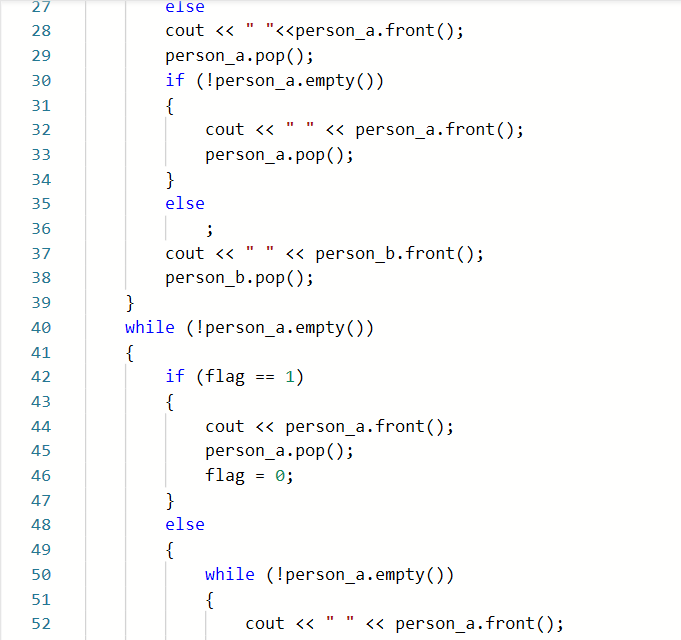

2.2.2本题PTA提交列表说明。

一开始一直有N最少时过不了,后来发现是因为判断输出条件写错了
3.阅读代码(0--4分)
3.1 题目及解题代码
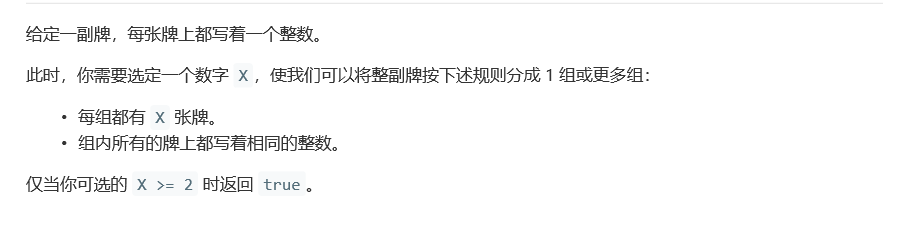

3.1.1 该题的设计思路
任意数与0的gcd是自身,利用这个特性可以直接跳过了所有数量为0的牌,省去cnt[i]非零的判断,同时循环内的if(~g)也可以省去,代码极度简洁,方法非常巧妙。
3.1.2 该题的伪代码
class Solution {
int cnt[10000];
public:
bool hasGroupsSizeX(vector<int>& deck) {
for (auto x: deck) cnt[x]++;
在循环内,通过辗转相除法求出
输出
}
};
3.1.3 运行结果

3.1.4分析该题目解题优势及难点。
优点:题目简短,容易理解,思维清晰
难点:辗转相除法忘了怎么写
3.2 题目及解题代码

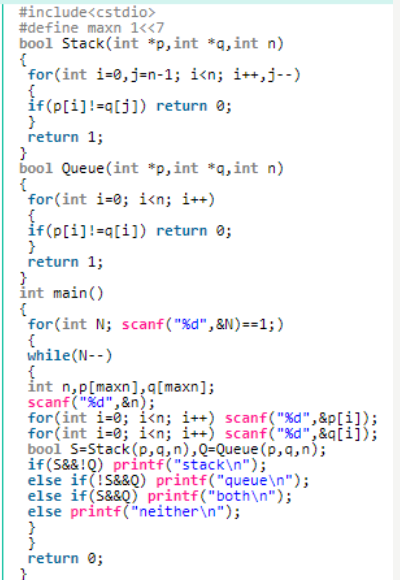
3.2.1 该题的设计思路
建立两个函数,分别用来判断是栈还是队列
如果正着与反着相同,即为栈
如果正着遍历相同,即为队列
3.2.2 该题的伪代码
#include<cstdio>
#define maxn 1<<7
bool Stack(int* p, int* q, int n)//判断栈
{
for (从头开始遍历p数组,从尾开始遍历q数组)
{
if (遍历对比,有一个不相同) return 0;
}
遍历完后return 1;
}
bool Queue(int* p, int* q, int n)//判断队列
{
for (均从头遍历数组q,p)
{
if (遍历对比,有一个不相同) return 0;
}
遍历完后return 1;
}
int main()
{
for (int N; scanf("%d", &N) == 1;)
{
while (N--)
{
定义长度n,两个数组p和q
for (数据读入数组p)
for (数据读入数组q)
bool S = Stack(p, q, n), Q = Queue(p, q, n);//把判断是否是栈和队列的结果存入S和Q中
if (S && !Q) printf("stack\n");
else if (!S && Q) printf("queue\n");
else if (S && Q) printf("both\n");
else printf("neither\n");
}
}
return 0;
}
3.2.3 运行结果

3.2.4分析该题目解题优势及难点。
优点:充分体现了分模块编程的优势。如果不分模块,将面临代码量大、代码重复等问题。
函数分装恰到好处,四种情况封装两个函数,之后通过分支结构进行解决。而不是封装四个函数。
难点 :单单判断是否是栈或队列很容易
难就难在,是栈非队,是队非栈,是栈且队,非栈非队等四种情况的判断上




