0.展示PTA总分


1.本章学习总结
1.1 学习内容总结
循环基本结构
for循环:
for (表达式1; 表达式2; 表达式3)
{
循环体语句;
}
while循环:
while (表达式)
{
循环体语句;
}
do-while循环:
do
{
循环体语句;
} while (表达式);
判断优先使用哪一种循环结构的关键:寻找题目中的条件,判断循环次数是否确定。
若循环次数为常数,则采用for循环,反之选择while循环。
嵌套循环
- 嵌套循环由上述3种基本循环类型所组成的代码块。
- 在阅读嵌套循环或写嵌套循环的过程中,十分需要注意单个循环的结构和位置,防止将各个循环之间的某些变量或条件混肴。
重要语句
- break; :强制循环结束
- continue; :跳过循环体中continue后面的语句,继续下一次循环
- while (1) :恒真循环语句
- while (i) : 循环执行条件是i不等于0,也就是只要i不等于0,就进入while循环
- while (!i) : 循环执行条件是i等于0,也就是只要i等于0,就进入while循环
- pi = ch - '0' :让变量ch转化为数值并赋值给pi
- ch = ch - 'a' + 'A' :小写转化为大写
- ch = ch - 'A' + 'a' :将大写转化为小写
- a++; : a值加1,而整个表达式为执行前的值
- ++a; : a值加1,整个表达式也为执行后的值
1.2 本章学习体会
- 作业量加大,难度变高,需要提前预习才可以跟上老师讲的内容。
- pta里面的题有时候只有30行左右的题目可是自己就是想不出来,逻辑思维和解决问题的能力有待提高
- 本周代码量大概880行
2.PTA实验作业
2.1

2.1.1
数据处理:定义n, i, j, m, t整型变量,引入flag标识符作为判断是否有无素数。
伪代码:
输入n
t←pow(2, n) - 1
for t←2 to t
do m ← pow(2, i) - 1
for j←2 to sqrt (m)
if m求余j等于0 then
do 退出循环
if j > sqrt(m) && m <= t then
do 输出m 且flag←1
if flag等于0 then
do 输出None
2.1.2 代码截图
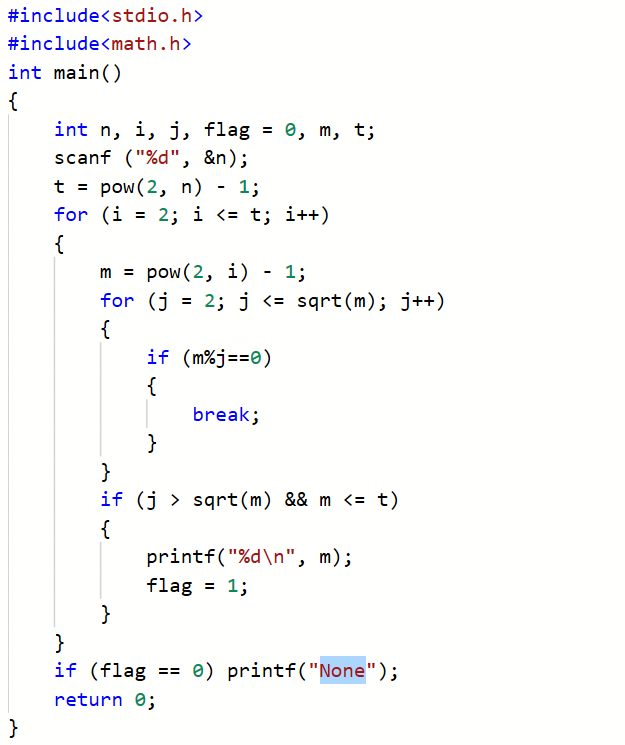
2.1.3 造测试数据
| 输入数据 | 输出据 | 说明 |
|---|---|---|
| 1 | None | 无梅森数 |
| 2 | 3 | 正常数据 |
| 6 | 3 7 31 | 多个数据,格式正确 |
2.1.4 PTA提交列表及说明

- 其实刚开始拿到这道题很懵,因为可能之前上课没有认真听,不知道引入标识符flag来判断是否有素数。在这一点上纠结了很久
- 由于设置变量有点多且个人习惯,所以在编写程序中,我都是把变量放在后面定义,以至于在出现了有一些变量未被定义,称为未标识符
2.2

2.2.1
数据处理:定义c5, c2, c1, cnt , x分别为五分硬币,二分硬币,一分硬币的数量,换法种数,零钱数额。
伪代码:
输入零钱数额
for(五分硬币从19到1)
for(二分硬币从49到1)
for(一分硬币从99到1)
if(当各硬币的数量乘以其面值等于需兑换的总金额时){
输出各种硬币的数量和换法种数
换法种数自加一
}
2.2.2 代码截图
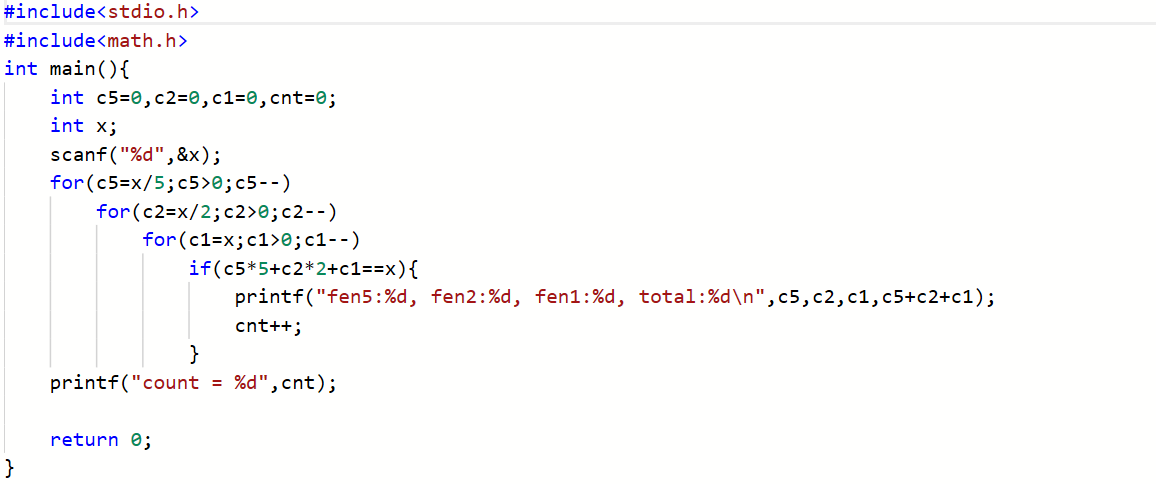
2.2.3 造测试数据
| 输入数据 | 输出数据 | 说明 |
|---|---|---|
| 9 | fen5:1, fen2:1, fen1:2, total:4 count=1 | 一般sample |
| 8 | fen5:1, fen2:1, fen1:1, total:3 count=1 | 最小金额数 |
2.2.4 PTA提交列表及说明

- 虽然这次提供的是2次正确的提交列表,但是我确实想了很久,因为虽然想到了老师上课讲的用嵌套循环再加一个等式来判断,但是我一开始在vs上用的是变量自增,
导致我一直搞不清限制变量的常数,最后想了挺久的,才发现可以用自减,就发现自己好傻
2.3

2.3.1
数据处理:定义一个int p(int a,int b)函数用来计算幂次方之和。
伪代码:
输入n
for (定义i等于m加到v)
{
定义k等于i,sum等于0
while (k大于0)
{
t=k%10;
k=k/10;
sum=sum+p(t,n)
}
if (sum=i)
输出i
2.3.2 代码截图
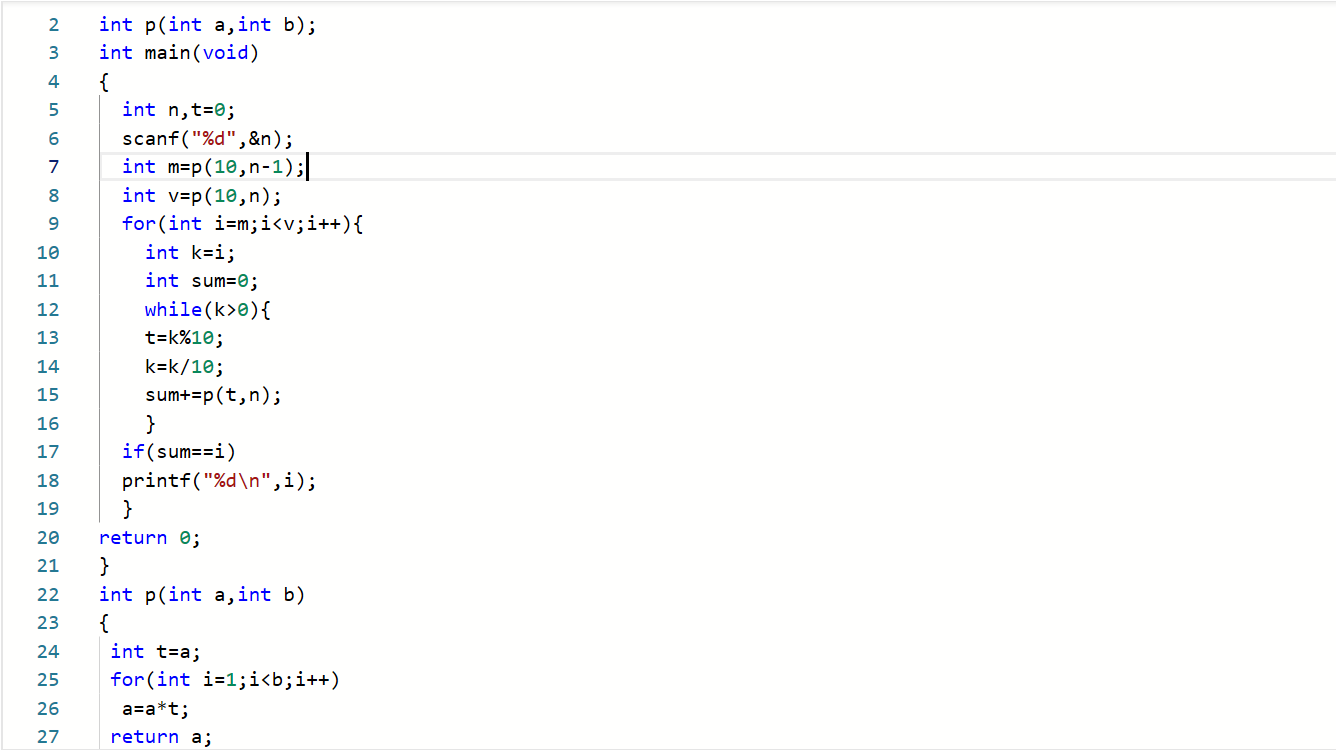
2.3.3 造测试数据
| 输入数据 | 输出数据 | 说明 |
|---|---|---|
| 3 | 153,370,371,407 | 一般sample |
| 6 | 548834 | 一般sample |
2.3.4 PTA提交列表及说明

- 答案错误的原因:忘记设置一个变量k代替i去进行循环里的计算,导致循环过后i的值变了,所以就错了。
3. 代码互评
1.

2.

其实这2段代码的区别主要就是在时间,距离如何计算以及对休息时间的判断。
1.毫无疑问,第二种代码无疑简洁很多,它不仅引入了flag标识符,来判断是否休息,并且在设置变量上也有一定的技巧,使得所设置的变量减少。但是这种方法对我来说,一开始,我很难想到,所以我更记住这种简洁的方法,应用到以后更加复杂的代码中。
2.休息时间的判断:在第一种代码中,采用数学上的求余.而第二种则是采用是否等于0,然后重新等于0来计算。第二种来说,对我是一种较新的方法。
3.当然第二段代码也有不足之处,在于变量名使用不规范,导致我在读这段代码多花了挺长时间的。




