蓝墨云活动三种查找算法练习的分析博客

蓝墨云活动三种查找算法练习的分析博客

活动要求

这次实践是针对三种查找算法的练习
具体要求：给定关键字顺序11,78,10,1,3,2,4,21，试分别用顺序查找、折半查找、散列查找（用探查法和链地址法）来实现查找。试画出他们的对应存储形式（顺序查找的顺序表，二分查找的顺序表，两种散列查找的顺序表），并求出每一种找的成功平均查找长度。其中，散列函数H（k）=k%11。

说明

由于有些操作无法在博客园中显示，所以我在word文件中做了然后截图过来。word文件链接

具体分析

顺序查找的顺序表

由于顺序查找的方法是从第一个开始进行依稀与被查找对象进行比较。所以从头开始查找每个元素所需要的次数依次为。
11:1
78:2
10:3
1:4
3:5
2:6
4:7
21:8
总共进行的查找次数为1+2+3+4+5+6+7+8=36（次）
查找每个元素的概率为：1/8
所以顺序查找的平均查找长度为ASL=36×1/11=9/2

二分查找
二分查找的顺序表

由于二分查找首先要进行排序所以的得到的顺序表应该是一个排好序的列表然后进行查找，按照原理首先应该是先比较列表中间的元素。

这个树状图中的数字表示顺序表中对应的索引每一层的层数则表示查找次数
这是二分查找对应的代码

 public static <T extends Comparable<T>>  
      boolean binarySearch(T[] data, int min, int max, T target)
    {  
        boolean found = false;
        int midpoint = (min + max) / 2;  // 确定中点值

        if (data[midpoint].compareTo(target) == 0)
            found = true;

        else if (data[midpoint].compareTo(target) > 0)
        {
            if (min <= midpoint - 1)
                found = binarySearch(data, min, midpoint - 1, target);
        }
        
        else if (midpoint + 1 <= max)
            found = binarySearch(data, midpoint + 1, max, target);

        return found;
    }
}

由于指针是由最大值和最小值的和，即mid=min+max来决定的，根据代码是无法正常运行的，但是当指针不是整数时可以选择向左偏。
以数字1为例进行讲解
第一个进行比较的元素是第四个元素，也就是数字4。

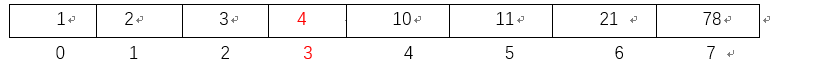
第二步：数字1比4小所以将数字1和4 左边的数字的中间元素进行比较，即与数字2进行比较。

第三步：将1与数字1进行比较。找到数字1。
结合步骤分析与树形图的分析得到。
依此分析，每个元素被找到所需要进行的查找次数为
1:3次
2:2次
3:3次
4:1次
10:3次
11:2次
21:3次
78:4次
总共要进行的查找步数为
1＋2×2＋3×4＋4=21
每个元素被查找的概率为1/8
二分查找的ASL=21×1/11=21/8.

散列查找的两种方法分析
因为散列查找需要借助Hash函数，所以在确定顺序表时也要借助Hash函数
H（k）=k%11；
给定的元素为11,78,10，1,3,2,4，21
11%11=0
78%11=1
10%11=10
1%11=1
2%11=2
3%11=3
4%11=4
21%11=10;
线性搜查
思路，先按照取余得到的值进行插入，然后如果后面的值进行取余与前面的冲突，就将后面的值的余数加一再次进行取余，直到可以插入为之。
用公式来表示大概就是
key，key1表示插入的索引位置
H（k）=k%11=key；
H（k1）=k1%11=key1；
While（num[key1]!=null）
key1=H（key1+1）
按照此原理11应该被插入到0处，78被插到1处，10被插到10处，
因为1%11=1与78冲突，所以应该（1+1）%11=2，将1插入2处，
2%11=2，与1冲突，所以（2+1）%11=3，将2插入3处
3%11=3与2冲突，所以（3+1）%11=4，将3插入4处
4%11=4与3冲突，所以（4+1）%11=5，将4插入5处
21%11=10与10冲突，所以（10+1）%11=0与11冲突，所以（0+1）%11=1与78冲突，所以（1+1）%11=2与1冲突，所以（2+1）%11=3与2冲突，所以（3+1）%11=4与3冲突，所以（4+1）%11=5与5冲突所以将21插入6处。
这样就可以得到

在进行查找时也是按照Hash函数，如果找不到就将余数加一再模11直至找到为止
查找过程展示

被查找元素	查找过程	查找次数
11	11%11=0;int[0]=11查找成功	1
78	78%11=1；int[1]=78查找成功;	1
10	10%11=10；int[10]=10,查找成功;	1
1	1%11=1;（int[1]=78≠11),(1+1）%11=2 ：int[2]=1查找成功；	2
3	3%11=3,(int[3] ≠3),（3+1）%11=4，int[4]=3,查找成功;	2
2	2%11=2，（int[2] ≠2）,（2+1）%11=3，int[3]=2,查找成功；	2
4	4%11=4(int[4] ≠4)，（4+1）%11=5,int[5]=4,查找成功；	2
21	21%11=10(int[10] ≠21),（10+1）%11=0,int[0] ≠21，（0+1）%11=1，int[1] ≠2（1+1）%11=2int[2] ≠21，（2+1）%11=3，int[3] ≠21，（3+1）%11=4,int[4] ≠21，（4+1）%11=5,int[5] ≠21,(5+1)%11=6,int[6]=21,查找成功。	8
总共查找次数1+1+1+2+2+2+2+8=19
每个元素被查找的概率为1/8
线性搜查的ASL=19×1/8=19/8

链地址法
就是将发生冲突的元素放入同一个链表中。建立顺序表的方法也是利用Hash函数。
给定的元素
11,78,10,1,3,2,4,21
比如78%11=1,应该插入数组的1处，但是1%11=1，就插入78所在的链表中。用图示来表示就是

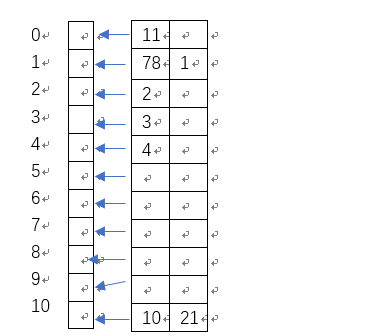
这时各元素的查找过程为，设各索引对应的头指针为T1，T2……
11:11%11=0 T0=11，查找成功
78:78%11=1 T1=78，查找成功
10:10%11=10 T10=10，查找成功
1:1%11=1 T1≠1，T1.next=1，查找成功
3:3%11=3 T3=3，查找成功
2:2%11=2 T2=2，查找成功
4:4%11=4 T4=4，查找成功
21:21%11=10 T10≠21, T10.next=21 查找成功
总共进行的查找次数为
1+1+1+2+1+1+1+2=10
每个元素被查找到的概率
1/8
ASL=10×1/8=5/4