多项式拟合
来源:同登科 《计算方法》 中国石油大学出版社 P106
*何为拟合?
从给定的函数表出发,寻找一个简单合理的函数近似表达式来拟合给定的一组数据。
这里所说的“拟合”,即不要所作的曲线完全通过所有的Σ数据点,只要求所得的近似曲线能反映数据的基本趋势。数据拟合在实际中有广泛的应用。
它的实质是离散情况下的最小平方趋近,基本思想和处理方法也具有相似性。其几何解释是:求一条曲线,使数据点均在离此曲线的上方或下方不远处。
*多项式拟合
设由实验测得函数y=f(x)在n个点x1 ,x2,...,xn的值为y1,y2,...,yn,要求这个函数的一个近似表达式。我们用一个次数低于n-1(m<n-1)的多项式φm(x)来拟合它,设
φm(x) = a0+a1x+a2x2+…+amxm (m < n -1) (1)
用最小二乘来确定系数a0,a1,…,am,令
Q(a0,a1,...,am) = ∑ni=1(φm(x)-yi)2
= ∑ni=1(a0+a1xi+a2x2i+...+amxmi-yi)2
选a0,a1,...,am,使Q(a0,a1,...,am)达到最小,将Q对ak求偏导数,并令其等于零,有

或
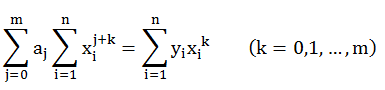 (2)
(2)
写成矩阵形式为
 (3)
(3)
上述方程组就称为多项式拟合的正规方程组,其系数阵为一对称矩阵,计算时只须将下列一些和式求出即可: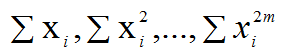 。若(3)式的系数行列式不等于零,则由(3)式可以唯一地确定系数a0,a1,...,am.
。若(3)式的系数行列式不等于零,则由(3)式可以唯一地确定系数a0,a1,...,am.
例 已知函数表如下
| xi | 1 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| yi | 2 | 7 | 8 | 10 | 11 | 11 | 10 | 9 | 8 |
试用二次多项式曲线来拟合这组数据。
解: 设二次多项式为φ(x) = a0+a1x+a2x2,为了得到正规方程组,必须先算出以下各和:
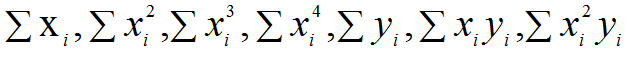
列表如下:

由上表得正规方程组为
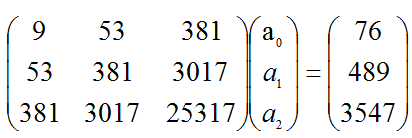
求解得 a0=-1.4597,a1=3.605,a2=-0.2676,
故φ(x)=-1.4597+3.6053x-0.2676x2.



· 10年+ .NET Coder 心语,封装的思维:从隐藏、稳定开始理解其本质意义
· .NET Core 中如何实现缓存的预热?
· 从 HTTP 原因短语缺失研究 HTTP/2 和 HTTP/3 的设计差异
· AI与.NET技术实操系列:向量存储与相似性搜索在 .NET 中的实现
· 基于Microsoft.Extensions.AI核心库实现RAG应用
· 阿里巴巴 QwQ-32B真的超越了 DeepSeek R-1吗?
· 10年+ .NET Coder 心语 ── 封装的思维:从隐藏、稳定开始理解其本质意义
· 【译】Visual Studio 中新的强大生产力特性
· 【设计模式】告别冗长if-else语句:使用策略模式优化代码结构
· 字符编码:从基础到乱码解决