树状数组
导入
定义:用数组来模拟树形结构。
用途:可以解决大部分基于区间上的更新以及求和问题。
树状数组的优点和缺点:
修改和查询的复杂度都是O(logN),而且相比线段树系数要少很多,比传统数组要快,而且容易写。
缺点是遇到复杂的区间问题还是不能解决,功能还是有限
树状数组
一、树状数组介绍
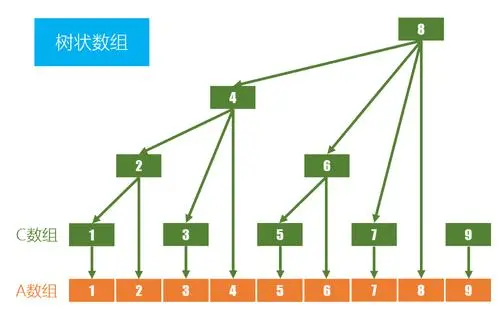
- C[1] = A[1];
- C[2] = A[1] + A[2];
- C[3] = A[3];
- C[4] = A[1] + A[2] + A[3] + A[4];
- C[5] = A[5];
- C[6] = A[5] + A[6];
- C[7] = A[7];
- C[8] = A[1] + A[2] + A[3] + A[4] + A[5] + A[6] + A[7] + A[8];
可以发现,这颗树是有规律的
C[i] = A[i - 2k+1] + A[i - 2k+2] + ... + A[i](k为i的二进制中从最低位到高位连续零的长度)
这个怎么实现求和呢,比如我们要找前7项和,那么应该是SUM = C[7] + C[6] + C[4];
而根据上面的式子,容易的出SUMi = C[i] + C[i-2k1] + C[(i - 2k1) - 2k2] + .....;
其实树状数组就是一个二进制上面的应用。
引理:2^k = i&(-i);
证明:
这里利用的负数的存储特性,负数是以补码存储的,对于整数运算 x&(-x)有:
1> 当x为0时,即 0 & 0,结果为0;
2>当x为2的m次方时,x的二进制表示中只有一位是1(从右往左的第m+1位),其右边有m位0,故x取反加1后,从右到左第有m个0,第m+1位及其左边全是1。这样,x& (-x) 得到的就是x。
3>当x不为2的m次方时
●当x为奇数,最后一位为1,取反加1没有进位,故x和-x除最后一位外前面的位正好相反,按位与结果为0。结果为1。
●当x为偶数,实际上就是把x用一个奇数左移k位。这时,x的二进制表示最右边有k个0,从右往左第k+1位为1。当对x取反时,最右边的k位0变成1,第k+1位变为0;再加1,最右边的k位就又变成了0,第k+1位因为进位的关系变成了1。左边的位因为没有进位,正好和x原来对应的位上的值相反。二者按位与,得到:第k+1位上为1,左边右边都为0。结果为2^k。
综上:x&(-x),当x为0时结果为0;x为奇数时,结果为1;x为偶数时,结果为x中2的最大次方的因子。
二、如何建立树状数组
已知:C[i] = A[i - 2k+1] + A[i - 2k+2] + ... + A[i]。
所以更新某个A[i]的值,则会影响到所有包含有A[i]位置。(这一点很重要)
代码:
三、常见更新、查询
1.单点更新、单点查询
传统数组可做
2.单点更新、区间查询
#include<bits/stdc++.h> #define N 100000 #define lowbit(x) x&-x using namespace std; int n,m; int a[N],c[N]; void change(int x,int y) //修改,使所有包含x的c[i]的值加上y { while(x<=n) { c[x]+=y; x+=lowbit(x); } } int sum(int x) // 求和 { int ans=0; while(x>0) { ans+=c[x]; x-=lowbit(x); } return ans; } int main() { cin>>n; for(int i=1;i<=n;i++) { scanf("%d",&a[i]); change(i,a[i]); } int m; cin>>m; for(int i=1;i<=m;i++) { int x; scanf("%d",&x); if(x==1) //单点修改 { int y,z; scanf("%d%d",&y,&z); change(y,z); } else { //区间查询 int l,r; scanf("%d%d",&l,&r); printf("%d\n",sum(r)-sum(l-1)); } } return 0; }
3.区间更新、单点查询
如果是像上面的树状数组来说,就必须把x-y区间内每个值都更新,这样的复杂度肯定是不行的,这个时候,就不能再用数据的值建树了,这里我们引入差分,利用差分建树。
假设我们规定D[0] = 0;
则有 D[i] = Σij = 1tr[j];(tr[j] = D[j] - D[j-1]),即前面i项的差值和,例如对于下面这个数组
- D[] = 1 2 3 5 6 9
- tr[] = 1 1 1 2 1 3
如果我们把[2,5]区间内值加上2,则变成了
- D[] = 1 4 5 7 8 9
- tr[] = 1 3 1 2 1 1
所以我们就可以利用这个性质对tr[]数组建立树状数组,代码与4类似。
4.区间更新、区间查询
上面我们说的差值建树状数组,得到的是某个点的值,那如果我既要区间更新,又要区间查询怎么办。这里我们还是利用差分,由上面可知
∑ni = 1D[i] = ∑ni = 1 ∑ij = 1tr[j];
则D[1]+D[2]+...+D[n]
= (tr[1]) + (tr[1]+D[2]) + ... + (t[1]+tr[2]+...+tr[n])
= n*tr[1] + (n-1)*tr[2] +... +tr[n]
= n * t(r[1]+tr[2]+...+tr[n]) - (1*tr[2]+...+(n-1)*tr[n])
所以上式可以变为∑ni = 1D[i] = n*∑ni = 1tr[i] - ∑ni = 1( tr[i]*(i-1) );
#include<bits/stdc++.h> #define N 1000010 #define LL long long using namespace std; int n, m; int a[N]; LL tr[N], tri[N]; //tr[]数组是原始数组的差分数组d[i]的树状数组 //tri[]数组是原始数组的差分数组乘以i即i*d[i]的树状数组 int lowbit(int x) { return x & -x; } void add(LL c[], int x, int v) { for (int i = x; i <= n; i += lowbit(i)) c[i] += v; } LL query(LL c[], int x) { LL res = 0; for (int i = x; i; i -= lowbit(i)) res += c[i]; return res; } LL get_sum(int x) { return query(tr, x) * (x + 1) - query(tri, x); } int main() { scanf("%d%d", &n, &m); for (int i = 1; i <= n; ++i) scanf("%d", &a[i]); for (int i = 1; i <= n; ++i) tr[i] = a[i] - a[i - 1], tri[i] = tr[i] * i; for (int x = 1; x <= n; ++x) for (int i = x - 1; i >= x - lowbit(x) + 1; i -= lowbit(i)) tr[x] += tr[i], tri[x] += tri[i]; while (m--) { char op[2]; int l, r, c; scanf("%s", op); if (op[0] == 'Q') { scanf("%d%d", &l, &r); printf("%lld\n", get_sum(r) - get_sum(l - 1)); } else { scanf("%d%d%d", &l, &r, &c); add(tr, l, c), add(tr, r + 1, -c); add(tri, l, l * c), add(tri, r + 1, (r + 1) * -c); } } return 0; }

