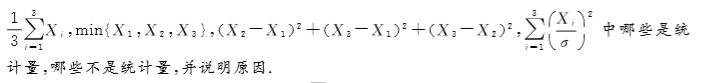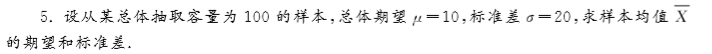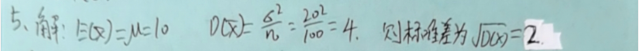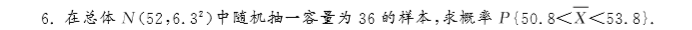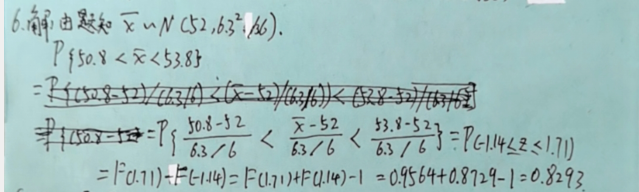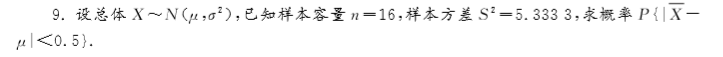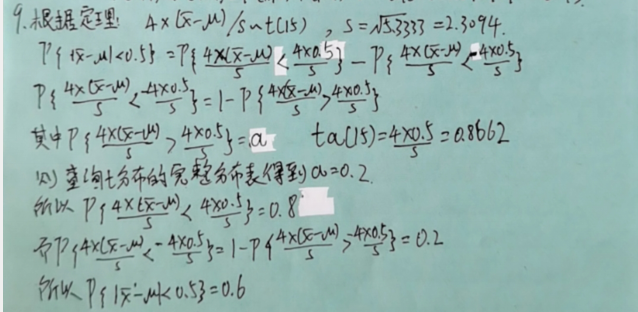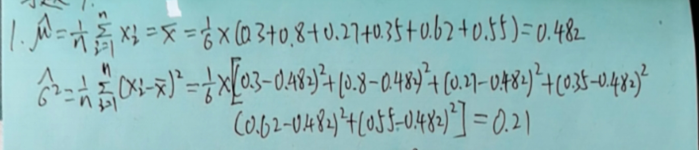概率论与数理统计 习题题目及答案(总)
一、
2.设A , B , C表示3个随机事件,用A , B , C 的运算关系表示下列各事件.
(1) A , B , C 都发生;
(2) A , B , C 都不发生;
(3) A 发生, B 与 C 不发生;
(4) A , B , C 中至少有一个发生;
(5) A , B , C 中恰好有2个发生;
(6) A , B , C 中不多于一个发生.

5.从10个同类产品(其中有8个正品, 2个次品)中任意抽取3个,试求:
(1)抽出的3个产品中都是正品的概率;
(2)至少1个是次品的概率;
(3)仅有1个次品的概率.


8.设A , B , C三个事件,且P ( A )= P ( B )= P ( C )=1/4, P ( AB )= P ( BC )=0, P ( AC )=1/8,求A , B , C至少有一个发生的概率.

10.口袋中有10个球,分别标有号码1到10.现从中不放回地任取3个,记下取出球的号码,试求:
(1)最小号码为5的概率;
(2)最大号码为5的概率.

12.12.甲、乙两轮船驶向一个不能同时停泊2艘轮船的码头,它们在一昼夜内到达的时刻 是等可能的,如果甲船的停泊时间是1小时,乙船的停泊时间是2小时,求它们中任何一艘 船都不需要等候码头空出的概率.

14.已知P ( A )=1/4, P ( B | A )=1/3, P ( A | B )=1/2,求P ( A ∪ B ).
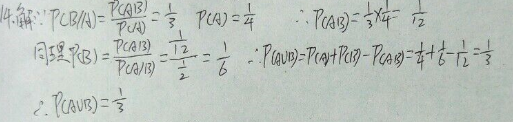
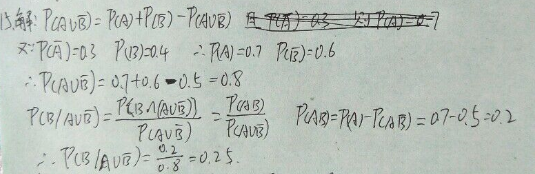
24.事件A与 B相互独立, P ( A )=0. 4, P ( A ∪ B )=0. 7,求P ( B ).
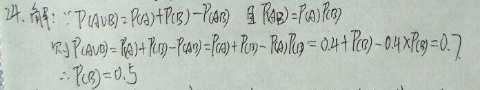
33.甲、乙、丙3个运动员自离球门25码处踢进球的概率依次为0. 5, 0. 7, 0. 6,设3人 各在离球门25码处踢一球,设各人进球与否相互独立,求:
(1)恰好有1人进球的概率;
(2)恰好有2人进球的概率;
(3)至少有1人进球的概率.


二、
1.已知随机变量只能取0, 1, 2, 3这4个值,其相应的概率依次为1/ 2c ,3/ 4c ,5/ 8c ,1/ 8c ,求常数c的值。
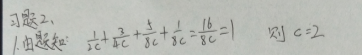
2.( 1)一袋中装有5个球,编号为1, 2, 3, 4, 5.在袋中同时取3个,以X表示取出的3个球中的最大号码,
写出随机变量X 的分布列.
( 2)将一颗骰子抛掷两次,以 Y 表示两次中得到的小的点数,试求 Y的分布列.

5.设随机变量X ~ P ( λ ),已知P { X =2}= P { X =3},求P { X =4}.
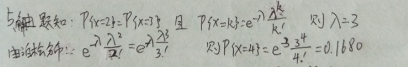
9.设离散型随机变量的分布列为P { X =0}=0. 5, P { X =1}=0. 3, P { X =3}=0. 2,
求:( 1) X的分布函数;( 2) F ( 1. 5).


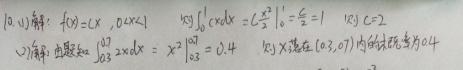
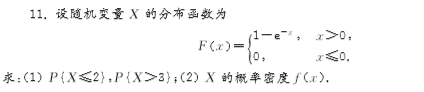
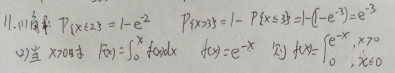
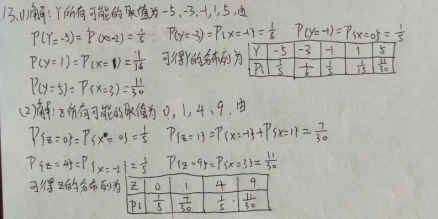

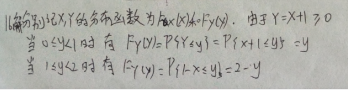

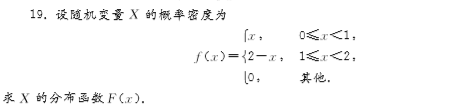
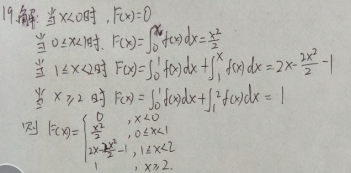

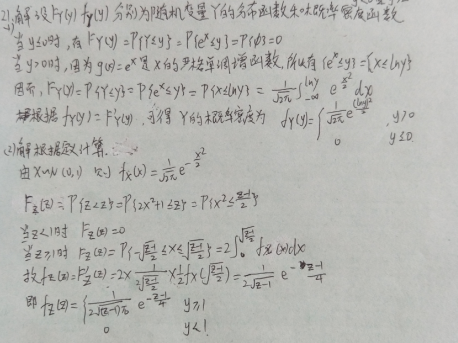
三、
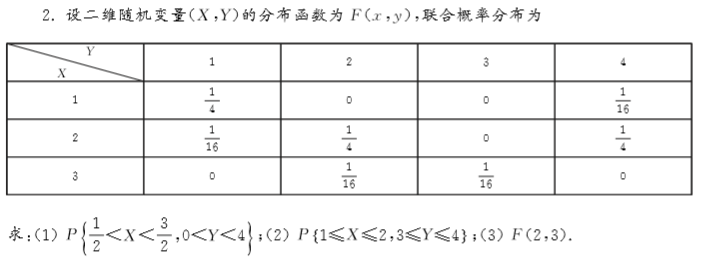
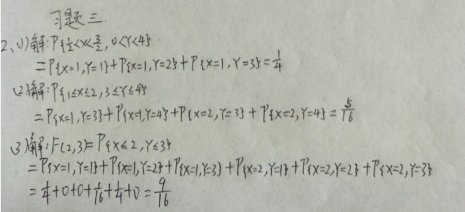
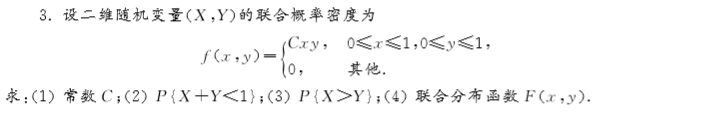

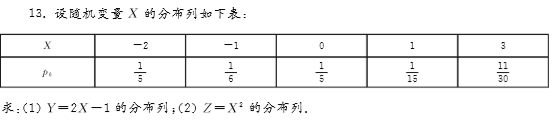
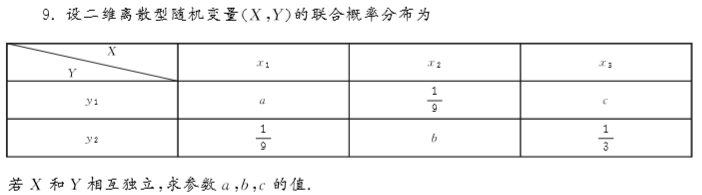
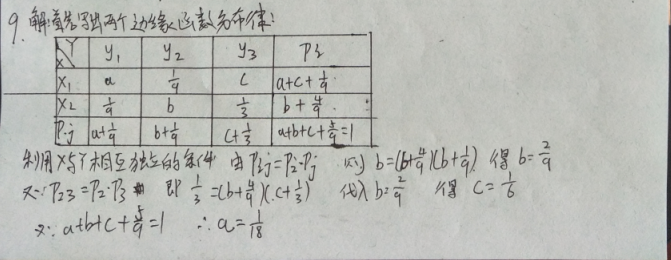
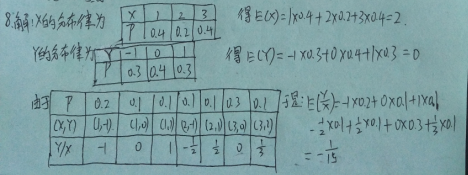
5.求第1题中二维随机变量( X , Y )关于X和 Y的边缘分布列.
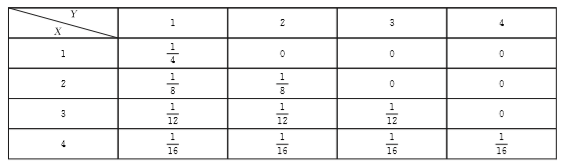


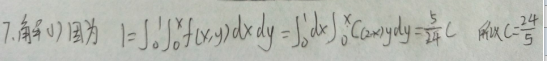
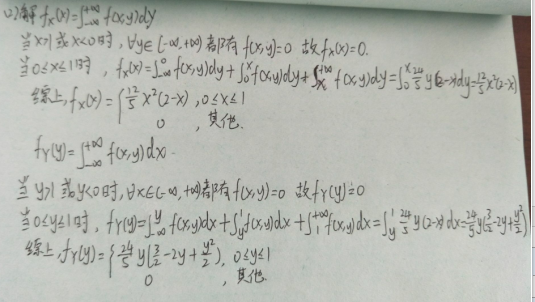

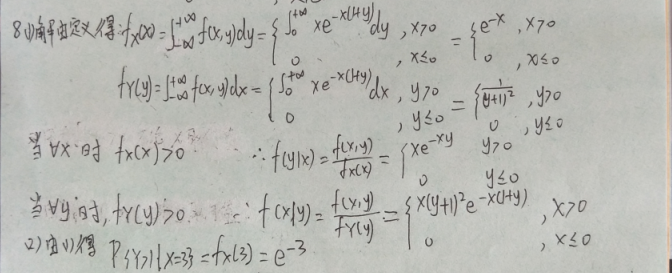


四、
1.设盒中有5个球,其中2个白球, 3个黑球,从中随意抽取3个球.记X为抽取到的白球数,求E ( X ).
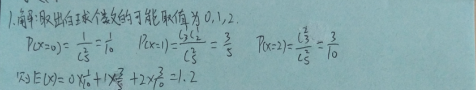
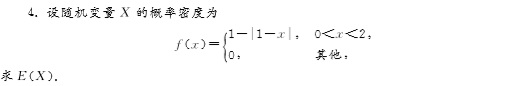
![]()

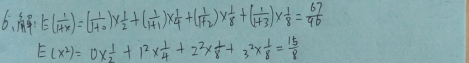
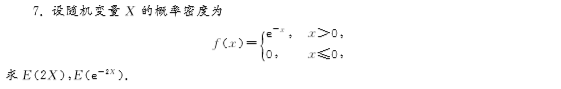
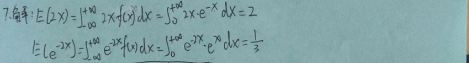
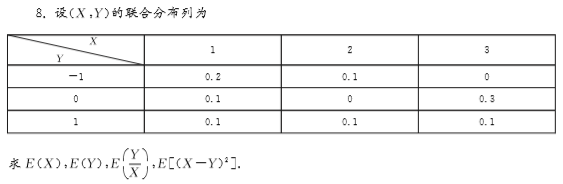

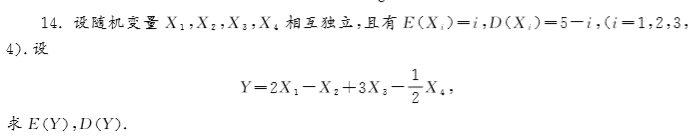
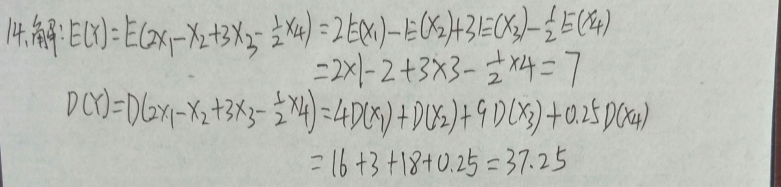
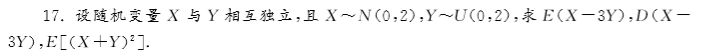
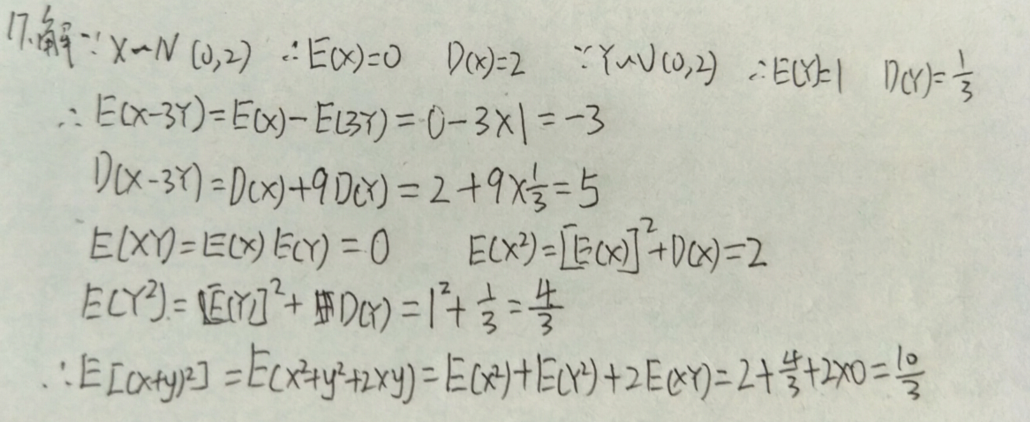


六七、
![]()