基本的数据结构为无向图。但是考虑到地铁站太多,如果把地铁站都作为此无向图中的顶点,生成的图太过复杂,这样生成最短路径算法效率肯定也不高。所以我们的思路是无向图中只保留换乘站,而两个换乘站之间的普通车站就退化成边。
基于这个思路,设计的数据结构为
| 线路号 | 开始换乘站 | 结束换乘站 | 中间普通车站数组 |
其中换乘站和普通站的数据结构相同,都是如下结构体
struct{
int 编号;
int 里程;
}station;
具体解释一下:
int 编号:在获得地铁线路信息后,为了日后编写代码方便,我们需要将所有的站点进行编码,就用熟悉的十进制就好。
要注意的是,换乘站是要作为顶点出现在无向图的。所以规整所有的换乘站,使其从0开始编号,0,1,2,3,4……n-1,这样就获得了无向图中顶点个数n了。
在换乘站分配编号之后,再开始分配普通站的编号,比如我们可以预留大一点的空间给换乘站,使普通站从100开始编号。
int 里程:具体到每一条地铁线上,这个里程指的是当前站到下一站的距离。这条地铁线上的每一个站都存储着到下一个站的距离,这样就能完整的保存整条地铁线的距离信息了。
从北京地铁线上截取一角:
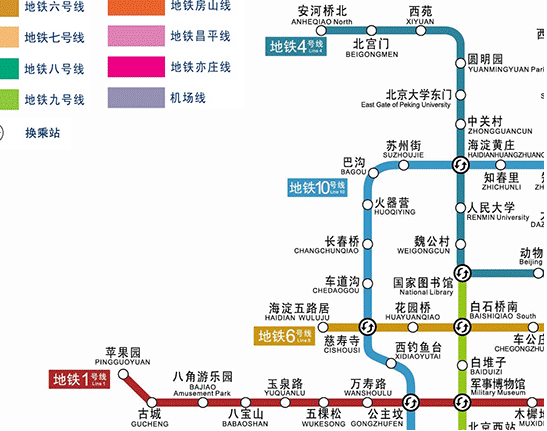
现在以这个为例具体到我们设计的数据结构上。我们就有如下的数组:
| 1号线 | -1 | 公主坟 | 苹果园 | 古城 | 八角游乐园 | 八宝山 | 玉泉路 | 五棵松 | 万寿路 |
| 10号线 | 公主坟 | 海淀黄庄 | 西钓鱼台 | 慈寿寺 | 车道沟 | 长春桥 | 火器营 | 巴沟 | 苏州街 |
-1代表无换乘站
在具体实现时,公主坟代表的就是换乘站,数据结构为struct station{ int 0,int 5 }(假设换乘站编号从公主坟开始,从公主坟到军事博物馆的里程为5)
苹果园代表的就是普通站,数据结构为struct station{int 101,int 10}(假设普通站编号从苹果园开始,从苹果园到古城的里程为10)
根据此数据结构,设计算法思路。算法基础:用Dijkstra可以求出无向图中从某一个顶点到其他所有结点的最短路径。
用户输入起点和终点。这里我们用编号代替。起点:int start; 终点:int end;
我们可以分为4种情况:
1.起点和终点都是普通车站
2.起点是换乘车站,终点是普通车站
3.起点是普通车站,终点是换乘车站
4.起点和终点都是换乘车站。
我们先考虑第一种情况。
现在的情况是假设所有的地铁信息已经转换成前面所定义的数据结构了,我们有的是包含所有信息的数组。算法步骤如下:
步骤1:根据start和end这两个编号遍历上述数组,得到以下结构:
| 几号线 | 开始换乘站 | 结束换乘站 | …… | start | …… |
| 几号线 | 开始换乘站 | 结束换乘站 | …… | end | …… |
用车站编号代替举例:
| 1 | 0 | 1 | …… | start | …… |
| 2 | 3 | 4 | …… | end | …… |
表明start在0,1换乘站之间,end在3,4换乘站之间。
步骤2:先设源点为0,运用Dijkstra算法,计算出从0到3,从0到4的最短路径,为m1,m2;
再改变源点为1,运行Dijkstra算法,计算出从1到3,从1到4的最短路径,为m3,m4;
步骤3:根据车站结构体中的另一个元素int 里程,计算从start到0的里程x1,start到1的里程x2,end到3的里程x3,end到4的里程x4。
步骤4:对于步骤2中的4条路径0——>3,0——>4,1——>3,1——>4,计算从开始站到终点站的里程。
对于路径0——>3,里程=m1 + x1 + x3;
对于路径0——>4,里程=m2 + x1 + x4;
对于路径1——>3,里程=m3 + x2 + x3;
对于路径1——>4,里程=m4 + x2 + x4;
根据最小里程,选择最佳路径。
现在考虑其他三种情况,只需要做一点的修改,例如情况2,起点为换乘站,那么只需要在步骤2中设源点为strat,只需要运行一次Dijkstra算法计算到终点站左右两边的换乘站就行。
上述步骤是在无向图已经创建好的条件下。无向图也是根据地铁信息填充的结构数组创建的。顶点个数为换乘站个数,顶点的边嘛,根据上面的例子,就有两条边,从0到1,从3到4,。



