博雅大数据机器学习十讲第五讲

聚类：物以类聚，人以群分

• 假设\(f(x)\)为多元函数，如果对任意\(t\in[0,1]\)，均满足：

\[f(tx_1+(1-t)x_2)\le tf(x_1)+(1-t)f(x_2) \]

则称\(f(x)\)为凸函数

• \(Jensen\)不等式：如果\(f\)是凸函数，\(X\)是随机变量，则：\(f(E[X])\le E[f(X)]\)
• \(Jensen\)不等式另一种描述

\[f(\sum^n_{i=1}a_ix_i)\le \sum^n_{i=1}a_if(x_i) \]

• 取等号的条件是：\(f(x_i)\)是常量

• 聚类的本质：将数据集中相似的样本进行分组的过程

• 每个组称为一个簇\((cluster)\)每个簇的样本对应一个潜在的类别

• 样本没有类别标签，一种典型的无监督学习方法

• 这些簇满足以下两个条件

  • 相同簇的样本之间距离较近
  • 不同簇的样本之间距离较远

• 聚类方法：层次聚类、\(K-Means\)、谱聚类等

• \(K-Means\)最初起源于信号处理，是一种比较流行的聚类方法

• 数据集为\(\{x_i\}_{i=1}^n\)，将样本划分为\(k\)个簇，每个簇中心为\(c_j(1\le j \le k)\)

• 优化目标：最小化所有样本点到所属簇中心的距离平方和

\[J(r,c)=\sum^k_{j=1}\sum^n_{i=1}r_{ij}||x_i-c_j||^2_2 \]

• 其中\(r_{ij}\in \{0,1\}\)，若样本\(x_i\)被划分到簇\(k\)中，那么\(r_{ij}=1\)，且对于\(j\neq k\)，有\(r_{ij} = 0\)，\(\sum ^k_{j=1}r_{ij} = 1\)

• 模型：\(\min\limits_{r,c}J(r,c)=\sum^k_{j=1}\sum^n_{i=1}r_{ij}||x_i-c_j||^2_2\)

• 交替迭代法：

  • 固定\(c\)，优化\(r\)
  • 固定\(r\)，优化\(c\)

• 优化目标：\(J(r)=\sum^n_{j=1}\sum^k_{i=1}r_{ij}||x_i-c_j||^2_2=\sum^n_{i=1}J_i(r_i)\)

• 算法流程：

  • 随机选择\(k\)个点作为初始中心
  • \(Repeat\)：
    • 将每个样本指派到最近的中心，形成\(k\)个类
    • 重新计算每个类的中心为该类样本均值
  • 直到中心不发生变化

高斯混合模型(GMM)

• 假设数据集\(\{x_i\}^n_{i=1}\)从\(k\)个高斯模型中生成\(\{N(x|\mu_j,\sum_j)\}^k_{j=1}\)，样本来自第\(j\)个高斯的概率为\(\pi_j，\sum^k_{j=1}\pi_j=1\)，记\(\theta = \{\mu,\sum,\pi\}\)
• \(r_{ij}\)表示\(x_i\)来自高斯\(j\)的概率，\(r_{ij}\in[0,1]，\sum^k_{j=1}r_{ij}=1\)
• \(p(x_i)=\sum^k_{j=1}\pi_jN(x_i|\mu_j,\sum_j)\)
• 优化目标为最大化对数似然函数：

\[LL(\theta)=\sum^n_{i=1}ln(\sum^k_{j=1}\pi_jN(x_i|\mu_j,\sum_j)) \]

EM算法

• 假设数据集为\({x_i}^n_{i=1}\)，隐含变量为\(\{z_i\}^n_{i=1}，z_i\in\{1,2,...,k\}\)模型参数为\(\theta\)

• 似然函数\(LL(\theta)=\sum^n_{i=1}ln(\sum^k_{j=1}p(x_i,z_i|\theta))\)

• 算法流程：

  • 初始化参数\(\theta^{(0)}\)
  • 不断重复以下两步直到收敛：
    • \((E-step)\)求解\(L(\theta)\)的下界函数，等价于求\(Q\)函数：\(Q_i(z_i|\theta^{(t)})=p(z_i|x_i,\theta^{(t)})\)
    • \((M-step)\)下界函数最大化\(\theta^{(t+1)}=argmax_\theta\sum^n_{i=1}\sum^k_{j=1}q_i(z_i|\theta^{(t)})ln\frac{P(x_i,z_i|\theta)}{Q_i(z_i|\theta^{(t)})}\)

案例：

假设我们使用欧式距离计算样本到中心的距离。对于样本 \(d\) 维样本 \(\mathbf{x}\) 到中心 \(\mathbf{c}\) 的欧式距离计算公式为：

\[\text{dist}(\mathbf{x},\mathbf{c}) = \sqrt{\sum_{i=1}^{d} (x_i-c_i)^2} = \Vert \mathbf{x} - \mathbf{c}\Vert_2. \]

使用最简单的方式来实现，先用一个函数 point_dist 计算一个样本到中心的距离。这里我们使用 Numpy 的线性代数模块 linalg 中的 norm 方法。

import numpy as np
def point_dist(x,c): #定义距离计算函数
    return np.linalg.norm(x-c)
#然后使用 iterrows 方法遍历样本计算样本到中心的距离，定义 k_means_iterrows 方法实现 K-Means 算法。
def k_means1(X,k):
    centers = X.sample(k).values #从数据集随机选择 K 个样本作为初始化的类中心，k 行 d 列
    X_labels = np.zeros(len(X)) #样本的类别
    error = 10e10
    while error > 1e-6:
        for i,x in X.iterrows():#指派样本类标签
            X_labels[i] = np.argmin([point_dist(x,centers[i,:]) for i in range(k)])
        centers_pre = centers
        centers = X.groupby(X_labels).mean().values #更新样本均值，即类中心
        error = np.linalg.norm(centers_pre - centers)#计算error
    return X_labels, centers
#用一个简单的随机数据集来测试时间性能。Sklearn 中的 datasets 模块的 make_blobs 函数能够自动生成一些供测试聚类算法的随机数据集。它能够根据输入的参数生成数据集和对应的类标签。
from sklearn import datasets
import pandas as pd
X, y = datasets.make_blobs(n_samples=5000, n_features=8, cluster_std = 0.5,centers=3,random_state=99)
X_df = pd.DataFrame(X)
#在该数据集上用我们实现的 k_means1 方法运行 K-Means 聚类。使用 iPython 提供的魔法命令 %time 记录运行时间。
%time labels,centers = k_means1(X_df,3) # for 循环
#提高运算效率，可以使用 DataFrame 的 apply 函数，它可以对数据框中的每一行执行一个复杂的函数。在我们的例子中，是计算每一行与每一个中心的距离。
def k_means2(X,k):
    #初始化 K 个中心，从原始数据中选择样本
    centers = X.sample(k).values
    X_labels = np.zeros(len(X)) #样本的类别
    error = 10e10
    while error > 1e-6:
        #********#
        X_labels = X.apply(lambda r : np.argmin([point_dist(r,centers[i,:]) for i in range(k)]),axis=1)
        centers_pre = centers
        centers = X.groupby(X_labels).mean().values #更新样本均值，即类中心
        error = np.linalg.norm(centers_pre - centers)#计算error
    return X_labels, centers
%time labels,centers = k_means2(X_df,3) # apply 运算

数据集表示成 \(n \times d\) 矩阵 \(\mathbf{X}\)，其中 \(n\) 为样本数量，\(d\) 为样本的维度。 \(k\) 个聚类中心表示成 \(k \times d\) 矩阵 \(\mathbf{C}\)，\(\mathbf{C}\) 每一行表示一个聚类中心。样本到 \(k\) 个中心的距离表示成 \(n \times k\) 矩阵 \(\mathbf{D}\)。

已经聚类中心，计算样本到中心距离，并将样本划分到距离最小的类。

使用 Numpy 实现上述计算流程的代码为：

for i in range(k):

    D[:,i] = np.sqrt(np.sum(np.square(X - C[i,:]),axis=1))
    
labels = np.argmin(D,axis=1)

得到样本的类标签后，聚类中心的更新流程为：1）根据类标签对样本进行分组；2）将聚类中心更新为每一组样本的均值。Python 实现的代码为：

 C = X.groupby(labels).mean().values

现在我们更新 K-Means 算法的实现，函数名为 k_means。

import pandas as pd
import numpy as np


def k_means(X, k):
    C = X.sample(k).values  # 从数据集随机选择 K 个样本作为初始化的类中心，k 行 d 列
    X_labels = np.zeros(len(X))  # 记录样本的类别
    error = 10e10  # 停止迭代的阈值
    while error > 1e-6:
        D = np.zeros((len(X), k))  # 样本到每一个中心的距离，n 行 k 列
        for i in range(k):
            D[:, i] = np.sqrt(np.sum(np.square(X - C[i, :]), axis=1))
        labels = np.argmin(D, axis=1)
        C_pre = C

        temp_C = X.groupby(labels).mean()  # 更新样本均值，即类中心
        C = np.zeros((k, X.shape[1]))
        for i in temp_C.index:
            C[i, :] = temp_C.loc[i, :].values

        if C.shape == C_pre.shape:
            error = np.linalg.norm(C_pre - C)  # 计算error
        else:
            print(C.shape, C_pre.shape)
    return labels, C
%time labels,centers = k_means(X_df,3) # 矩阵运算
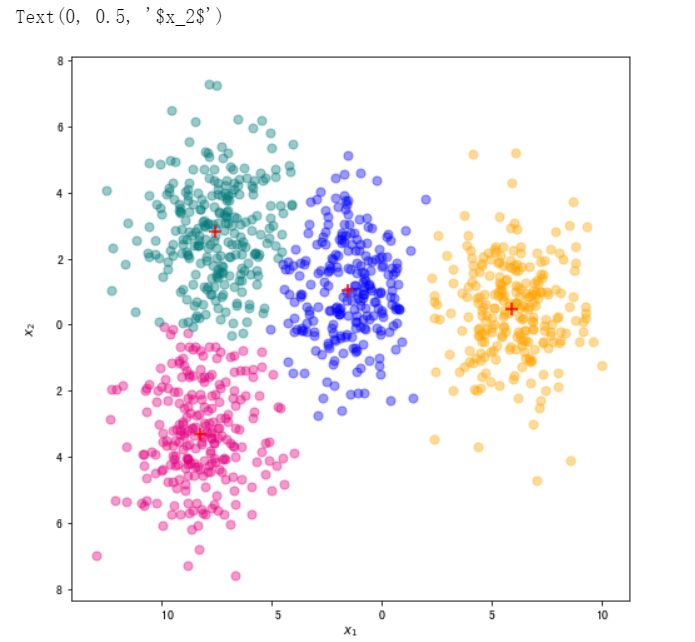
#下面我们使用一份随机生成的二维数据集，使用我们上一小节实现的 k_means 完成聚类，然后使用不同颜色标注不同类的样本以及类中心。
color_dict = {0:"#E4007F",1:"#007979",2:"blue",3:"orange"} #洋红，深绿，蓝色，橘色
from sklearn import datasets
import matplotlib.pyplot as plt
import pandas as pd
%matplotlib inline
X, y = datasets.make_blobs(n_samples=1000, n_features=2, cluster_std = 1.5,centers=4,random_state=999)
X_df = pd.DataFrame(X,columns=["x1","x2"])
labels,centers= k_means(X_df,4)
fig, ax = plt.subplots(figsize=(8, 8)) #设置图片大小
for i in range(len(centers)):
    ax.scatter(X_df[labels == i]["x1"],X_df[labels == i]["x2"],color=color_dict[i],s=50,alpha=0.4)
    ax.scatter(centers[int(i),0],centers[int(i),1],color="r",s=100,marker="+")
plt.xlabel("$x_1$")
plt.ylabel("$x_2$")

# 要动态展示 K-Means 聚类过程，我们需要在每一步迭代中记录每一个类的中心，以及每一个类的样本集合。创建 k_means_steps，在完成聚类的同时，将每一步迭代的每类样本和中心返回。
def k_means_steps(X, k):
    # 初始化 K 个中心，从原始数据中选择样本
    # ********#
    samples_list = []  # 记录每一个中间迭代中每一类样本
    centers_list = []  # 记录每一个中间迭代中每一类样本中心
    # ********#
    C = X.sample(k).values
    labels = np.zeros(len(X))  # 样本的类别
    error = 10e10
    while (error > 1e-6):
        D = np.zeros((len(X), k))  # 样本到每一个中心的距离
        for i in range(k):
            D[:, i] = np.sqrt(np.sum(np.square(X - C[i, :]), axis=1))
        labels = np.argmin(D, axis=1)
        C_pre = C
        C = X.groupby(labels).mean().values  # 更新样本均值，即类中心
        # ********# 记录当前迭代地每一类的样本集合和中心
        samples, centers2 = [], []
        for i in range(k):
            samples.append(X[labels == i])
            centers2.append(C[i, :])

        samples_list.append(samples)
        centers_list.append(centers2)
        # ********#
        if C.shape == C_pre.shape:
            error = np.linalg.norm(C_pre - C)  # 计算error
        else:
            print(C.shape, C_pre.shape)
    return labels, C, samples_list, centers_list  # ********# 返回最终的聚类结果，聚类中心，每一步的聚类结果和聚类中心


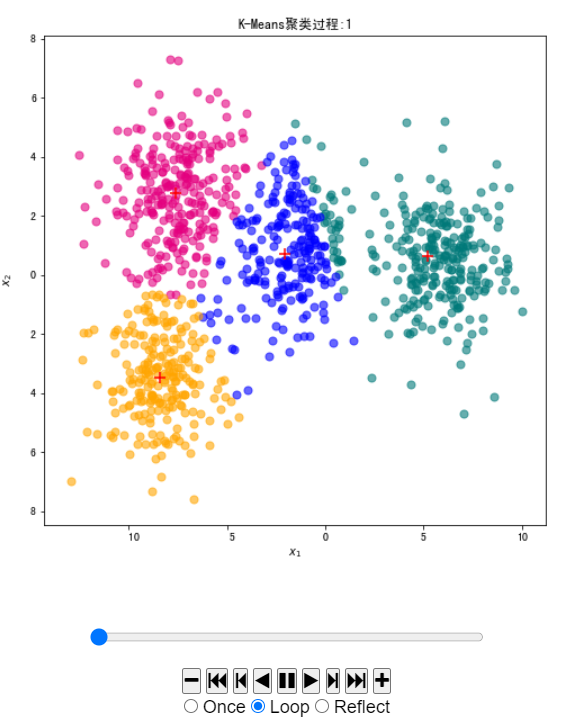
# 我们可以借助 matplotlib.animation 动画模块来实现下面的 init_draw 函数是动画最开始时绘制的内容，包含数据。update_draw 则是每次更新的内容。
labels, centers, samples_list, centers_list = k_means_steps(X_df, 4)
fig, ax = plt.subplots(figsize=(8, 8))

samples_obj = []
centers_obj = []


def init_draw():  # 展现样本数据
    ax.set_title("K-Means聚类过程:")
    for i in range(len(centers)):
        samples_obj.append(
            ax.scatter(samples_list[0][i]["x1"], samples_list[0][i]["x2"], color=color_dict[i], s=50, alpha=0.6))
        centers_obj.append(ax.scatter(centers_list[0][i][0], centers_list[0][i][1], color="r", s=100, marker="+"))
    plt.xlabel("$x_1$")
    plt.ylabel("$x_2$")


def update_draw(t):  # 实现动画中每一帧的绘制函数，i为第几帧
    ax.set_title("K-Means聚类过程:" + str(t))
    samples, centers = samples_list[t], centers_list[t]
    for i in range(len(centers)):
        samples_obj[i].set_offsets(samples[i])
        centers_obj[i].set_offsets(centers[i])
    plt.close()


# 演示决策面动态变化
import matplotlib.animation as animation
from IPython.display import HTML

animator = animation.FuncAnimation(fig, update_draw, frames=range(1, len(centers_list)), init_func=init_draw,
                                   interval=2000)
HTML(animator.to_jshtml())

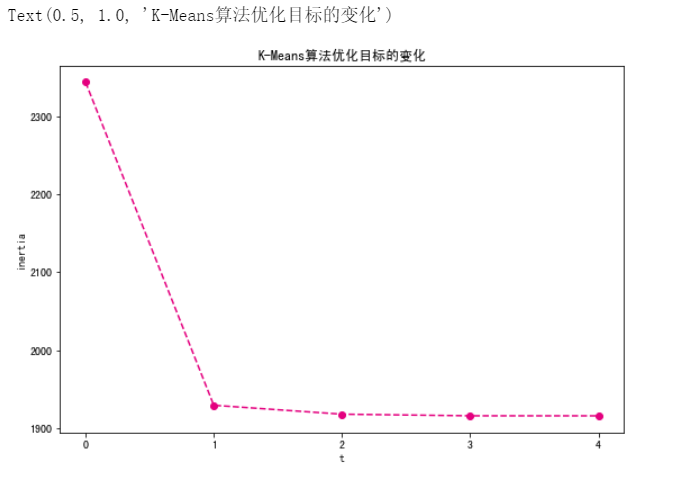
# 我们来查看随着迭代的进行，K-Means聚类模型的优化目标，即失真度量  JJ  的变化。对算法进行修改，记录每一步的失真度量。
import pandas as pd
import numpy as np


def k_means_inertia(X, k):
    # 初始化 K 个中心，从原始数据中选择样本
    C = X.sample(k).values
    labels = np.zeros(len(X))  # 样本的类别
    inertia_list = []  # *****记录优化目标****#
    error = 10e10
    while (error > 1e-6):
        D = np.zeros((len(X), k))  # 样本到每一个中心的距离
        for i in range(k):
            D[:, i] = np.sqrt(np.sum(np.square(X - C[i, :]), axis=1))
        labels = np.argmin(D, axis=1)

        inertia_list.append(np.square(np.min(D, axis=1)).sum())  # ****记录当前步骤的失真度量****#

        C_pre = C
        temp_C = X.groupby(labels).mean()  # 更新样本均值，即类中心
        C = np.zeros((k, X.shape[1]))
        for i in range(len(temp_C)):
            C[i, :] = temp_C.loc[i, :].values
        if C.shape == C_pre.shape:
            error = np.linalg.norm(C_pre - C)  # 计算error
    return labels, C, inertia_list


# 在随机数据上进行聚类，并将失真度量的变化以折线图的形式绘制出来。
X, y = datasets.make_blobs(n_samples=1000, n_features=2, cluster_std=1, centers=3, random_state=99)
X_df = pd.DataFrame(X, columns=["x1", "x2"])
labels, centers, inertia_list = k_means_inertia(X_df, 3)
fig, ax = plt.subplots(figsize=(9, 6))  # 设置图片大小
t = range(len(inertia_list))
plt.plot(t, inertia_list, c="#E4007F", marker="o", linestyle='dashed')
plt.xlabel("t")
plt.ylabel("inertia")
plt.xticks(t)
plt.title("K-Means算法优化目标的变化")

我们先加载一张测试图片，将图片打印出来。使用 PIL.Image.open 方法来打开图片，然后使用 matplotlib 中的 imshow 方法将图片可视化。

from PIL import Image

fig, ax = plt.subplots(figsize=(6, 5))  # 设置图片大小
path = './input/timg.jpg'
img = Image.open(path)
plt.imshow(img)
plt.box(False)  # 去掉边框
plt.axis("off")  # 不显示坐标轴
# 将一张图片转换成表格形式。每一行为一个像素，三列分别为像素的 R，B，G取值。获取图片的每一个像素  (i,j)(i,j)  的 RBG 值可以使用 Image 类的 getpixel 方法。
import pandas as pd


def image_dataframe(image):  # 将图片转换成DataFrame,每个像素对应每一行，每一行包括三列
    rbg_values = []
    for i in range(image.size[0]):
        for j in range(image.size[1]):
            x, y, z = image.getpixel((i, j))  # 获取图片的每一个像素  (i,j)(i,j)  的 RBG 值
            rbg_values.append([x, y, z])
    return pd.DataFrame(rbg_values, columns=["R", "B", "G"]), img.size[0], img.size[1]


img_df, m, n = image_dataframe(img)
img_df.head()
print(m, n, m * n, len(img_df))
labels, _ = k_means(img_df, 2)
# 将生成的灰度图可视化，对图像可视化使用 plt.imshow 方法。
fig, ax = plt.subplots(figsize=(6, 5))  # 设置图片大小
labels = labels.reshape((m, n))
pic_new = Image.new("L", (m, n))
# 根据类别向图片中添加灰度值
for i in range(m):
    for j in range(n):
        pic_new.putpixel((i, j), int(256 / (labels[i][j] + 1)))
plt.imshow(pic_new)
plt.box(False)  # 去掉边框
plt.axis("off")  # 不显示坐标轴


# 实现一个函数 img_from_labels ，将像素聚类类别标签，转换成一张灰度图。
def img_from_labels(labels, m, n):
    labels = labels.reshape((m, n))
    pic_new = Image.new("L", (m, n))
    # 根据类别向图片中添加灰度值
    for i in range(m):
        for j in range(n):
            pic_new.putpixel((i, j), int(256 / (labels[i][j] + 1)))
    return pic_new


# 调整聚类数量  kk , 将聚类得到的不同的灰度图使用 Matplotlib 将生成的灰度图绘制出来。
fig, ax = plt.subplots(figsize=(18, 10))  # 设置图片大小
img = Image.open(path)  # 显示原图
plt.subplot(2, 3, 1)
plt.title("原图")
plt.imshow(img)
plt.box(False)  # 去掉边框
plt.axis("off")  # 不显示坐标轴

for i in range(2, 7):
    plt.subplot(2, 3, i)
    plt.title("k=" + str(i))
    labels, _ = k_means(img_df, i)
    pic_new = img_from_labels(labels, m, n)
    plt.imshow(pic_new)
    plt.box(False)  # 去掉边框
    plt.axis("off")  # 不显示坐标轴

本案例中我们使用首先使用三种方式实现了 K-Means 算法并对不同实现的时间性能进行了对比，结果发现向量化实现能够大大提高运行效率。然后我们使用 K-Means 算法进行图像分割，展示了不同 K 取值下生成的灰度图的变化。最后，我们使用 K-Means 在一份中文新闻数据集进行了主题聚类。

本案例使用的主要 Python 工具如下：

工具包	用途
NumPy	矩阵运算
Pandas	数据读取与预处理
Matplotlib	数据集可视化、聚类结果动画
Sklearn	中文新闻的向量化
Wordcloud	绘制聚类结果词云图