递推与记忆化搜索
内容参考书籍《算法竞赛入门到进阶》
先看一道经典题:poj1163 http://poj.org/problem?id=1163
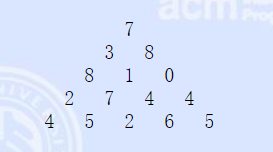
如果此题按照从上往下的方法计算,每走一步下一步就有2种选择,其复杂度为2n
那么我们从下往上算,下面给出dfs代码:
1 2 3 4 5 | int dfs(int i,int j){ if (i == n) return a[i][j];//递归到最后一行返回 return dp[i][j] = max(dfs(i+1,j),dfs(i+1,j+1))+ a[i][j];} |
从1,1开始往下走,一直到最后一行,返回,每一次取能走到该点的最大值加上该点,继续返回,代码很好理解,只是复杂度为2n
下面我们再来讲一下递推,代码如下:
1 2 3 4 5 6 7 | for (int j = 1; j <= n; ++j) dp[n][j] = a[n][j];for (int i = n-1; i >= 1; --i){ for (int j = 1; j <= i; ++j) { dp[i][j] = max(dp[i+1][j],dp[i+1][j+1]) + a[i][j]; } }cout<<dp[1][1]<<endl; |
首先是第一层循环,将三角形最下面一层全部赋值给dp,然后从下往上求解,输出dp[1][1]即是最大值。这样复杂度便只有n2
那么搜索可以做到吗?当然可以,这就是我们说的记忆化,只需要在搜索算法中加入if即可,代码如下:
1 2 3 4 5 6 | int dfs(int i,int j){ if (i == n) return a[i][j];//递归到最后一行返回 if (dp[i][j] >= 0) return dp[i][j];//记忆 return dp[i][j] = max(dfs(i+1,j),dfs(i+1,j+1))+ a[i][j];} |
这样搜索算法的复杂度也降到了n2,为什么要加这样一句话呢?我们可以发现,当我们从第2层的“3”往下走会经过“1”,计算一次从1出发的递归;从第2层的“8”往下走也会经过“1”,又重新计算了“1”出发的递归,为了避免这样的重复,使用记忆化便能避免,从而降低复杂度。
分类:
动态规划



【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】凌霞软件回馈社区,博客园 & 1Panel & Halo 联合会员上线
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 深入理解 Mybatis 分库分表执行原理
· 如何打造一个高并发系统?
· .NET Core GC压缩(compact_phase)底层原理浅谈
· 现代计算机视觉入门之:什么是图片特征编码
· .NET 9 new features-C#13新的锁类型和语义
· Spring AI + Ollama 实现 deepseek-r1 的API服务和调用
· 《HelloGitHub》第 106 期
· 数据库服务器 SQL Server 版本升级公告
· 深入理解Mybatis分库分表执行原理
· 使用 Dify + LLM 构建精确任务处理应用