树状数组(Binary Indexed Tree,BIT)

内容参考书籍《算法竞赛入门到进阶》

　　树状数组是一种用树形结构维护数组巧妙运用数的二进制特征进行检索的数据结构。

 

引入以下问题：对长度为n的数组进行以下操作

(1) 修改元素：将第x个数加上k

(2) 求和：输出区间[a,b]的和

 

前置知识：lowbit操作：非负整数n在二进制表示下最低位1及其后面的0构成的数值

例如：44的二进制为101100，则其最低位1及其后面的0为100，即4，所以lowbit(44) = 4

那么如何快速计算任意一个数的lowbit呢？

首先我们将这个数按位取反 即：101100 按位取反为 010011 ，再+1，即：010100，再与原数按位与，结果为00100 = 4

由于计算机存储的是补码(相关内容请查阅资料) ：一个数取反+1后的值就是负的这个数，即：~n+1 = -n

故，lowbit(n) = n&-n

 

树状数组的实现

那么lowbit操作有什么用呢？首先我们来看一下树状数组的结构，如下图(图片来源于Bing搜索)

 

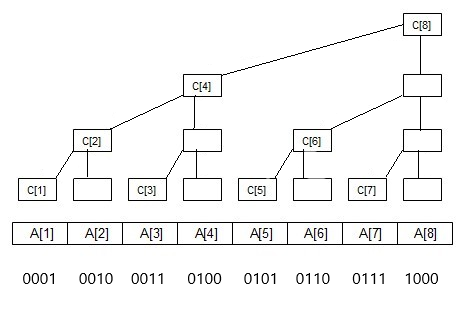
 在没学树状数组之前，我对这样的结构很困惑，为什么c[1]存储a[1]，c[2]存储a[1]+a[2]，而c[3]又存储a[3]了呢？（当时的我只能想到前缀和的算法）貌似是毫无规律的存储啊！！(难道有这种疑惑的只有我一个？？)但其实是有规律的，那就是巧妙利用二进制！！！

观察发现，只存储一个数的n其lowbit(n) = 1，例如上图中，1,3,5,7，的lowbit值均为1，而，2,6，lowbit值为2，4的值为4，8为8，可以得出结论，c[i]结点覆盖的长度就是lowbit(i)

进一步观察发现，c[1]的父节点为c[1+lowbit(1)]，为c[2]，而c[2]的父节点为c[2+2]，c[4]的父节点为c[8]，可以得出结论，c[i]父节点为c[i+lowbit(i)]，且整棵树的深度为log₂n + 1

（所以说这到底是哪个鬼才想出来的结构，当我搞明白的那一刻，我发现他是那么的巧妙神奇，这个结构是如此的优雅美丽。我搜了好半天都没搜到是谁发明的树状数组...）

接下来我们便可以学习上面提到的单点修改和前缀和查询操作了~

单点修改：

　　例如：add(3,5)，意味着c[3]的值要加上5，那么c[4]也要加上5，同理还有c[8]，那么我们只需要用循环，不断寻找x的父节点一一更新，直到x>n时结束即可，代码如下：

#define lowbit(x) (x & -x)
void add(int x, int d)
{
    for (; x <= n; x += lowbit(x)) c[x] += d;
}

查询前缀和：

　　例如：ask(7)，意味着输出c[7]+c[6]+c[4]的值，不难发现用x减去c[x]的区间长度就是我们要的下一个值，即c[x] + c[x-lowbit(x)]+...，代码如下：

int ask(int x)
{
    int sum = 0;
    for (; x > 0; x -= lowbit(x)) sum += c[x];
    return sum;
}

　　对于区间和，我们只需要分别求出前缀和相减即可。

对于以上两种操作复杂度均为O(logn)，n次询问为O(nlongn)。

 

 树状数组的扩展应用：差分数组(区间修改，单点查询)

首先我们引入差分数组b，用树状数组维护b的前缀和，即原数组a每个元素的增量

例如：a[5] = {1,2,6,5,3} 那么b[5] = {1,1,4,-1,-2}

现在我们进行区间修改，例如把区间[2,4]都加上2

则，a数组变为1,4,8,7,3，b数组变为1,3,4,-1,-4

不难发现，b数组只有b[2]和b[5]发生了变化，且b[2]+2而b[5]-2

故，我们得到这样的结论区间[l,r]+d时，我们只需要add(l,d),add(r+1,-d)，单点查询a[x]时，只需要ans=a[x]+ask(x)（原数+增量）。

 

区间修改，区间查询(待续...)