算法_八大排序算法总结

    最近笔试面试中经常考到排序算法，及其对应的时间复杂度和空间复杂度分析，现做如下总结。

一，冒泡排序

       思想：对于0~n-1，依次比较相邻两个数，前者比后者大就交换，一轮后A[n-1]是最大数，在对0~n-2执行以上步骤，则A[n-2]是第二大的数，循环执行上面的步骤即可，形象的可以理解为大的数一个个冒到后面去，所以叫冒泡排序。

     示意图：

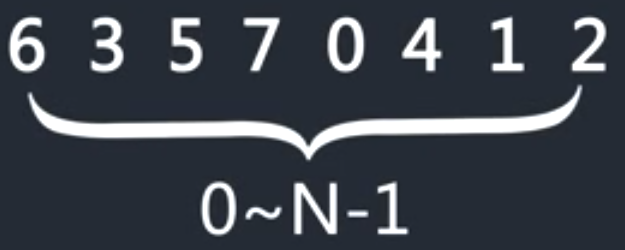
首先6和3比较，6比3大，交换

6和5比较，交换

6和7比较，不用交换

依次执行以上步骤，第一轮后，序列变为

接着，在0到n-2上执行以上步骤

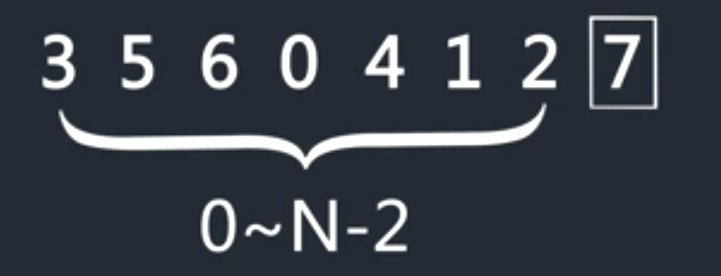
一轮过后，则变为

依次执行以上步骤，最后序列为

   时间复杂度：  O(n^2)

   空间复杂度：O(1)

   代码：

class BubbleSort {
public:
    int* bubbleSort(int* A, int n) 
    {
        int temp;
        // write code here
        for(int i = 0; i < n; i++)
        {
            for(int j = 0; j < n - i - 1; j++)
            {
                if(A[j] > A[j+1])
                {
                    temp = A[j];
                    A[j] = A[j + 1];
                    A[j + 1] = temp;
                }
            }
            
        }
        return A;
    }
};

 

 二，选择排序

     思想：在序列中依次选择最小值放到最前端，重复以上步骤，只到排序完成

    示意图：

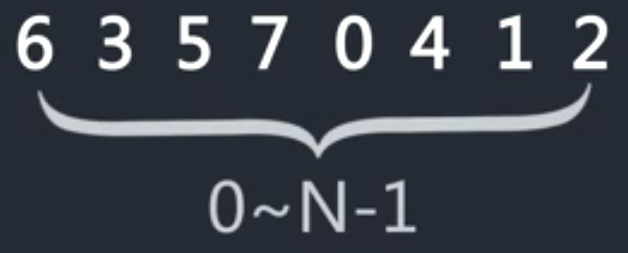
最小数为0，放到最前端

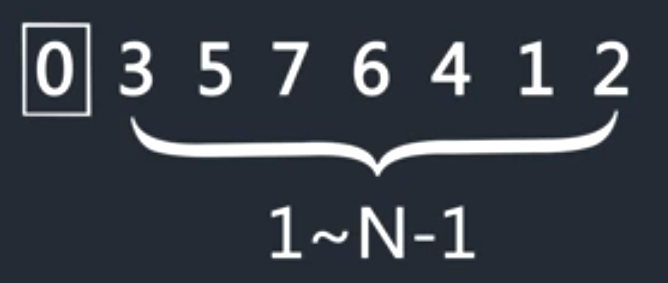
1到n-1最小数为1，放到最前端

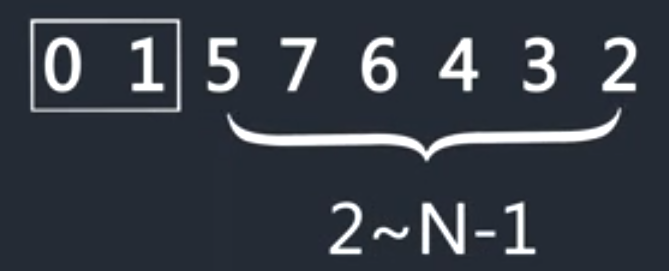
依次执行以上步骤，最后为

  时间复杂度：O(n^2)

   空间复杂度：O(1)

   代码：

class SelectionSort {
public:
    int* selectionSort(int* A, int n) 
    {
        // write code here
        //从前往后依次放入为排序的数组的最小值
        int min_b;
        int temp;
        for(int i = 0; i < n - 1; i++)
        {
            min_b = i;
            for(int j = i; j < n; j++)  //寻找最小值
            {
                if(A[min_b] > A[j])
                    min_b = j;
                    
            }
            temp = A[i];
            A[i] = A[min_b];
            A[min_b] = temp;
        }
        return A;
    }
};

 

 

三，插入排序

       思想：对于数组A[n]，保证前面的A[0]~A[m]是排序好的，再把A[m+1]插入到前面排好序的序列中，m递增，知道m=n-2

       示意图：

原始序列为：

6和5比较，6比5大，要交换

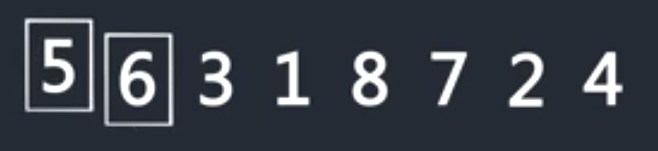
接下来把3插入到前面排好序的序列中，首先3和6比，6大，后移一位

接着3和5比较，5大，后移一位

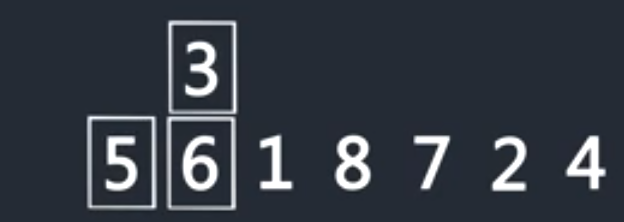
只到前面没有数了，或者前面的数比要插入的数小，就在对应的位置插入该数

再对1执行以上步骤

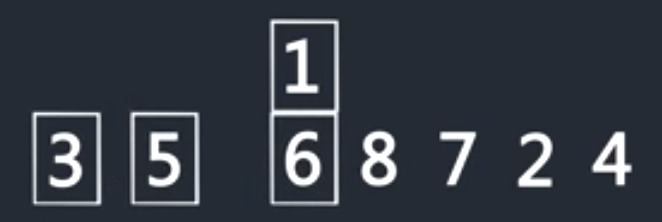
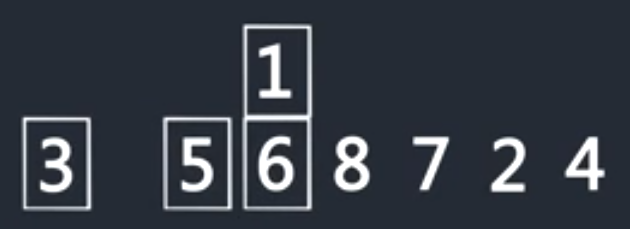
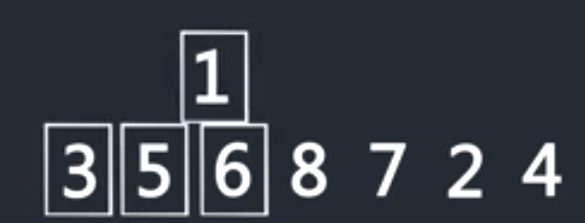
重复以上步骤，只到整个序列排序完成

   时间复杂度：O(n^2)

   空间复杂度：O(1)

       代码

class InsertionSort {
public:
    int* insertionSort(int* A, int n) 
    {
        // write code here
        int temp;
        for(int i = 1; i < n; i ++)
        {
            temp = A[i];
            for(int j = i - 1; j >= 0; j--)
            {
                if(temp < A[j])
                {
                    A[j + 1] = A[j];
                    if(j == 0)
                    {
                        A[j] = temp;
                    }
                }
                else
                {
                    A[j + 1] = temp;
                    break;
                }
            }
        }
        return A;
    }
};

 

 

四，归并排序

     思想：对数组中每个数看成是长度为1的有序区间，接着合并相邻两个长度为1的有序区间，变为长度为2的有序区间，接着合并相邻长度为2的有序区间变成长度为4的有序区间，依次进行，只到排序完成

    示意图：

    首先为长度为1的有序区间

  

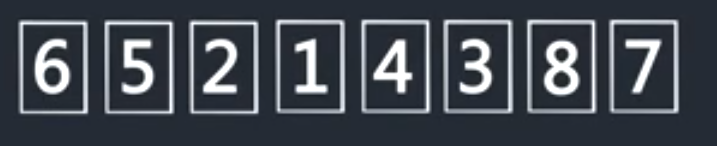
   合并为长度为2的有序区间

   合并为长度为4的有序区间

 

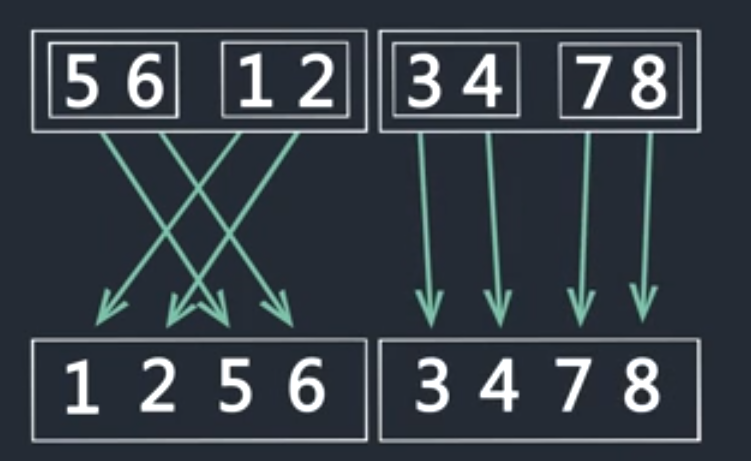
    合并为长度为8的有序区间，排序完成

     时间复杂度：O(nlogn)

     空间复杂度：O(N)

 

     代码

class MergeSort {
public:
    int* mergeSort(int* A, int n) 
    {
        mergeSort(A,0,n-1);
        return A;
        
    }
      void mergeSort(int* A, int left, int right)
    {
        if(left == right)
            return;
        int mid=(left+right)/2;
        mergeSort(A,left,mid);
        mergeSort(A,mid+1,right);
        merge_p(A,left,mid,right);
        return;
    }
    
    void merge_p(int* A, int left, int mid, int right)
    {
        int* temp = new int[right - left + 1];
        int l = left;
        int r = mid + 1;
        int k = 0;
        while(l <= mid && r <= right)
        {
            if(A[l] < A[r])
                temp[k++] = A[l++];
            else
                temp[k++] = A[r++]; 
        }
        while(l <= mid)
            temp[k++] = A[l++];
        while(r <= right)
           temp[k++] = A[r++]; 
        for(int i = 0; i < k; i++)
        {
            A[left + i] = temp[i];
        }
    }
    
};

 

   

五，快速排序

      思想：随机选择数组中的数，小于等于这个数的放在左边，大于这个数的放在右边，递归调用以上步骤，完成排序

      示意图：

     首先随机选择，划分区间

      

      递归调用，即可完成排序。

      

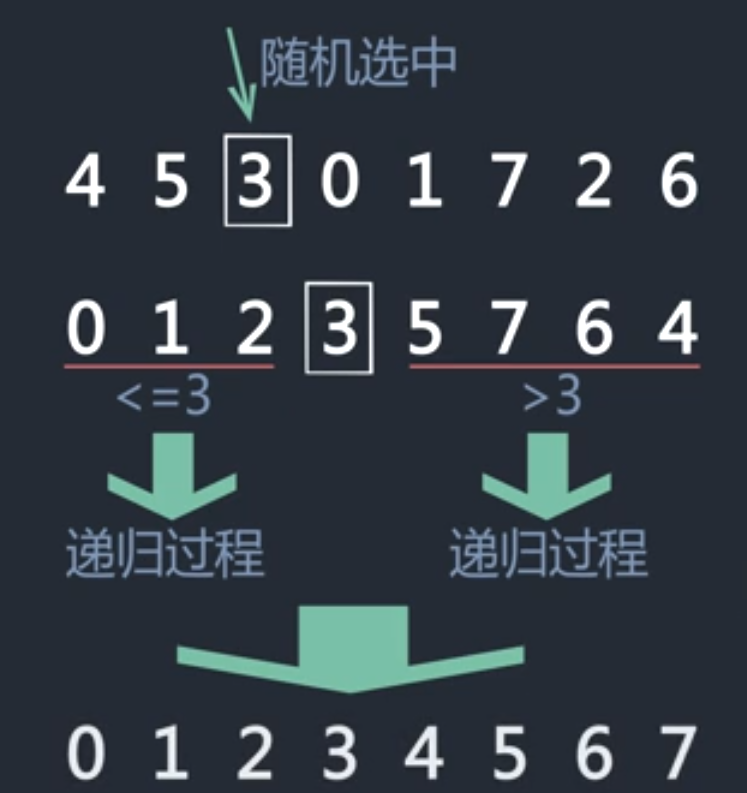
    问题的关键在于如何划分区间，即小于等于的数如何放在左边，大于的数如何放在右边，即Partition过程

    首先假设选择3为枢纽源

   

   把枢纽源和最后一个数字交换

    

   维持一个小于等于区间

    

   接下来从左到右遍历所有数，大于枢纽源的数则不动，小于等于枢纽源的数时把该数和小于等于区间的下一个数交换，并令小于等于区间右移一位，如此进行，只到最后一个数，即枢纽源，再把枢纽源和小于等于区间的下一个数交换即可。

   接上图，4，5,6都大于3不用动，0小于3，要与小于等于区间的下一个数即4交换位置，小于等于区间右移一位，即：

如此进行下去

 

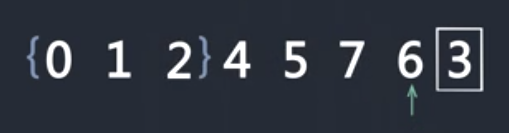
最后一步，把枢纽源3和小于等于区间的下一个数4交换位置

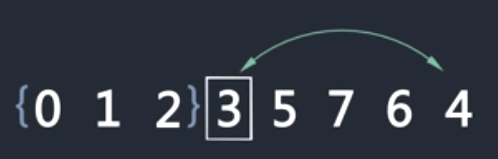
划分完毕，划分时间复杂度为O(n)。

  时间复杂度： O(nlogn)

  空间复杂度：O(logn) ~O(n)

代码

class QuickSort {
public:
     
    void swap(int &a, int &b)
    {
        int c;
        c = a;
        a = b;
        b = c;
    }
    
    void quick_s(int* A, int left, int right)   //枢纽元直接取中间值
    {
        if(left >= right )
            return;
        int mid = (left + right)/2;
        int key = left;
        swap(A[mid],A[right]);
        for(int i = left; i < right; i++)
        {
            if(A[i] < A[right])
            {
                swap(A[key],A[i]);
                key++;
            }
        }
        swap(A[key],A[right]);
        quick_s(A,left,key - 1);
        quick_s(A,key + 1,right);
    }
   
    
        
    int* quickSort(int* A, int n) 
    {
        // write code here
        quick_s( A, 0, n-1);
        return A;
    }
};

 

 

六，堆排序

   思想： 把数组构建为一个大小为n的大根堆，堆顶为所有元素的最大值，把堆顶元素和最后一个值交换，作为有序部分放在最后，接着调整剩下的n-1个元素的大根堆，第二大的值就是堆顶元素，在和该堆的最后一个元素交换，并脱离堆作为有序部分，重复以上步骤。

  示意图：

  原始数组为

构建最大堆

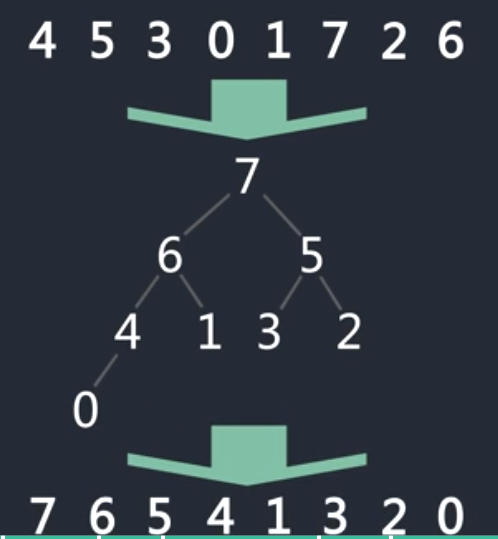
堆顶元素和最后一个数交换，作为有序部分放到最后

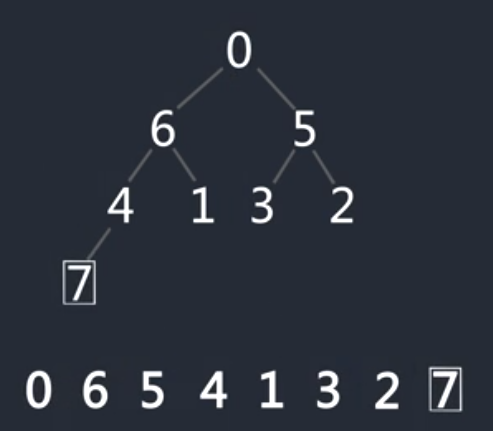
调整最大堆

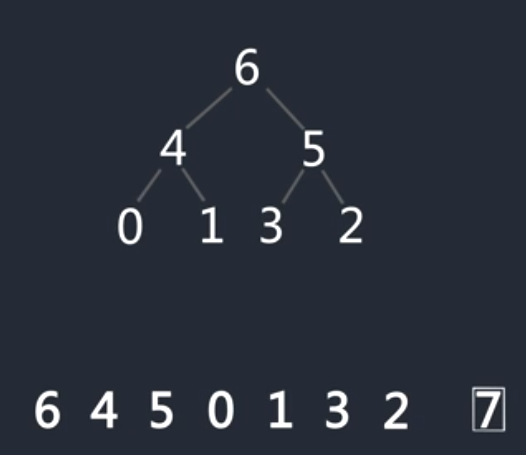
堆顶元素和最后一个数交换，作为有序部分放到最后

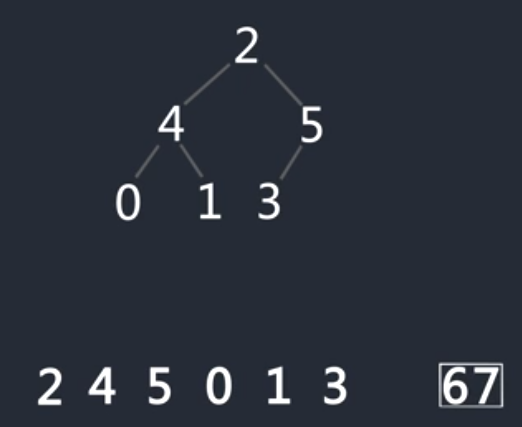
调整最大堆

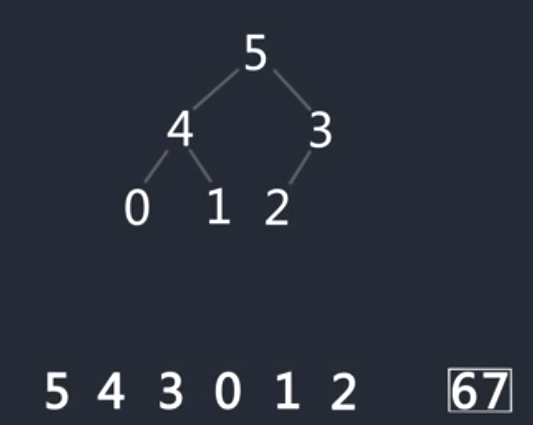
重复以上步骤，直到排序完成

   时间复杂度：O(nlogn)

   空间复杂度：O(1)

   代码

class HeapSort 
{
public:
    void Prcdown(int* A, int i, int n)
    {
        int tem;
        int Child;
        for(tem = A[i]; 2 * i + 1 < n; i = Child)
        {
             Child = 2 * i + 1;
              if(Child != n-1 && A[Child + 1] > A[Child])  //寻找较大的儿子
                  Child++;
              if(tem < A[Child])
                  A[i] = A[Child];
              else
                 break;
        }
        A[i] = tem;
        
    }
    void Swap(int &a, int &b)
    {
      int c;
      c = a;
      a = b;
      b = c;
    }
    int* heapSort(int* A, int n) 
    {
        // write code here
        int i;
       for(i = n / 2; i >= 0; i--)    //在数组上构建最大堆
          Prcdown(A,i,n);
        for(i = n - 1; i > 0; i--)
       {
          Swap(A[0],A[i]);   //开始排序，把最大值换到后面去
          Prcdown(A,0,i);   //整理堆，剩下元素的最大值会回到开头
       }
        return A;
    }
};

 

 

七，希尔排序

     思想：希尔排序是插入排序的改良版，插入排序的步长为1，希尔排序的步长依次递减。

    示意图：

   假设原始数组为以下，步长为3

    

   前三个数不考虑

  

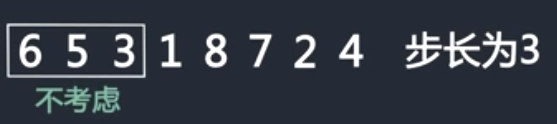
  从1开始比较，步长为3跳3步和6比较，6比1大，交换位置

1再往前跳3步就越界，因此开始比较8，跳3步和5比较，8比5大，不交换位置

停止8的交换，开始下一个数7 的交换，7比3大，不用交换

停止7的交换，开始2的交换，2和6比，2比6小，交换位置

2再跳3步和1比较，2比1大，不用交换，停止2的比较，开始4的交换，4和8比，4比8小，交换位置

4再跳3步和5比较，4比5小，交换位置

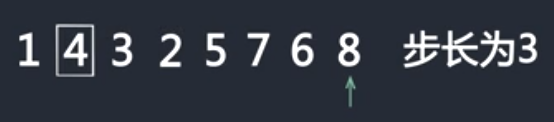
4再跳3步，越界，停止比较，步长为3调整结束，接下来步长为2和1调整，得到结果

    时间复杂度：O(nlogn)

   空间复杂度：O(1)

  代码

class ShellSort 
{
public:
    int* shellSort(int* A, int n) 
    {
        // write code here
        int i, j;
        int Increment = n/2;
        int tmp;
        while(Increment >= 1)
        {
            for(i = Increment; i < n; ++i)
            {
                tmp = A[i];
                for(j = i - Increment; j >= 0 && tmp < A[j]; j = j - Increment)
                {
                    A[j + Increment] = A[j];
                }
                A[j + Increment] = tmp;
            }
            Increment = Increment / 2;
        }
        return A;
    }
};

 八，通排序

     桶排序不是基于比较的排序，因此时间复杂度可以达到O(n)，空间复杂度为O(M)，M为桶的个数，桶排序的思想在于是先把元素放入对应的桶中，再到出，结果即为排完序的结果。

     基于桶排序思想的排序算法有基数排序和计数排序，原理差不多。

    具体请看我的另外一篇博客https://www.cnblogs.com/1242118789lr/p/6858486.html

 

   总结：

   稳定的算法：冒泡排序，插入排序，归并排序，桶排序

   不稳定的算法：选择排序，快速排序，希尔排序，堆排序

   元素的移动次数与关键字的初始排列次序无关的是：基数排序

   元素的比较次数与初始序列无关的是：选择排序

 

   夜深了，，，

 

   天亮了，昨晚平安夜。