算法导论_动态规划_最长回文子序列

一、问题的描述

回文序列(Palindromic sequence, Palindrome)是指正向遍历和反向遍历完全相同的序列，例如字符串“AAAAA”显然是一个回文序列，又如字符串“ABC@CBA”也是一个回文序列。现在，我们要在一个（字符）序列中找出最长回文子序列的长度。例如字符序列"BBABCBCAB"，最长回文子序列是“BACBCAB”（可能不唯一），它的长度是7；子序列"BBBBB"和"BBABB"虽然也是回文序列，但却不是最长的，因此不合题意。

二、分析

对任意字符串，如果头和尾相同，那么它的最长回文子序列一定是去头去尾之后的部分的最长回文子序列加上头和尾。如果头和尾不同，那么它的最长回文子序列是去头的部分的最长回文子序列和去尾的部分的最长回文子序列的较长的那一个。

 

设字符串为s，f(i,j)表示s[i..j]的最长回文子序列。 

则有

当i>j时，f(i,j)=0。 

当i=j时，f(i,j)=1。 

当i<j并且s[i]=s[j]时，f(i,j)=f(i+1,j-1)+2。 

当i<j并且s[i]≠s[j]时，f(i,j)=max( f(i,j-1), f(i+1,j) )。 

由于f(i,j)依赖i+1，所以循环计算的时候，第一维必须倒过来计算，从s.length()-1到0。 

最后，s的最长回文子序列长度为f(0, s.length()-1)。

 

有如下公式：

 

 

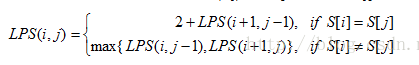
代码如下：

 

#include<iostream>
#include<cmath>
#include<algorithm>
using namespace std;

#define MAX 100

int f[MAX][MAX] = { 0 };
int b[MAX][MAX] = { 0 };
int flag = 0;


void Lps_length(string &str)
{
	int len = str.length();

	for (int i = len - 1; i >= 0; --i)
	{
		f[i][i] = 1;
		for (int j = i+1; j < len; ++j)
		{
			if (str[i] == str[j])
			{
				f[i][j] = f[i + 1][j - 1] + 2;
				b[i][j] = 0;
			}   
			
			else if (f[i + 1][j] >= f[i][j - 1])
			{
				f[i][j] = f[i + 1][j];
				if(f[i + 1][j] == f[i][j - 1])
					b[i][j] = 2;
				else
				   b[i][j] = -1;
			}
				
			else
			{
                f[i][j] = f[i][j - 1];
			    b[i][j] = 1;
			}
			
		
		}
	}
	
}

void printf_Lps(int b[MAX][MAX],int i,int j,const string &str)
{
	if (i < 0 || j < 0)
	{
		return;
	}
	
	if (b[i][j] == 0)
	{
		if (j >= 0 && j <= str.length() - 1)
		{
		cout << str[j];
		}
		
		if (i == j)
		{
			flag = 1;
		}

		if(flag == 0)
		    printf_Lps(b, i + 1, j - 1,str);
		else
			printf_Lps(b, i - 1, j + 1, str);
		
		
	}

	else if (b[i][j] == 2 || b[i][j] == 1)
	{
		if (flag == 0)
		    printf_Lps(b, i, j - 1,str);
		else
			printf_Lps(b, i, j + 1, str);
	}

	else if(b[i][j] == -1)
	{
		if (flag == 0)
		    printf_Lps(b, i + 1, j,str);
		else
			printf_Lps(b, i - 1, j, str);
	}
}


int main()
{

	string str = "GTJYTTHA";


	Lps_length(str);

	for (int i = 0; i <= str.length ()-1; ++i)
	{
		for (int j = 0; j <= str.length() - 1; ++j)
		{
			cout << b[i][j] << "\t";
		}
		cout << endl;
	}

	cout << f[0][str.length() - 1] << endl;

	printf_Lps(b, 0, str.length() - 1,str);

	cout << endl;
	return 0;
}

　　上述代码在计算最长回文子序列的长度时计算都是正确的，但是在打印最长回文子序列时有时出现问题，比如在输入character时，输出的是 cara ，而不是carac，调试了很久，也找不出问题，伤心，哪位网友要是看出来问题在哪请留言问题在哪，万分感谢

 

  调试bug是一个痛苦的过程

 

夜深了，