大数分析（6）——Y序列

前言

然后是Y序列，0-Y可以直接与BMS相互转换，而基本的1-Y序列（常说的Y序列就是这个）便有着极大的提升，甚至可以提升到n-Y，\(\omega-\)Y
BMS和Y序列，便如同强者界的天道、奥加一般（
同样的，后面由于缺少标定记号可能会跳过大段/直接开鸽

阶差为1的情况

请参考PrSS，完全一致，极限同样是\(\epsilon_0\)

阶差大于1的情况

我们需要引入差分序列，逐次差分使得阶差为1
基础版——0-Y的情况
0-Y与BMS互转
然后我们来看看真正的Y序列（1-Y）
在\(Y(1,2,...)\)的时候，通过逐次差分总能使各列最上面全部变成1，所以直接复制山脉图然后从上往下填表
一个简单的\(Y(1,2,4,8,16,32)\)

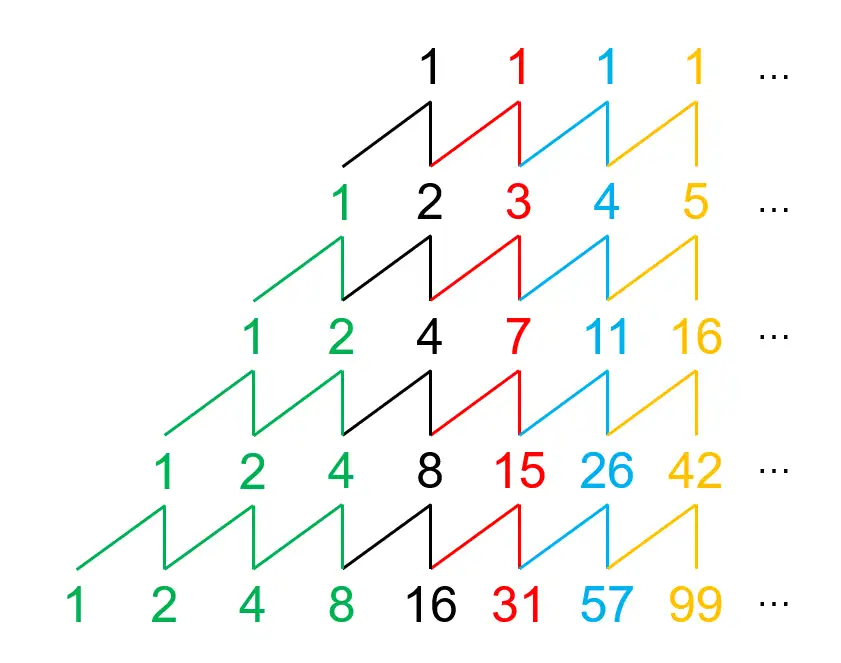
复杂一点的\(Y(1,2,4,8,10,8)\)的展开

---

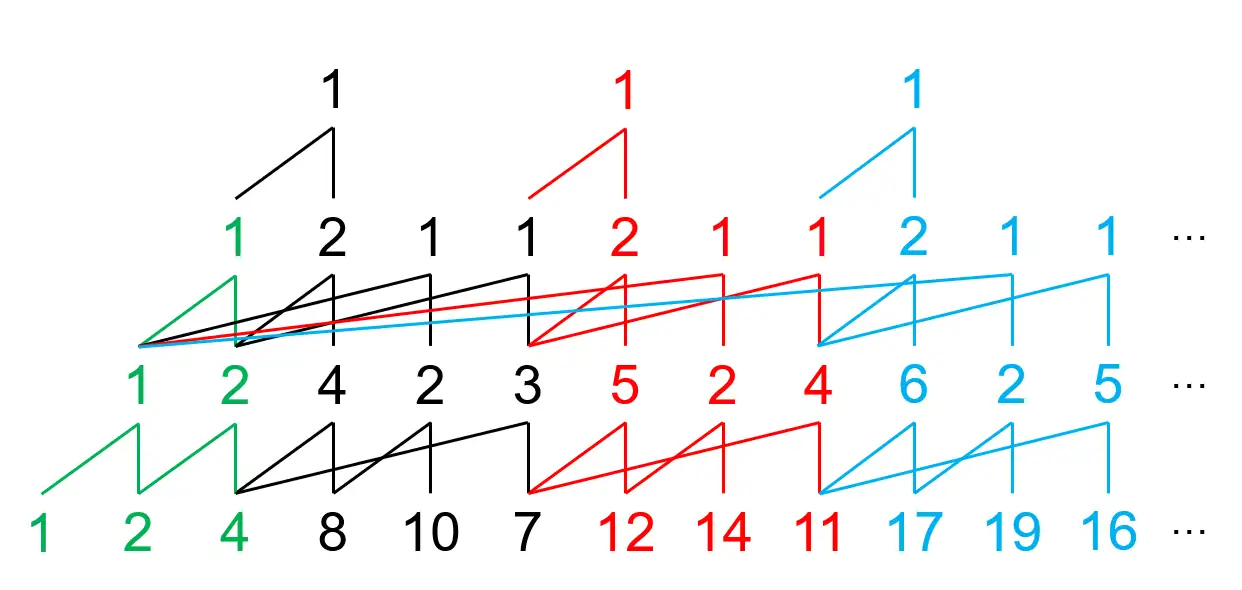
然后我们试着展开\(Y(1,3)\)，上面那层是2，这好吗？这不好
我们把每一列最上面的那一个全部提出来再排成一列，保持原来的父项关系，然后再画山脉图，复制
话是这么说，但是还是有很多细节的
1-Y的展开规则
一位霓虹佬的网站，可以对答案

枚举

\[1,2=1,1,...=\omega\\ 1,2,1=\omega+1\\ 1,2,1,2=\omega2\\ 1,2,2=1,2,1,2,...=\omega^2\\ 1,2,2,2=\omega^3\\ 1,2,3=1,2,2,2,...=\omega^\omega\\ \]

然后阶差开始升到2

\[1,2,4=1,2,3,4,5,...=\epsilon_0\\ 1,2,4,1,2,4=\epsilon_02\\ 1,2,4,2=1,2,4,1,2,4,...=\omega^{\epsilon_0+1}\\ 1,2,4,2,4=1,2,4,2,3,4,5,...=\omega^{\epsilon_02}\\ 1,2,4,3=1,2,4,2,4,...=\epsilon_0^{\epsilon_0}\\ 1,2,4,4=1,2,4,3,5,4,6,5,7,6,...=\epsilon_1 \]

Y序列开始展现出不规律性了，之后不再展开

\[1,2,4,4,1,2,4,4=\epsilon_12\\ 1,2,4,4,4=\epsilon_2\\ 1,2,4,5=\epsilon_\omega\\ 1,2,4,5,4=\epsilon_{\omega+1}\\ 1,2,4,5,4,4=\epsilon_{\omega+2}\\ 1,2,4,5,4,5=\epsilon_{\omega2}\\ 1,2,4,5,5=\epsilon_{\omega^2}\\ 1,2,4,5,6=\epsilon_{\omega^\omega}\\ 1,2,4,5,7=\epsilon_{\epsilon_0}\\ 1,2,4,5,7,7=\epsilon_{\epsilon_1}\\ 1,2,4,5,7,8=\epsilon_{\epsilon_\omega}\\ 1,2,4,5,7,10=\epsilon_{\epsilon_{\epsilon_0}} \]

为什么最后那个的最后一项是10？把山脉图画出来大概就理解了

\[1,2,4,6=\zeta_0\\ 1,2,4,6,4=\epsilon_{\zeta_0+1}\\ 1,2,4,6,4,5=\epsilon_{\zeta_0+\omega}\\ 1,2,4,6,4,5,7=\epsilon_{\zeta_0+\epsilon_0}\\ 1,2,4,6,4,5,7,9=\epsilon_{\zeta_02}\\ 1,2,4,6,4,6=\zeta_1\\ 1,2,4,6,5=\zeta_\omega\\ 1,2,4,6,5,7,9=\zeta_{\zeta_0}\\ 1,2,4,6,6=\eta_0\\ 1,2,4,6,6,4,6,6=\eta_1\\ 1,2,4,6,6,5,7,9,9=\eta_{\eta_0}\\ \]

看上去一些重复结构的特征已经确定了

\[1,2,4,6,6,6=\varphi(4,0)\\ 1,2,4,6,6,6,5=\varphi(4,\omega)\\ 1,2,4,6,7=\varphi(\omega,0)\\ 1,2,4,6,7,4,6,7=\varphi(\omega,1)\\ 1,2,4,6,7,5=\varphi(\omega,\omega)\\ 1,2,4,6,7,6=\varphi(\omega+1,0)\\ 1,2,4,6,7,6,4,6,7=\varphi(\omega,\varphi(\omega+1,0)+1)\\ 1,2,4,6,7,7=\varphi(\omega^2,0)\\ 1,2,4,6,7,8=\varphi(\omega^\omega,0)\\ 1,2,4,6,7,9=\varphi(\epsilon_0,0)\\ 1,2,4,6,7,9,9=\varphi(epsilon_1,0)\\ 1,2,4,6,7,9,11=\varphi(\zeta_0,0)\\ 1,2,4,6,7,9,11,11=\varphi(\eta_0,0)\\ 1,2,4,6,7,9,11,12=\varphi(\varphi(\omega,0),0)\\ 1,2,4,6,7,9,11,12,14=\varphi(\varphi(\epsilon_0,0),0)\\ \]

可以看到Y序列的层级复杂之后会越来越长，而且分析时稍有不慎就会跳掉从而出锅

\[1,2,4,6,8=\Gamma_0\\ 1,2,4,6,8,4=\epsilon_{\Gamma_0+1}\\ 1,2,4,6,8,4,6=\zeta_{\Gamma_0+1}\\ 1,2,4,6,8,4,6,8=\Gamma_1 \]

上面两行之间其实跳掉了一堆节点，不过大致一样就略过了

\[1,2,4,6,8,5=\Gamma_\omega\\ 1,2,4,6,8,5,7,9,11=\Gamma_{\Gamma_0}\\ 1,2,4,6,8,6=\varphi(1,1,0)\\ 1,2,4,6,8,6,7,9,11,13=\varphi(1,\Gamma_0,0)\\ 1,2,4,6,8,6,8=\varphi(2,0,0)\\ 1,2,4,6,8,7=\varphi(\omega,0,0)\\ 1,2,4,6,8,7,9,11,13=\varphi(\Gamma_0,0,0)\\ 1,2,4,6,8,8=\varphi(1,0,0,0)\\ 1,2,4,6,8,9=\varphi(1@\omega)=\psi(\Omega^{\Omega^\omega})\\ 1,2,4,6,8,10=\psi(\Omega^{\Omega^\Omega})\\ \]

和BMS同样飞速完成了\(\varphi\)段的跨越

\[1,2,4,6,8,10,4=\psi(\Omega^{\Omega^\Omega}+1)\\ 1,2,4,6,8,10,6=\psi(\Omega^{\Omega^\Omega+1})\\ 1,2,4,6,8,10,8=\psi(\Omega^{\Omega^{\Omega+1}})\\ 1,2,4,6,8,10,10=\psi(\Omega^{\Omega^{\Omega2}})\\ 1,2,4,7=\psi(\Omega_2) \]

阶差到3了，到达\(\Omega\)指数塔了

\[1,2,4,7,11=\psi(\Omega_3)\\ 1,2,4,8=\psi(\Omega_\omega) \]

已经等同两行BMS了

\[1,2,4,8,10=\psi(\Omega_{\omega}\Omega)\\ 1,2,4,8,11=\psi(\Omega_\omega\Omega_2)\\ 1,2,4,8,11,8=\psi(\Omega_{\omega}^2)\\ 1,2,4,8,11,12=\psi(\Omega_{\omega}^\omega)\\ 1,2,4,8,11,13=\psi(\Omega_{\omega}^\Omega)\\ 1,2,4,8,11,15=\psi(\Omega_{\omega+1})\\ 1,2,4,8,12=\psi(\Omega_{\omega^2})\\ 1,2,4,8,12,11,8,12=\psi(\Omega_{\omega^2}^2)\\ 1,2,4,8,12,11,14,8,12=\psi(\Omega_{\omega^2}^{\Omega_{\omega^2}})\\ 1,2,4,8,12,11,15=\psi(\Omega_{\omega^2+1})\\ 1,2,4,8,12,13,15=\psi(\Omega_{\epsilon_0})\\ 1,2,4,8,12,14=\psi(\Omega_{\Omega})\\ 1,2,4,8,12,14,17=\psi(\Omega_{\psi(\Omega_2)})\\ 1,2,4,8,12,15=\psi(\Omega_{\Omega_2})\\ 1,2,4,8,12,15,9=\psi(\Omega_{\Omega_{...}}) \]

之后就需要用反射的OCF标定了，但是我还没看到一个看的顺眼的，所以直接略过

\[1,2,4,8,16=(0,0,0,0)(1,1,1,1)\\ 1,3=(0)(1^\omega)\\ 1,3,4,2,5,8=(0)(1^{\omega^2}) \]

从上到下分别是4行，\(\omega\)行和\(\omega^2\)行（目前有理论的TBMS）
Y序列薄纱BMS（
其极限为$$SYO=1,\omega$$
你说为什么是\(Small~Yukito~Ordinal\)？
因为还可以把\(1-Y\)加强到\(\omega-Y\)乃至画饼的\(\Omega-Y\)