计算机图形学入门笔记（三）（L10-L12）

课程传送门

L10 Geometry1(Introduction)

Bump Mapping 凹凸贴图
我们可以通过修改每一点“高度”，进而改变该点的法向量来改变该点的性质
以二维下情况为例，三维类推
在自然坐标系下（也就是以在某曲线上的这个点为原点建系），设法向量为\(\pmb{n}=(0,1)\)

原来的切向量是\((1,0)\)，你的纵坐标增加了\(d\pmb{p}\)
所以你的切线方向变成了\((1,d\pmb{p})\)，其中\(d\pmb{p}=c*\Delta h\)，\(c\)为一个衡量凹凸贴图影响程度的常数
所以法向量就是\((-d\pmb{p},1)\)，单位化一下即可
三维类推

\[n=(-\frac{d\pmb{p}}{d\pmb{u}},-\frac{d\pmb{p}}{d\pmb{v}},1) \]

其中前两项是\(p\)对\(u,v\)两个方向的差分（导数）

Displacement Mapping 位移贴图
直接移动顶点
要求三角形足够细
实现可以看作业3

---

Implict Surface（显式坐标）
优：很容易判断在内/外
劣：计算坐标比较难
Explicit Surface（隐式坐标）
优劣和上面相反

---

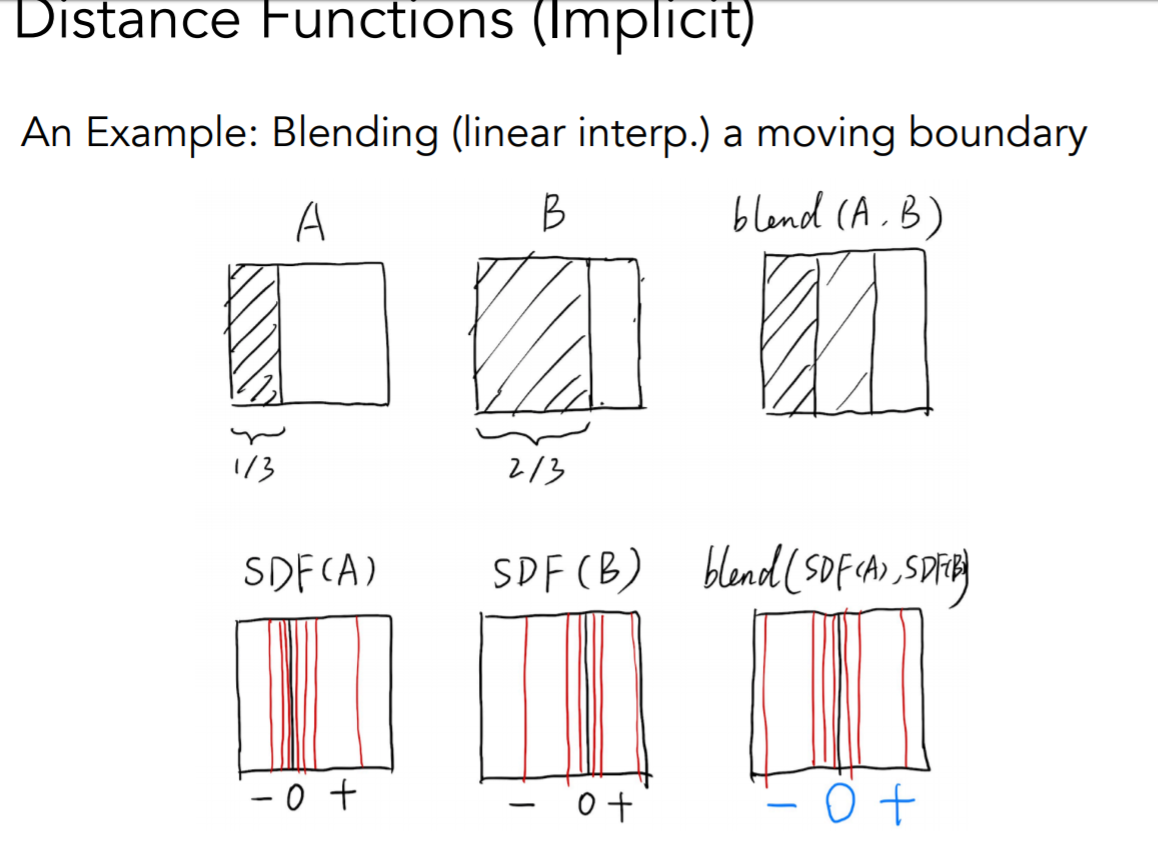
Distance Function(SDF)
这个我没看的很懂……
总而言之直接放图吧

L11 Geometry2(Curves and Surfaces)

曲线与曲面的表示方法：

1. 点集 这个没什么好讲的
2. Polygon Mesh（多面体网格？）广泛应用

---

贝塞尔曲线的解法（De Casteljau’s algorithm）
以三个点的情况为例

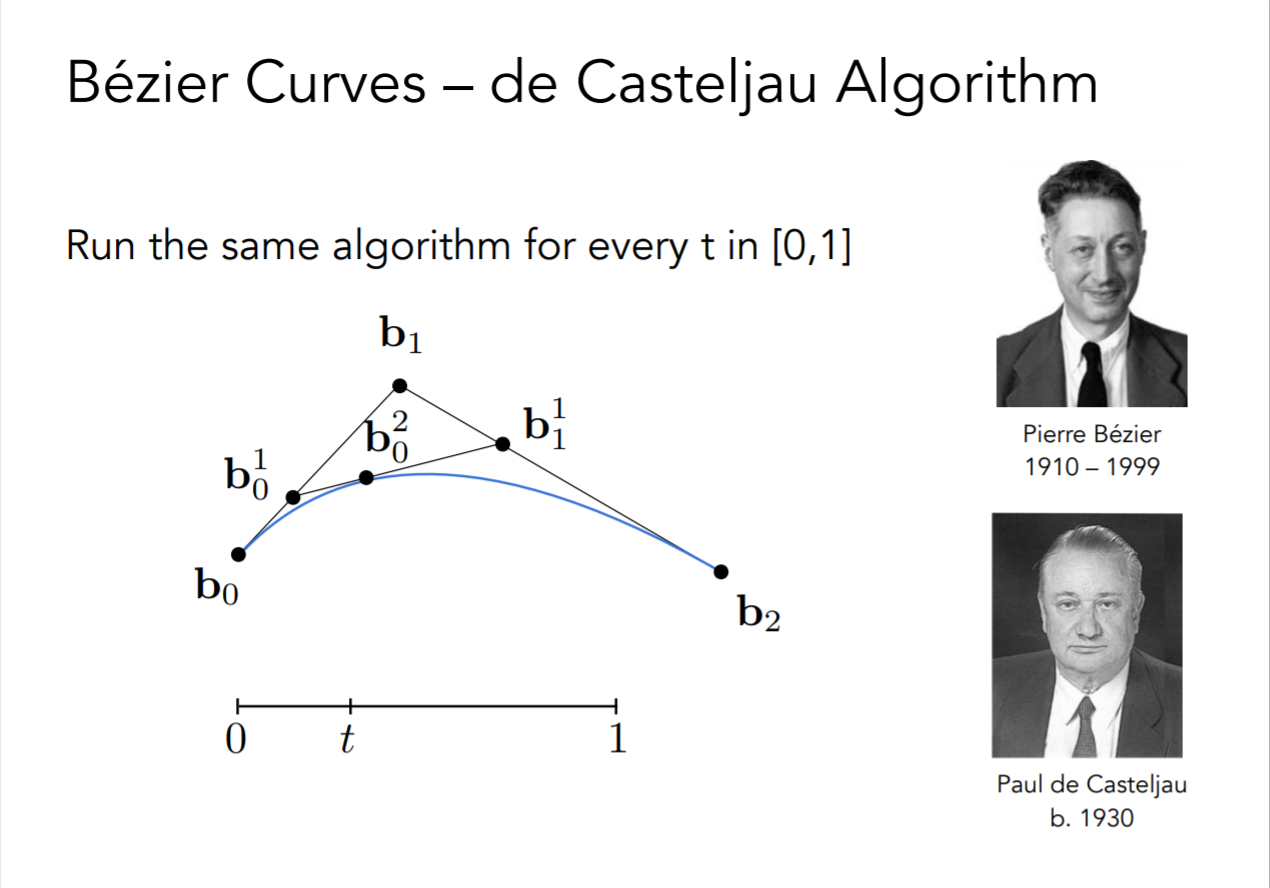
就是先在两条边上取\(t\)分点，再把这两个点连起来，再取\(t\)分点
最后把坐标看成以\(t\)为参数的参数方程即可
多点类似的递归即可
也可以直接套公式

\[\pmb{b}^n(t)=\sum_{j=0}^{n}{\pmb{b}_{j}}B^n_{j}(t)\\ B^n_{i}(t)=\binom{n}{i}t^i(1-t)^{n-i}\]

其中\(\pmb{b}_j\)是各点坐标，\(B^n_{i}{t}\)其实可以看成\([t+(1-t)]^n\)的二项式展开

然而这个东西稍微把一个点坐标变一下就要重新算一遍，而且点一多就很麻烦
所以一般会采用分段贝塞尔的方法

---

贝塞尔曲面
比方说你有4*4个点
你对每一行的点求一个贝塞尔曲线，求出来四条线
对于每一个\(t\)，再对这四条线上对应的四个点求一个贝塞尔曲线，参数为\(v\)
线动成面
所以我们可以用两个参数\(u,v\)来描述这个曲面

L12 Geometry3

Mesh Subdivision（网格划分）

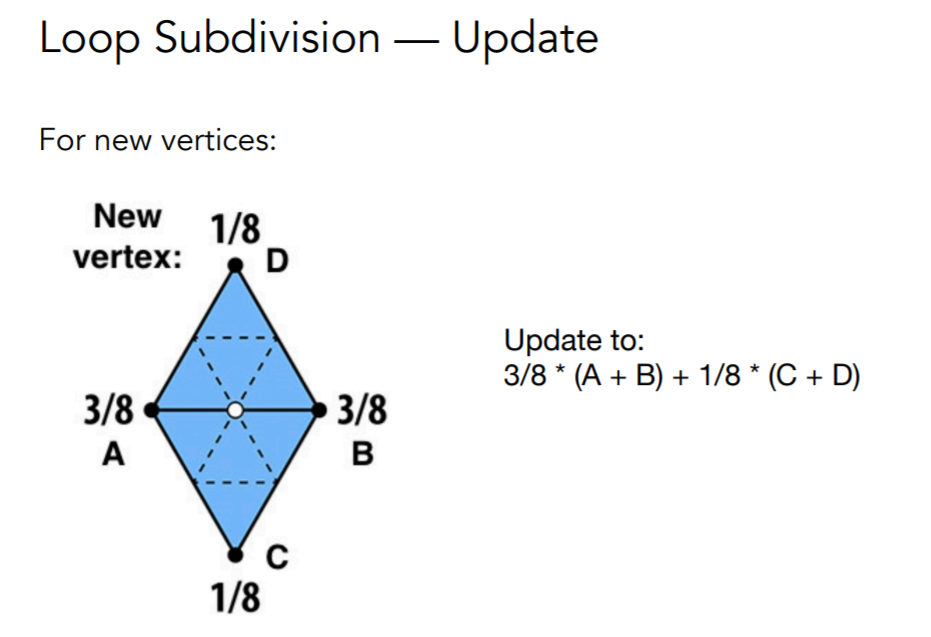
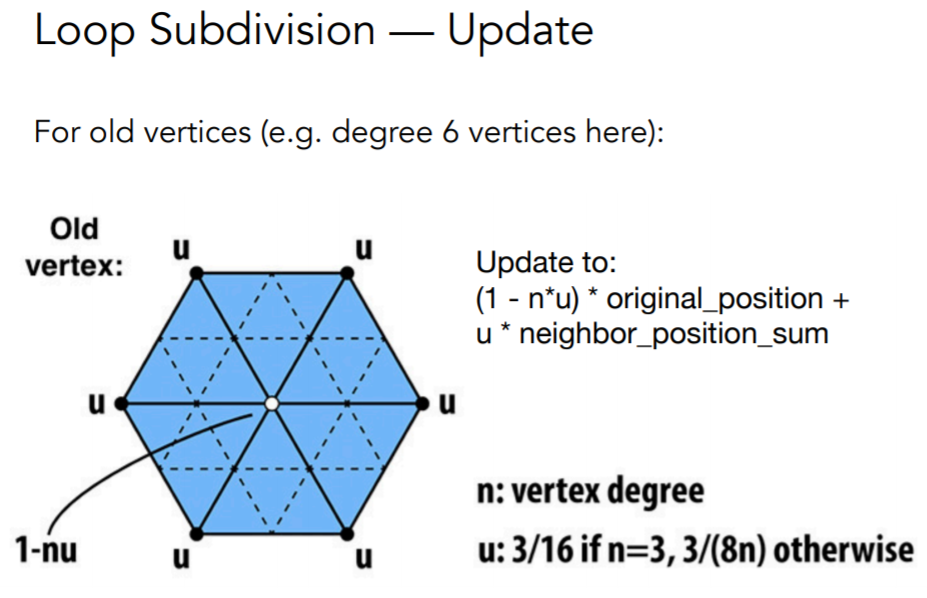
1. Loop Subdivision
   只能处理三角形网格
   将一个三角形分成四个小三角形，新老点分别处理位移
   
   
2. Catmull-Clark
   将每一个三角形分成四个四边形，分为面心，边心和老点分别处理
   

---

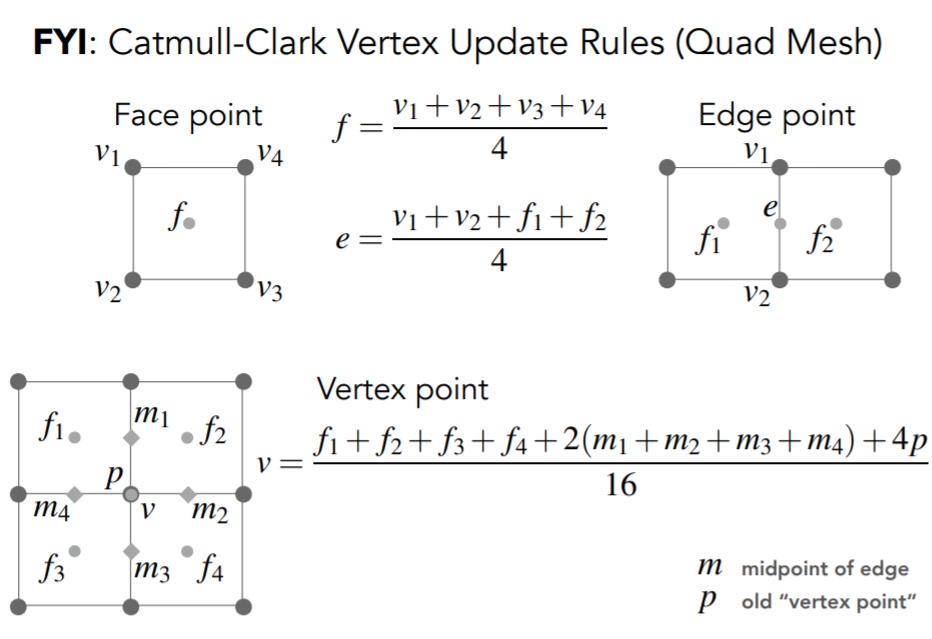
Mesh Simplification（网格简化）
就是类似于最小二乘法的一个算法
再加上贪心地每次删掉一条边（虽然我并不知道怎么实现）

---

Shadow Mapping
一个地方可见（不是阴影）必然要同时能被看到和被光线照到
所以做两遍\(Z-Buffer\)，第一遍把光源看作相机，得到一张深度图
第二遍首先要看这个点是否能被看到，其次要看能否被光线看到
判别方法是该点与光源的距离与该点在深度图上与光源的距离是否大致相等