计算机图形学入门笔记（二）（L5-L9）

课程传送门

L5 Rasterization(Triangles)光栅化

直接上图吧


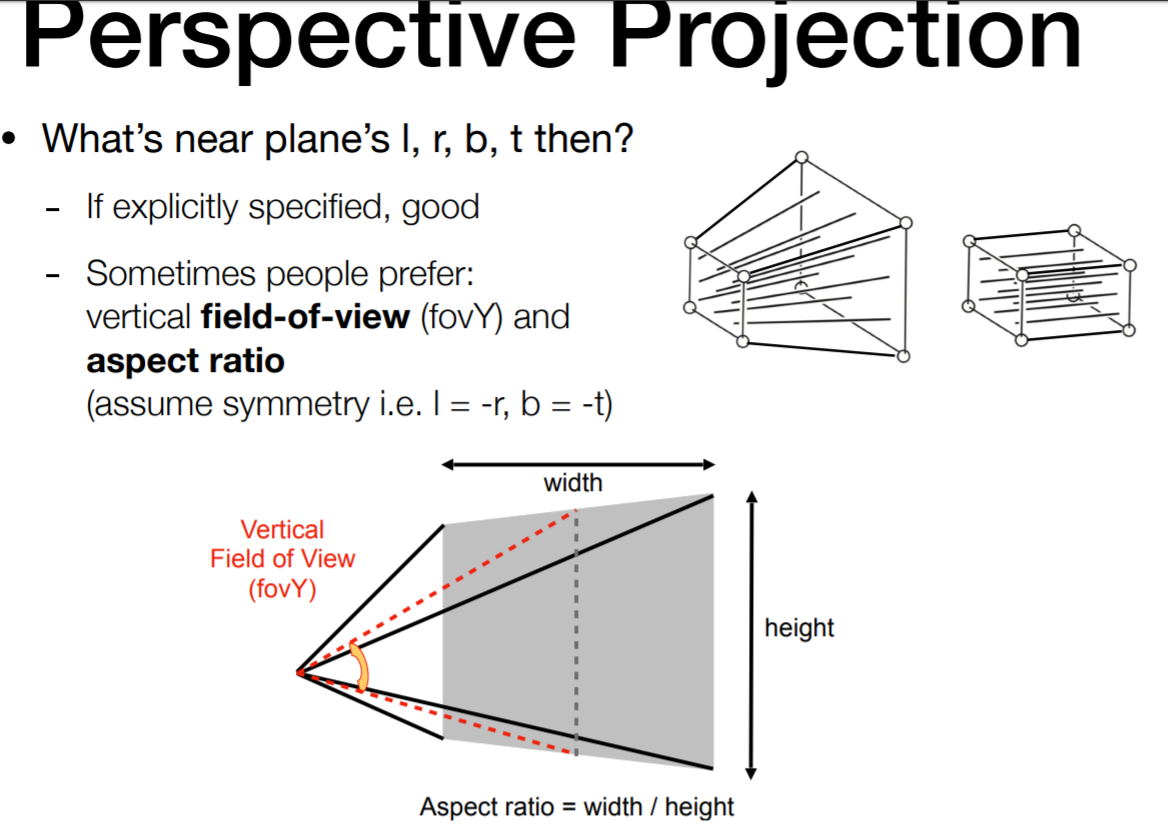
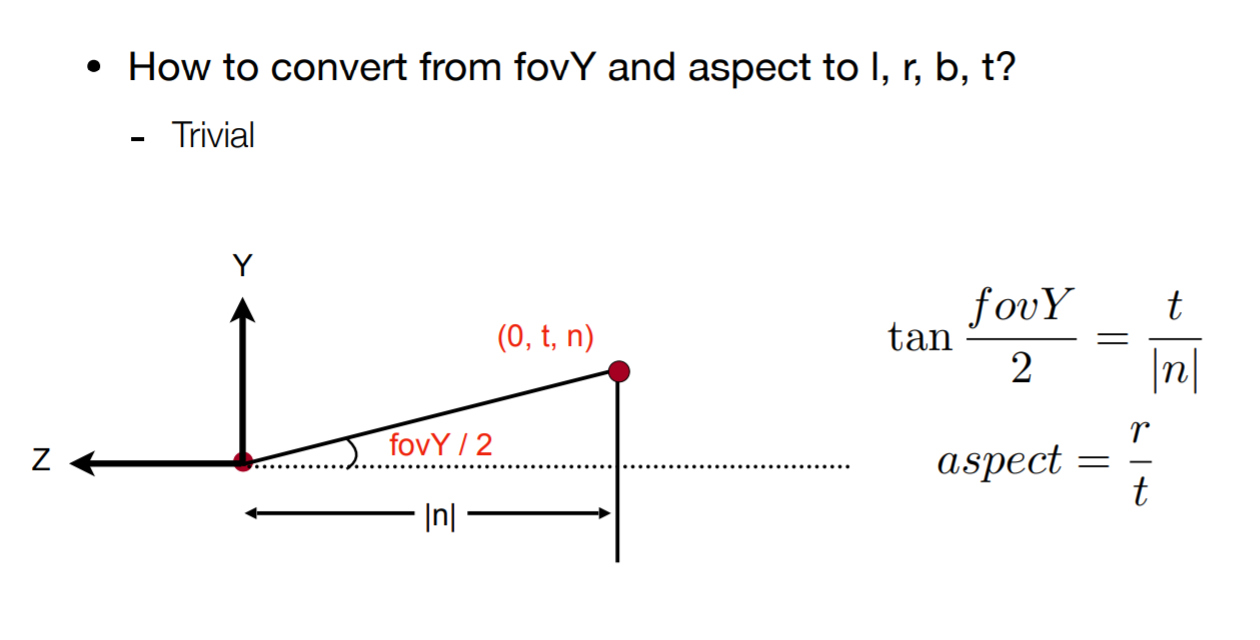
其中fov为视角，aspect ratio为宽高比。
所以有

\[top=|n|\tan\frac{fov}{2}\\ right=top*ratio\]

其中top是指y轴坐标最大为多少，right是指x轴坐标最大为多少
换句话讲，这三个参数可以定义一个平面\([-right,right]\times[-top,top]\times n\)

---

变换流程

先移物体，再移相机，再投影，最后视口。

---

视口变换：将投影后的坐标变换为屏幕坐标
Cube->Screen(\([-1,1]^2\to[0,w]\times[0,h]\))

\[M=\begin{bmatrix} \frac{w}{2}&0&0&\frac{w}{2}\\ 0&\frac{h}{2}&0&\frac{h}{2}\\ 0&0&1&0\\ 0&0&0&1 \end{bmatrix} \]

---

判断一个点是不是在给定三角形内部：
直接三个叉积
给定点逆时针方向依次叉积，全部为正则在内部。
顺时针方向全部为负，则在内部。

---

bounding box
直接上图吧

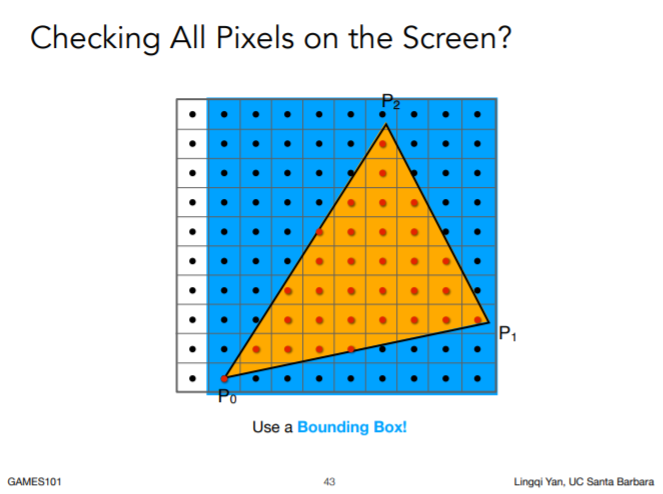
L6 Rasterization(Antialiasing)抗锯齿

一节划水的课？
时域和频域的转化听的不是很懂，不过并没有什么影响？
高频的相当于边界，低频相当于渐变。
先模糊再处理相当于把高频抹掉，防止出现重复。

MSAA算法就是直接爆算每个像素，划分成几个小像素
脑子：我听懂了，代码：你说什么？

L7 Shading1

Z-Buffer算法
假定z坐标全部是正的
所以小的近，大的远
所以对于每一个像素去算每一个深度，更新为深度最小的即可

---

Blinn-Phong算法
这是一个经验模型，所以简化了/近似了很多东西；并且这是一个局部光模型，所以环境光可以直接简化
光线分解为：镜面反射（高光），漫反射，环境光
光线方向\(\pmb{l}\)，平面法向量\(\pmb{n}\)，视角\(\pmb{v}\)，三个向量都是单位向量

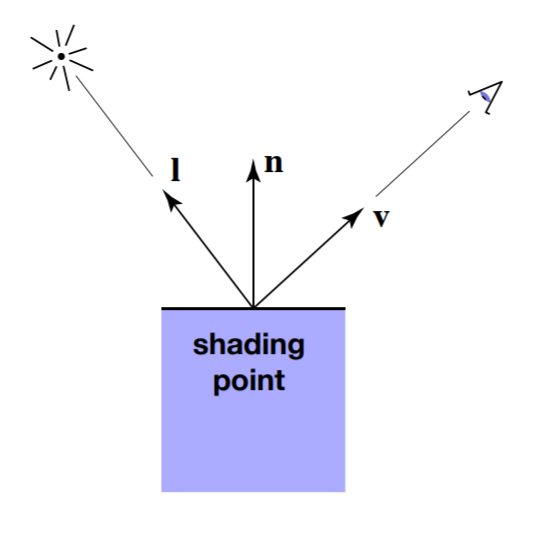
1. 漫反射

\[cos\theta=\pmb{l}*\pmb{n} \\ L_d=k_d\frac{I}{r^2}\max(0,\pmb{n}*\pmb{l})\]

\(L_d\)为漫反射强度，\(k_d\)为一个与平面有关的参数，最后取max是因为如果是钝角就相当于没有光照。
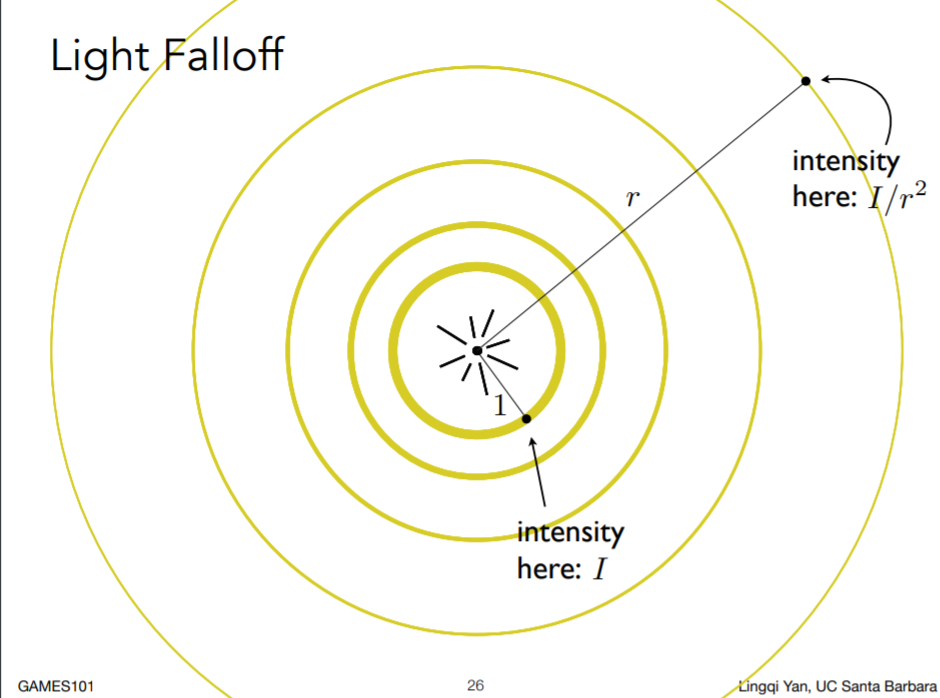
\(\frac{I}{r^2}\)可以看下图，其中\(I\)是点光源的强度
各个圈是一开始发出的一圈光
由于这是一圈光，所以能量守恒
所以最里面一圈和最外面一圈的能量相同

2. 镜面反射（高光）
由于观察方向和镜面反射方向接近，因而产生

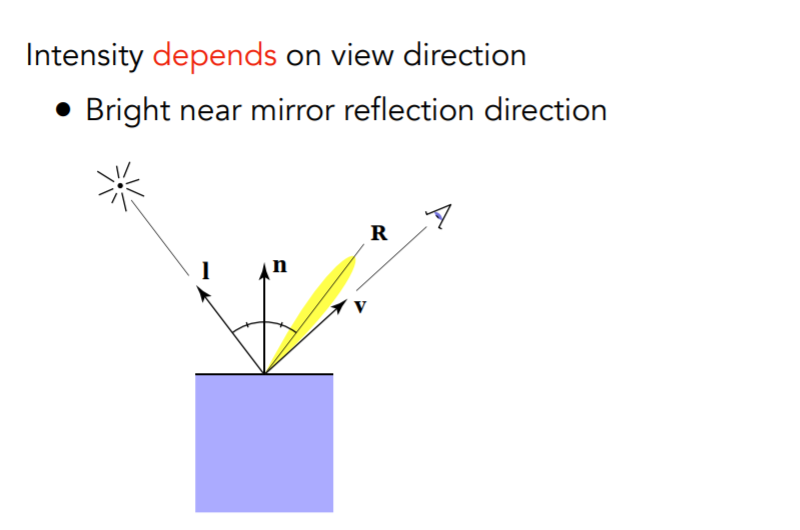
所以我们要求的夹角应该是\(\pmb{R}*\pmb{v}\)
然而由于\(R\)是一个反射之后得到的向量，所以计算量会很大
于是近似一下

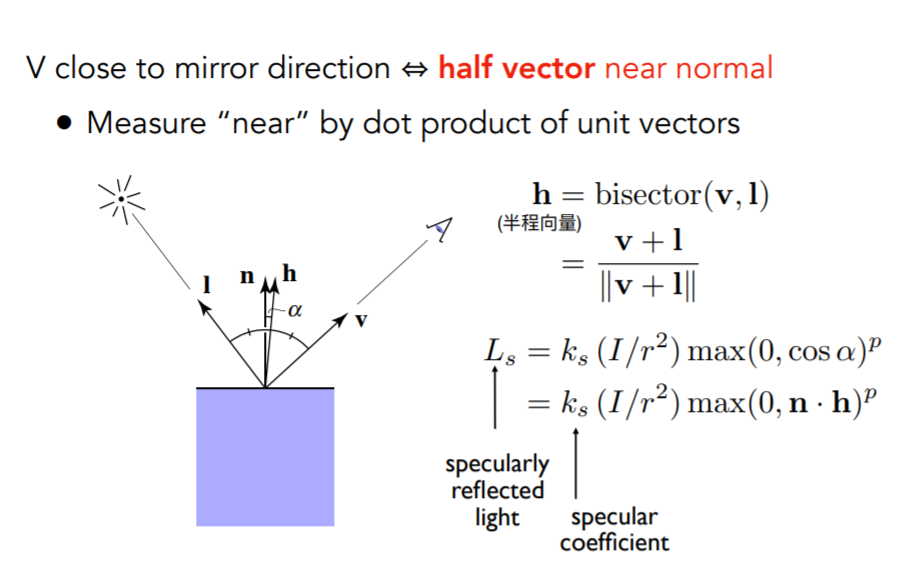
我们用\(\pmb{h}\)和\(\pmb{n}\)的夹角来衡量\(\pmb{R}\)和\(\pmb{v}\)的夹角
然后就会有与漫反射类似的公式

\[L_s=k_s\frac{I}{r^2}\max(0,\pmb{n}*\pmb{h})^p \]

最后一个\(p\)次方的原因是这样的：如果像之前一样\(p=1\)，那么我们偏离\(45°\)时光线只会衰减到原来的\(\frac{\sqrt2}{2}\)倍
但是众所周知，镜面反射的光你偏个很小的角度就基本上看不到了
所以我们要把这个衰减倍数放大，实际操作中一般\(p=100\sim 200\)
3.环境光
极其简化

\[L_a=k_aI_a \]

最后的效果就是这样

L8 Shading2(Shading,Pipeline,Texture Mapping)

三种着色方法：逐面，逐点，逐像素
某点法向量等于其周围面的法向量的（加权）平均
也就是$$N_v=\frac{\sum_{i=1}^{{n}{N_i}}{||\sum_{i=1}}||}$$

---

渲染管线

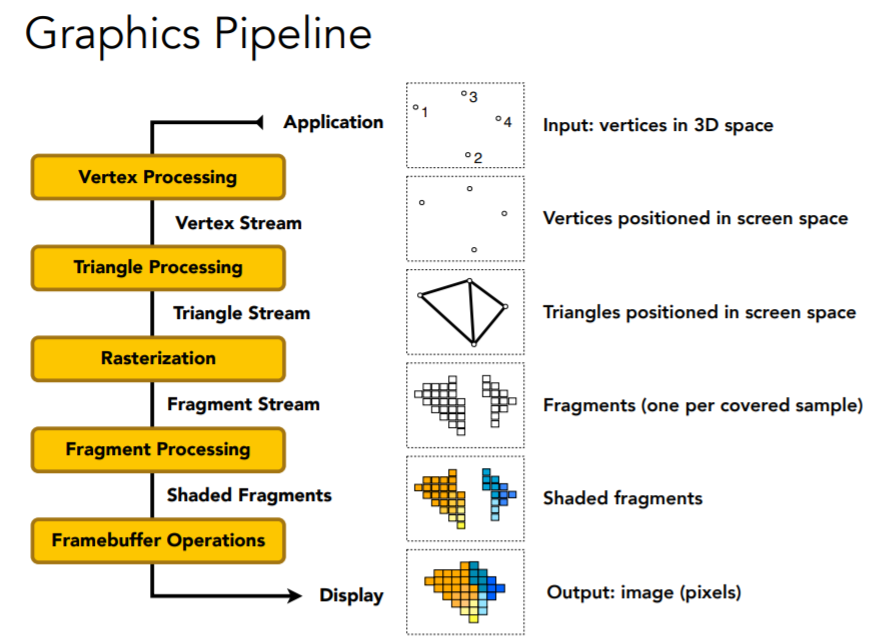
某个在线写渲染器的地方

L9 Shading3(Texture Mapping)

Barycentric Coordinate 重心坐标
用来对三角面片插值的
概念不多说了

\[(x,y)=\alpha A+\beta B+\gamma C\\ \alpha=\frac{-(x-x_b)(y_c-y_b)+(y-y_b)(x_c-x_b)}{-(x_a-x_b)(y_c-y_b)+(y_a-y_b)(x_c-x_b)}\\ \beta=\frac{-(x-x_c)(y_a-y_c)+(y-y_c)(x_a-x_c)}{-(x_b-x_c)(y_a-y_c)+(y_b-y_c)(x_a-x_c)}\\ \gamma=1-\alpha-\beta\]

---

Texture Mapping 纹理映射
流程：对每一个像素点，把\(x-y\)坐标映射到纹理图的\(u-v\)坐标系，把对应点的数据提出来作为自己的数据
问题：这样映射过去很有可能不是整数点
方法：

1. 如果纹理图比较小
   Bilinear/Bicubic插值
   简单讲一下Bilinear(双线性）插值
   其实就是上下两个水平插值，再一个垂直插值（两个垂直再一个水平是一样的）
   公式直接看图
   
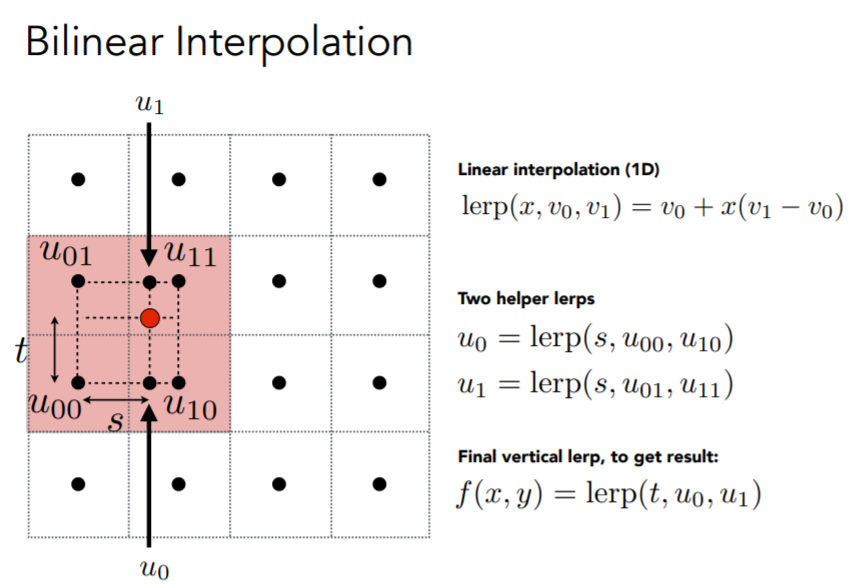
2. 如果纹理图过大
   众所周知，近处的图所占的纹理应该较小，而远处的应该较大
   不理解的话看图吧
   
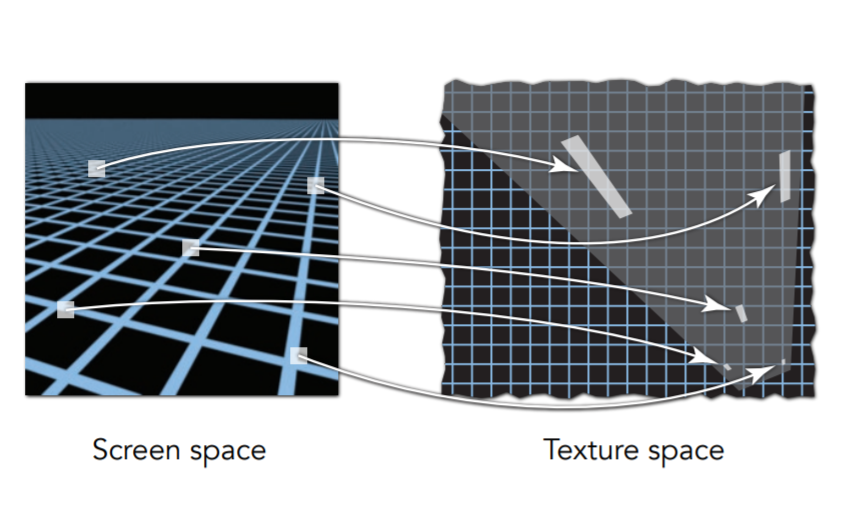
   我们之前的操作是直接取这个点作为这一块的值
   然而如果这样做，远处的点占很大的纹理却直接取其中一点作为整个区域的取值
   相当于高频信号，低频采样
   所以就会出现摩尔纹
   解决办法：
3. Supersampling
   然而这个代价太大了
4. Mipmap
   快，估计，正方形
   大概思路就是倍增，先预处理\(log\)层，再在查询时取\(log\)，如果不是整数就插值，作为其估计值
   也就是三线性插值
   eg：有一张\(128*128\)的图，你就先预处理\(64*64\)，\(32*32\)，...，\(1*1\)的图出来
   然后你要区间查询一张\(96*96\)的图，你就取个\(log\)，再把两层间这个点Bilinear出来的值再插值一遍
   缺点：
   远处的会糊掉，因为这个只能用正方形去拟合
   比如上面那张图，有个很细的区域，那个用正方形拟合显然不太对
5. Anisotropic Filtering（各向异性过滤）
   就是把上面那个正方形换成长方形，查询时是一样的